目录
1.任务安排1
2.任务安排2
3.任务安排3
4.运输小猫
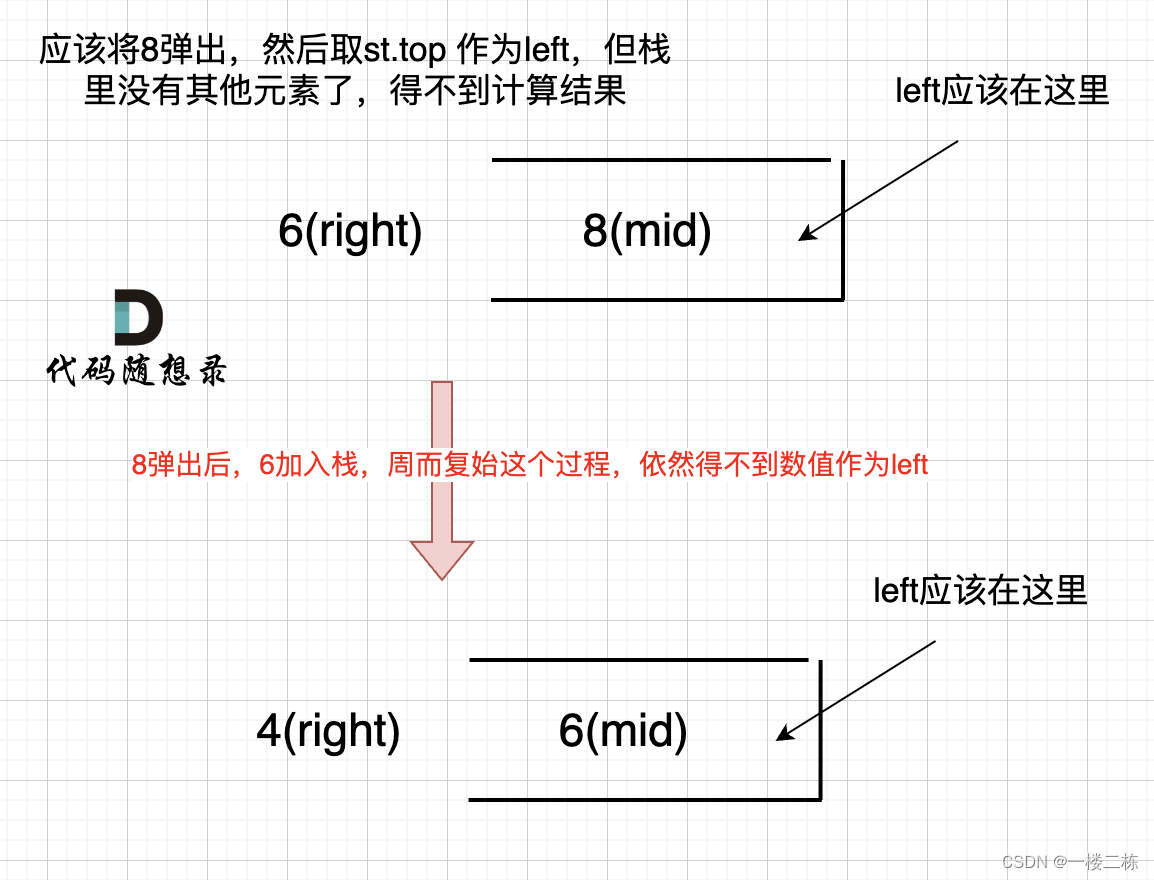
在处理下图的最小截距问题上面,我们该如何在维护的凸包中找到战距最小的点?

相当于在一个单调的队列中,找到第一个大于某一个数的点。
-
斜率单调递增,新加的点的横坐标也单调递增。
-
在查询的时候,可以将队头小于当前斜率的点全部删掉。
-
在插入的时候,将队尾所有不在凸包上的点全部删掉。
-
-
当斜率不再具有单调性,但是新加的点的横坐标一定单调递增。
-
在查询的时候,只能二分来查找
-
在插入的时候,将队尾所有不在鼓包上的点全部删掉。
-
1.任务安排1
300.有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 Ci。
请为机器规划一个分组方案,使得总费用最小。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 5010;
int n, s;
int sumt[N], sumc[N];
int f[N];
int q[N];
int main()
{
scanf("%d%d", &n, &s);
for(int i = 1;i <= n; i++)
{
int t, c;
scanf("%d%d", &t, &c);
sumt[i] = sumt[i - 1] + t;
sumc[i] = sumc[i - 1] + c;
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
for(int i = 1;i <= n; i++)
for(int j = 0;j < i; j++)
f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));
printf("%d\n", f[n]);
return 0;
}但是因为后来是数据加强了,不得不用long long来处理相应的问题。
可以用如下代码处理:
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 5050;
int n, s;
LL st[N], sc[N];
LL f[N];
int main()
{
scanf("%d%d", &n, &s);
for (int i = 1; i <= n; i ++ )
{
scanf("%d%d", &st[i], &sc[i]);
st[i] += st[i - 1], sc[i] += sc[i - 1];
}
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < i; j ++ )
f[i] = min(f[i], f[j] + st[i] * (sc[i] - sc[j]) + s * (sc[n] - sc[j]));
printf("%lld\n", f[n]);
return 0;
}2.任务安排2

301.有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 Ci。
请为机器规划一个分组方案,使得总费用最小。
和上一题相比,就是N的数据域扩张了。
1≤N≤3×105
1≤Ti,Ci≤512
0≤S≤512
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 300010;
int n, s;
LL c[N], t[N];
LL f[N];
LL q[N];
int main()
{
scanf("%d%d", &n, &s);
for(int i = 1;i <= n; i++)
{
scanf("%lld%lld", &t[i], &c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
int hh = 0, tt = 0;
q[0] = 0;
for(int i = 1;i <= n; i++)
{
while(hh < tt && (f[q[hh + 1]] - f[q[hh]]) <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) hh++;
int j = q[hh];
f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];
while(hh < tt && ((f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]])) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt--;
q[++tt] = i;
}
printf("%d\n", f[n]);
return 0;
}3.任务安排3
有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 Ci。
请为机器规划一个分组方案,使得总费用最小。
1≤N≤3×105
0≤S,Ci≤512
−512≤Ti≤512
与任务安排2相比,Ti存在负值。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 300010;
int n, s;
LL t[N], c[N];
LL f[N];
int q[N];
int main()
{
scanf("%d%d", &n, &s);
for(int i = 1;i <= n; i++)
{
scanf("%lld%lld", &t[i], &c[i]);
t[i] += t[i - 1];
c[i] += c[i - 1];
}
int hh = 0, tt = 0;
q[0] = 0;
for(int i = 1;i <= n; i++)
{
int l = hh, r = tt;
while(l < r)
{
int mid = l + r >> 1;
if(f[q[mid + 1]] - f[q[mid]] > (t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) r = mid;
else l = mid + 1;
}
int j = q[r];
f[i] = f[j] - (t[i] + s) * c[j] + t[i] * c[i] + s * c[n];
while(hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt]]) >= (f[i] - f[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt--;
q[++tt] = i;
}
printf("%lld\n", f[n]);
return 0;
}4.运输小猫
303.小 S 是农场主,他养了 M 只猫,雇了 P 位饲养员。
农场中有一条笔直的路,路边有 N 座山,从 1 到 N 编号。
第 ii 座山与第 i−1 座山之间的距离为 Di。
饲养员都住在 1 号山。
有一天,猫出去玩。
第 ii 只猫去 Hi 号山玩,玩到时刻 Ti 停止,然后在原地等饲养员来接。
饲养员们必须回收所有的猫。
每个饲养员沿着路从 1 号山走到 N 号山,把各座山上已经在等待的猫全部接走。
饲养员在路上行走需要时间,速度为 1 米/单位时间。
饲养员在每座山上接猫的时间可以忽略,可以携带的猫的数量为无穷大。
例如有两座相距为 1 的山,一只猫在 2 号山玩,玩到时刻 3 开始等待。
如果饲养员从 1 号山在时刻 2 或 3 出发,那么他可以接到猫,猫的等待时间为 0 或 1。
而如果他于时刻 1 出发,那么他将于时刻 2 经过 2 号山,不能接到当时仍在玩的猫。
你的任务是规划每个饲养员从 1 号山出发的时间,使得所有猫等待时间的总和尽量小。
饲养员出发的时间可以为负。
输入格式
第一行包含三个整数 N,M,P
第二行包含 n−1 个整数,D2,D3,…,DN
接下来 M 行,每行包含两个整数 Hi 和 Ti。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = 1e5 + 10, P = 110;
int n, m, p;
LL d[N], t[N], a[N], s[N];
LL f[P][M];
int q[M];
LL get_y(int k, int j)
{
return f[j - 1][k] + s[k];
}
int main()
{
scanf("%d%d%d", &n, &m, &p);
for(int i = 2;i <= n; i++)
{
scanf("%lld", &d[i]);
d[i] += d[i - 1];
}
for(int i = 1;i <= m; i++)
{
int h;
scanf("%d%lld", &h, &t[i]);
a[i] = t[i] - d[h];
}
sort(a + 1, a + m + 1);
for(int i = 1;i <= m; i++) s[i] = s[i - 1] + a[i];
memset(f, 0x3f, sizeof f);
for(int i = 0;i <= p; i++) f[i][0] = 0;
for(int j = 1;j <= p; j++)
{
int hh = 0, tt = 0;
q[0] = 0;
for(int i = 1;i <= m; i++)
{
while(hh < tt && (get_y(q[hh + 1], j) - get_y(q[hh], j)) <= a[i] * (q[hh + 1] - q[hh])) hh++;
int k = q[hh];
f[j][i] = f[j - 1][k] - a[i] * k + s[k] + a[i] * i - s[i];
while(hh < tt && (get_y(q[tt], j) - get_y(q[tt - 1], j)) * (i - q[tt]) >= (get_y(i, j) - get_y(q[tt], j)) * (q[tt] - q[tt - 1])) tt--;
q[++tt] = i;
}
}
printf("%lld", f[p][m]);
return 0;
}