前面介绍了两种不同的压缩感知实现:
图像压缩感知的MATLAB实现(OMP)
压缩感知的图像仿真(MATLAB源代码)
上述两种方法还存在着“速度慢、精度低”等不足。
本篇介绍一种新的方法。
压缩感知(Compressed Sensing)是一种信号处理技术,旨在通过取样和重构过程中的稀疏性或低维性的先验知识,从少量的测量数据中恢复原始信号。与传统的信号采样方式相比,压缩感知可以以更低的采样率获取信号,并在一定程度上保持较高的重构质量。
以下是压缩感知的一些重要知识点:
-
稀疏性:压缩感知假设信号在某个表示域下是稀疏的,即信号能够用较少的非零系数表示。这意味着信号的大部分能量集中在少数几个基函数上,而其他系数很接近于零。
-
测量矩阵:压缩感知使用一个测量矩阵来计算信号的投影测量。测量矩阵可以是随机矩阵或基于不同的测量方法生成的。测量矩阵的选择对于压缩感知的性能具有重要影响。
-
重构算法:压缩感知利用稀疏表示的先验知识,通过最小化正则化函数来恢复原始信号。常用的重构算法包括基于L1范数的贪婪迭代算法(如OMP、CoSaMP)、基于迭代阈值的算法(如IST、FISTA)和基于凸优化的算法(如基于内点法的L1优化)。
-
重构性能:压缩感知的重构性能用于衡量在给定的测量数量下,重构的信号与原始信号之间的误差。重构性能受到信号的稀疏度、测量矩阵的设计和重构算法的选择等因素的影响。
MATLAB和其他数学软件提供了用于压缩感知的工具箱和函数,如 l1magic 和 SPGL1。这些函数可以用于生成测量矩阵、实现重构算法,并进行压缩感知的仿真和实验。
压缩感知在图像处理、语音信号处理、雷达成像、医学成像等领域都得到了广泛的应用。它提供了一种新的思路和方法,可以在低采样率下实现高质量的信号重构,并对传统信号采样理论进行了一定的突破。
MATLAB实现
针对网络上沙威老师的代码中所使用小波变换进行了修改。
将其中自定义的dwt函数修改了了使用MATLAB自带的dwt2函数。
MATLAB代码
MATLAB代码实现如下:
clc;clear
% 读文件
X=imread('lenagray.bmp');
X=double(X);
[a,b]=size(X);
% % 小波变换矩阵生成
% ww=DWT(a);
% % ww=a;
% %
% % % 小波变换让图像稀疏化(注意该步骤会耗费时间,但是会增大稀疏度)
% X1=ww*sparse(X)*ww';
% % % X1=X;
% X1=full(X1);
%
% X1=X;
[LL1, LH1, HL1, HH1] = dwt2(X, 'haar');
[LL2, LH2, HL2, HH2] = dwt2(LL1, 'haar');
[LL3, LH3, HL3, HH3] = dwt2(LL2, 'haar');
[LL4, LH4, HL4, HH4] = dwt2(LL3, 'haar');
LL3 = [LL4, LH4; HL4, HH4];
LL2=[LL3, LH3; HL3, HH3];
LL1=[LL2, LH2; HL2, HH2];
X1=[LL1, LH1; HL1, HH1];
% 随机矩阵生成
M=190;
R=randn(M,a);
% R=mapminmax(R,0,255);
% R=round(R);
% 测量值
Y=R*X1;
% OMP算法
% 恢复矩阵
X2=zeros(a,b);
% 按列循环
for i=1:b
% 通过OMP,返回每一列信号对应的恢复值(小波域)
rec=omp(Y(:,i),R,a);
% 恢复值矩阵,用于反变换
X2(:,i)=rec;
end
% 原始图像
figure(1);
imshow(uint8(X));
title('原始图像');
% 变换图像
figure(2);
imshow(uint8(X1));
title('小波变换后的图像');
% 压缩传感恢复的图像
figure(3);
% 小波反变换
% X3=ww'*sparse(X2)*ww;
% X3=X2;
% X3=full(X3);
% X3=idwt2(X2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 执行逆小波变换
[LL1, LH1, HL1, HH1] = partitionMatrix(X2);
[LL2, LH2, HL2, HH2] = partitionMatrix(LL1);
[LL3, LH3, HL3, HH3] = partitionMatrix(LL2);
[LL4, LH4, HL4, HH4] = partitionMatrix(LL3);
% 第四级逆变换
LL3 = idwt2(LL4, LH4, HL4, HH4, 'haar');
% 第三级逆变换
LL2= idwt2(LL3, LH3, HL3, HH3, 'haar');
% 第二级逆变换
LL1 = idwt2(LL2, LH2, HL2, HH2, 'haar');
% 第一级逆变换,得到原始图像
X3 = idwt2(LL1, LH1, HL1, HH1, 'haar');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
imshow(uint8(X3));
title('恢复的图像');
% 误差(PSNR)
% MSE误差
errorx=sum(sum(abs(X3-X).^2));
% PSNR
psnr=10*log10(255*255/(errorx/a/b))
% OMP的函数
% s-测量;T-观测矩阵;N-向量大小
function hat_y=omp(s,T,N)
Size=size(T); % 观测矩阵大小
M=Size(1); % 测量
hat_y=zeros(1,N); % 待重构的谱域(变换域)向量
Aug_t=[]; % 增量矩阵(初始值为空矩阵)
r_n=s; % 残差值
for times=1:M; % 迭代次数(稀疏度是测量的1/4)
for col=1:N; % 恢复矩阵的所有列向量
product(col)=abs(T(:,col)'*r_n); % 恢复矩阵的列向量和残差的投影系数(内积值)
end
[val,pos]=max(product); % 最大投影系数对应的位置
Aug_t=[Aug_t,T(:,pos)]; % 矩阵扩充
T(:,pos)=zeros(M,1); % 选中的列置零(实质上应该去掉,为了简单我把它置零)
aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s; % 最小二乘,使残差最小
r_n=s-Aug_t*aug_y; % 残差
pos_array(times)=pos; % 纪录最大投影系数的位置
if (norm(r_n)<0.9) % 残差足够小
break;
end
end
hat_y(pos_array)=aug_y; % 重构的向量
end
function [X1, X2, X3, X4] = partitionMatrix(X)
% 获取矩阵X的大小
[m, n] = size(X);
% 将矩阵X划分为四等份
X1 = X(1:m/2, 1:n/2); % 左上角子矩阵
X2 = X(1:m/2, n/2+1:end); % 右上角子矩阵
X3 = X(m/2+1:end, 1:n/2); % 左下角子矩阵
X4 = X(m/2+1:end, n/2+1:end); % 右下角子矩阵
end
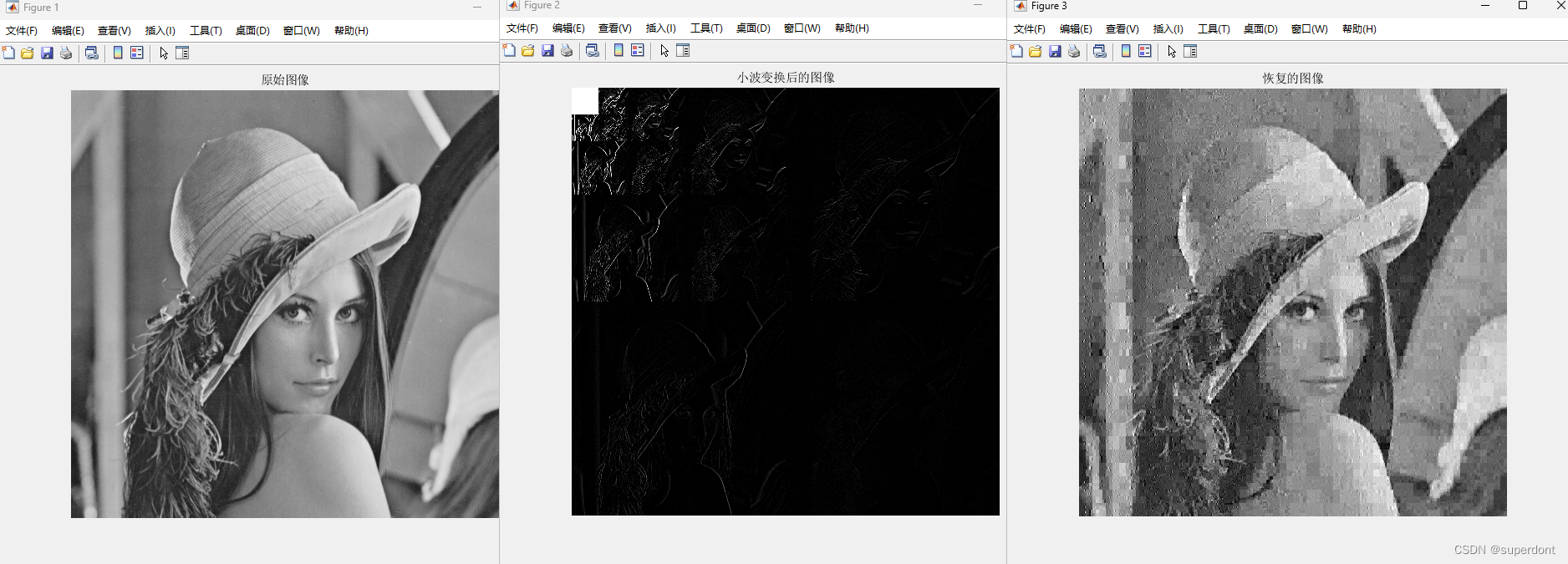
输出结果
输出结果如下,效果一般,而且速度较慢。
参考知识点
MATLAB小波变换函数
小波变换是一种信号处理技术,通过在时间-频率域中使用基于小波的函数进行信号分析。小波变换在处理非平稳信号和图像时特别有用,可以将信号分解为不同频率的成分。它在数据压缩、去噪、特征提取等领域有广泛应用。
MATLAB中提供了用于二维离散小波变换的函数 dwt2,可以将图像进行小波分解。该函数执行的是多级离散小波变换,将图像分解为多个尺度的近似系数和细节系数。具体来说,dwt2函数的语法如下:
[C, S] = dwt2(X, wavelet)
其中,
X是输入的二维图像;wavelet是指定的小波基函数,比如'haar'、'db1'等;C是包含小波变换系数的矩阵;S是描述小波变换结果各层的结构体。
你可以通过调用dwt2函数来执行二维离散小波变换,得到图像的小波分解系数和结构信息。然后,你可以进一步对获得的系数进行处理,比如重构原始图像、进行图像压缩、图像增强等。
需要注意的是,小波变换是一种复杂的信号处理技术,需要一定的理论基础和实践经验来使用和理解。
自定义函数
网络上沙威老师的dwt版本如下:
function ww=DWT(N)
[h,g]=wfilters('haar','d'); % 分解低通和高通滤波器
% N=256; % 矩阵维数(大小为2的整数幂次)
L=length(h); % 滤波器长度
rank_max=log2(N); % 最大层数
rank_min=double(int8(log2(L)))+1+3; % 最小层数
ww=1; % 预处理矩阵
% 矩阵构造
for jj=rank_min:rank_max
nn=2^jj;
% 构造向量
p1_0=sparse([h,zeros(1,nn-L)]);
p2_0=sparse([g,zeros(1,nn-L)]);
% 向量圆周移位
for ii=1:nn/2
p1(ii,:)=circshift(p1_0',2*(ii-1))';
p2(ii,:)=circshift(p2_0',2*(ii-1))';
end
% 构造正交矩阵
w1=[p1;p2];
mm=2^rank_max-length(w1);
w=sparse([w1,zeros(length(w1),mm);zeros(mm,length(w1)),eye(mm,mm)]);
ww=ww*w;
clear p1;clear p2;
end
相关博文
理解并实现OpenCV中的图像平滑技术
OpenCV中的边缘检测技术及实现
OpenCV识别人脸案例实战
入门OpenCV:图像阈值处理
我的图书
下面两本书欢迎大家参考学习。
OpenCV轻松入门
李立宗,OpenCV轻松入门,电子工业出版社,2023
本书基于面向 Python 的 OpenCV(OpenCV for Python),介绍了图像处理的方方面面。本书以 OpenCV 官方文档的知识脉络为主线,并对细节进行补充和说明。书中不仅介绍了 OpenCV 函数的使用方法,还介绍了函数实现的算法原理。
在介绍 OpenCV 函数的使用方法时,提供了大量的程序示例,并以循序渐进的方式展开。首先,直观地展示函数在易于观察的小数组上的使用方法、处理过程、运行结果,方便读者更深入地理解函数的原理、使用方法、运行机制、处理结果。在此基础上,进一步介绍如何更好地使用函数处理图像。在介绍具体的算法原理时,本书尽量使用通俗易懂的语言和贴近生活的实例来说明问题,避免使用过多复杂抽象的公式。
本书适合计算机视觉领域的初学者阅读,包括在校学生、教师、专业技术人员、图像处理爱好者。
本书第1版出版后,深受广大读者朋友的喜爱,被很多高校选为教材,目前已经累计重印9次。为了更好地方便大家学习,对本书进行了修订。

计算机视觉40例
李立宗,计算机视觉40例,电子工业出版社,2022
近年来,我深耕计算机视觉领域的课程研发工作,在该领域尤其是OpenCV-Python方面积累了一点儿经验。因此,我经常会收到该领域相关知识点的咨询,内容涵盖图像处理的基础知识、OpenCV工具的使用、深度学习的具体应用等多个方面。为了更好地把所积累的知识以图文的形式分享给大家,我将该领域内的知识点进行了系统的整理,编写了本书。希望本书的内容能够对大家在计算机视觉方向的学习有所帮助。
本书以OpenCV-Python(the Python API for OpenCV)为工具,以案例为载体,系统介绍了计算机视觉从入门到深度学习的相关知识点。
本书从计算机视觉基础、经典案例、机器学习、深度学习、人脸识别应用等五个方面对计算机视觉的相关知识点做了全面、系统、深入的介绍。书中共介绍了40余个经典的计算机视觉案例,其中既有字符识别、信息加密、指纹识别、车牌识别、次品检测等计算机视觉的经典案例,也包含图像分类、目标检测、语义分割、实例分割、风格迁移、姿势识别等基于深度学习的计算机视觉案例,还包括表情识别、驾驶员疲劳监测、易容术、识别年龄和性别等针对人脸的应用案例。
在介绍具体的算法原理时,本书尽量使用通俗易懂的语言和贴近生活的示例来说明问题,避免使用复杂抽象的公式来介绍。
本书适合计算机视觉领域的初学者阅读,适于在校学生、教师、专业技术人员、图像处理爱好者使用。












![P1450 [HAOI2008] 硬币购物 dp 容斥 —— s - c[i]*(d[i]+1)怎么理解](https://img-blog.csdnimg.cn/direct/827fd5afe0104237bc75fbb688247b0b.png)