动态规划

  如果问题是由重叠的子问题构成的，那就可以用动态规划（dynamic programming）来解决它。

  在求解动态规划问题的时候，我们需要思考以下5个步骤：

1. 状态表示（这是最重要的）：我们会创建一个dp表，将较小问题的解放在表中，这样我们就会得到原始问题的解，所以状态表示就是清楚dp表里面某个位置所表示的含义。
2. 状态转移方程（最难的）：也就是从题干中找到关于dp[i]的等式。
3. 初始化：填表时，保证不越界。当求解问题时，需要知道较小问题的解，较小问题的解一定也是通过更小问题的解求得的，所以我们必须知道最初问题的解，以此来求得较大问题的解，这就需要我们限定dp[i]中i的取值范围。
4. 填表顺序：当我们求解当前问题时，需要知道所需较小子问题的解，这就需要我们先求解得到较小子问题的解，这就是填表顺序。
5. 返回值：题目要求+状态表示

  在代码中的体现为四个步骤：1. 创建dp表。 2. 初始化。 3. 填表。 4. 返回。

LeetCode题目

第 N 个泰波那契数

1137. 第 N 个泰波那契数

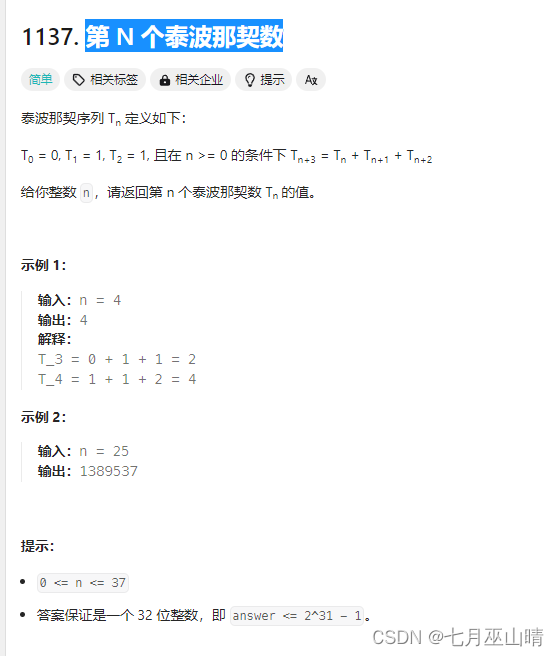
求解1

class Solution {
public:
    int tribonacci(int n) {

        // 处理边界问题
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;
        // 1. 创建dp数组
        vector<int> dp(n+1);
        // 2. 初始化
        dp[0] = 0, dp[1] = dp[2] = 1;
        // 3. 填表
        for(int i = 3; i <= n; i++)
        {
            dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
        }
        // 4. 返回
        return dp[n];
    }
};

求解2（滚动数组）

  上面的求解1的空间复杂度时O(N)。

  通过上图我们容易看出来，每次求解的时候，我们只需要知道前面的三个值即可，但是求解1中我们使用了一个数组，这就浪费了我们得空间，我们优化就可以从这方面入手。
  定义四个变量，前三个变量表示dp[i-1], dp[i-2],dp[i-3]。第四个变量表示前三个变量相加的值，也就是dp[i]。每次需要求解下一个值的时候，就平移这前三个变量。

class Solution {
public:
    int tribonacci(int n) {
        // 1.创建dp表
        // 2.初始化
        int a = 0, b = 1, c = 1, d = 2;
        
        // 解决边界问题
        if(0 == n) return 0;
        if(1 == n || 2 == n) return 1;

        // 3.填表
        for(int i = 3; i <= n; i++)
        {
            d = a+b+c;
            a=b, b=c, c=d;
        }

        return d;
    }
};

三步问题

三步问题

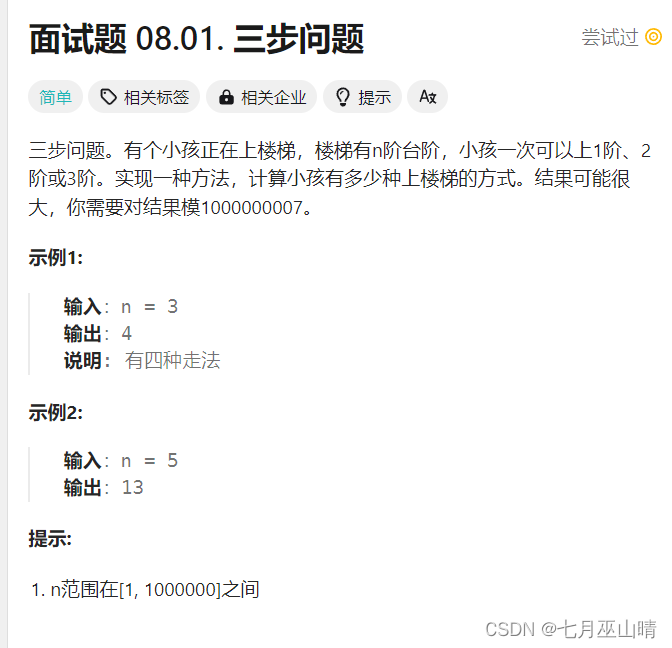
  我们可以尝试手动求解前面几个的解，填入dp表。

  当我们计算到第4个台阶的时候，我们发现可以直接到达第4个台阶的方式分别是：

1. 从第3个台阶起，上1个台阶到达。
2. 从第2个台阶起，上2个台阶到达。
3. 从第1个台阶起，上3个台阶到达。

  因为小孩一次只可以上1阶、2阶或3阶，所以只有这3种方式可以直接到达第4个台阶。
则我们经过第3个台阶到达第4个台阶的方式数有4种。
   经过第2个台阶到达第4个台阶的方式数有2种。
   经过第1个台阶到达第4个台阶的方式数有1种。
将三种方式相加，就是总的到达第4个台阶的方式数7种。
  按照这个方法往下求解，发现依旧适用。

于是简化理解，
       状态表示为：dp[i]表示到达第i个台阶的方式数量。
     状态转移方程为：dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
        初始化为：dp[1] = 1, dp[2] = 2, dp[3] = 4;

求解1

class Solution {
public:
    int waysToStep(int n) {
        // 解决边界问题
        if(1 == n || 2 == n) return n;
        if(3 == n) return 4;
        
        // 1.创建dp表
        vector<int> dp(n+1);

        // 2. 初始化
        dp[1] = 1, dp[2] = 2, dp[3] = 4;
        
        // 3. 填表
        for(int i = 4; i <= n; i++)
        {
            dp[i] = ((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;
        }

        return dp[n] ;
    }
};

求解2（滚动数组）

class Solution {
public:
    int waysToStep(int n) {
        // 解决边界问题
        if(1 == n || 2 == n) return n;
        if(3 == n) return 4;
        
        // 1.创建dp表
        // 2. 初始化
        int a = 1, b = 2, c = 4, d = 0;
        
        // 3. 填表
        for(int i = 4; i <= n; i++)
        {
            d = ((a+b)%1000000007+c)%1000000007;
            a=b, b=c, c=d;
        }

        return d ;
    }
};

---

     😄 创作不易，你的点赞和关注都是对我莫大的鼓励，再次感谢您的观看😄