1 N皇后问题(N Queen Problem)
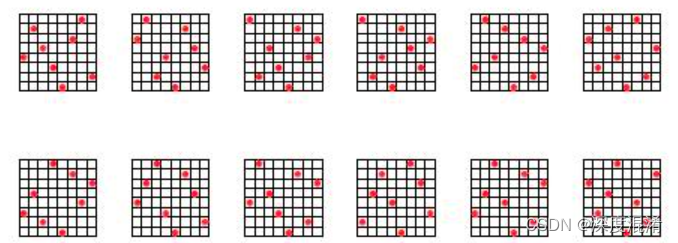
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。

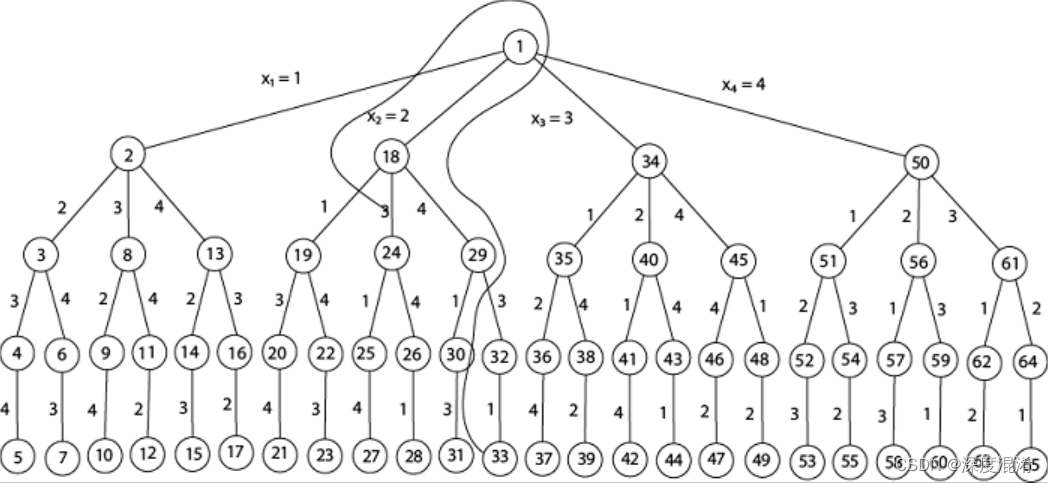
2 回溯算法
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
回溯法也称试探法,它的基本思想是:从问题的某一种状态(初始状态)出发,搜索从这种状态出发所能达到的所有“状态”,当一条路走到“尽头”的时候(不能再前进),再后退一步或若干步,从另一种可能“状态”出发,继续搜索,直到所有的“路径”(状态)都试探过。这种不断“前进”、不断“回溯”寻找解的方法,就称作“回溯法”。
3 源程序
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// N皇后问题
/// </summary>
public static partial class Algorithm_Gallery
{
private static bool NQP_IsSafe(int[,] board, int row, int col)
{
int N = board.GetLength(0);
for (int i = 0; i < col; i++)
{
if (board[row, i] == 1)
{
return false;
}
}
for (int i = row, j = col; i >= 0 && j >= 0; i--, j--)
{
if (board[i, j] == 1)
{
return false;
}
}
for (int i = row, j = col; j >= 0 && i < N; i++, j--)
{
if (board[i, j] == 1)
{
return false;
}
}
return true;
}
private static bool NQP_Utility(ref int[,] board, int col)
{
int N = board.GetLength(0);
if (col >= N)
{
return true;
}
for (int i = 0; i < N; i++)
{
if (NQP_IsSafe(board, i, col))
{
board[i, col] = 1;
if (NQP_Utility(ref board, col + 1) == true)
{
return true;
}
board[i, col] = 0;
}
}
return false;
}
public static bool NQP_Solve(int n,out int[,] board)
{
board = new int[n, n];
if (NQP_Utility(ref board, 0) == false)
{
return false;
}
return true;
}
public static string ToHtml(int[,] board)
{
int N = board.GetLength(0);
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine("td { padding:5px;text-align:center; }");
sb.AppendLine("</style>");
sb.AppendLine("<table border=1 bordercolor='#999999' style='border-collapse:collapse;'>");
for (int i = 0; i < N; i++)
{
sb.AppendLine("<tr>");
for (int j = 0; j < N; j++)
{
sb.AppendLine("<td>" + board[i, j] + "</td>");
}
sb.AppendLine("</tr>");
}
sb.AppendLine("</table>");
return sb.ToString();
}
}
}
————————————————————————————————
POWER BY 315SOFT.COM
4 源代码
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// N皇后问题
/// </summary>
public static partial class Algorithm_Gallery
{
private static bool NQP_IsSafe(int[,] board, int row, int col)
{
int N = board.GetLength(0);
for (int i = 0; i < col; i++)
{
if (board[row, i] == 1)
{
return false;
}
}
for (int i = row, j = col; i >= 0 && j >= 0; i--, j--)
{
if (board[i, j] == 1)
{
return false;
}
}
for (int i = row, j = col; j >= 0 && i < N; i++, j--)
{
if (board[i, j] == 1)
{
return false;
}
}
return true;
}
private static bool NQP_Utility(ref int[,] board, int col)
{
int N = board.GetLength(0);
if (col >= N)
{
return true;
}
for (int i = 0; i < N; i++)
{
if (NQP_IsSafe(board, i, col))
{
board[i, col] = 1;
if (NQP_Utility(ref board, col + 1) == true)
{
return true;
}
board[i, col] = 0;
}
}
return false;
}
public static bool NQP_Solve(int n,out int[,] board)
{
board = new int[n, n];
if (NQP_Utility(ref board, 0) == false)
{
return false;
}
return true;
}
public static string ToHtml(int[,] board)
{
int N = board.GetLength(0);
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>");
sb.AppendLine("td { padding:5px;text-align:center; }");
sb.AppendLine("</style>");
sb.AppendLine("<table border=1 bordercolor='#999999' style='border-collapse:collapse;'>");
for (int i = 0; i < N; i++)
{
sb.AppendLine("<tr>");
for (int j = 0; j < N; j++)
{
sb.AppendLine("<td>" + board[i, j] + "</td>");
}
sb.AppendLine("</tr>");
}
sb.AppendLine("</table>");
return sb.ToString();
}
}
}