矢量这个词，我们在数学上并不陌生，它是既有方向又有大小的量。而在GIS中，常常利用欧氏空间的点、线、面来表示地理实体，进而构成我们使用频繁的矢量数据，它和栅格数据一同构成了地理信息数据的基础。今天开始，我们会一一给大家介绍矢量数据，矢量数据集合，栅格数据，栅格数据集合在GEE上的访问、常见的操作命令等知识。今天要分享的feature，是带有属性特征的几何图形。

1.feature数据的定义

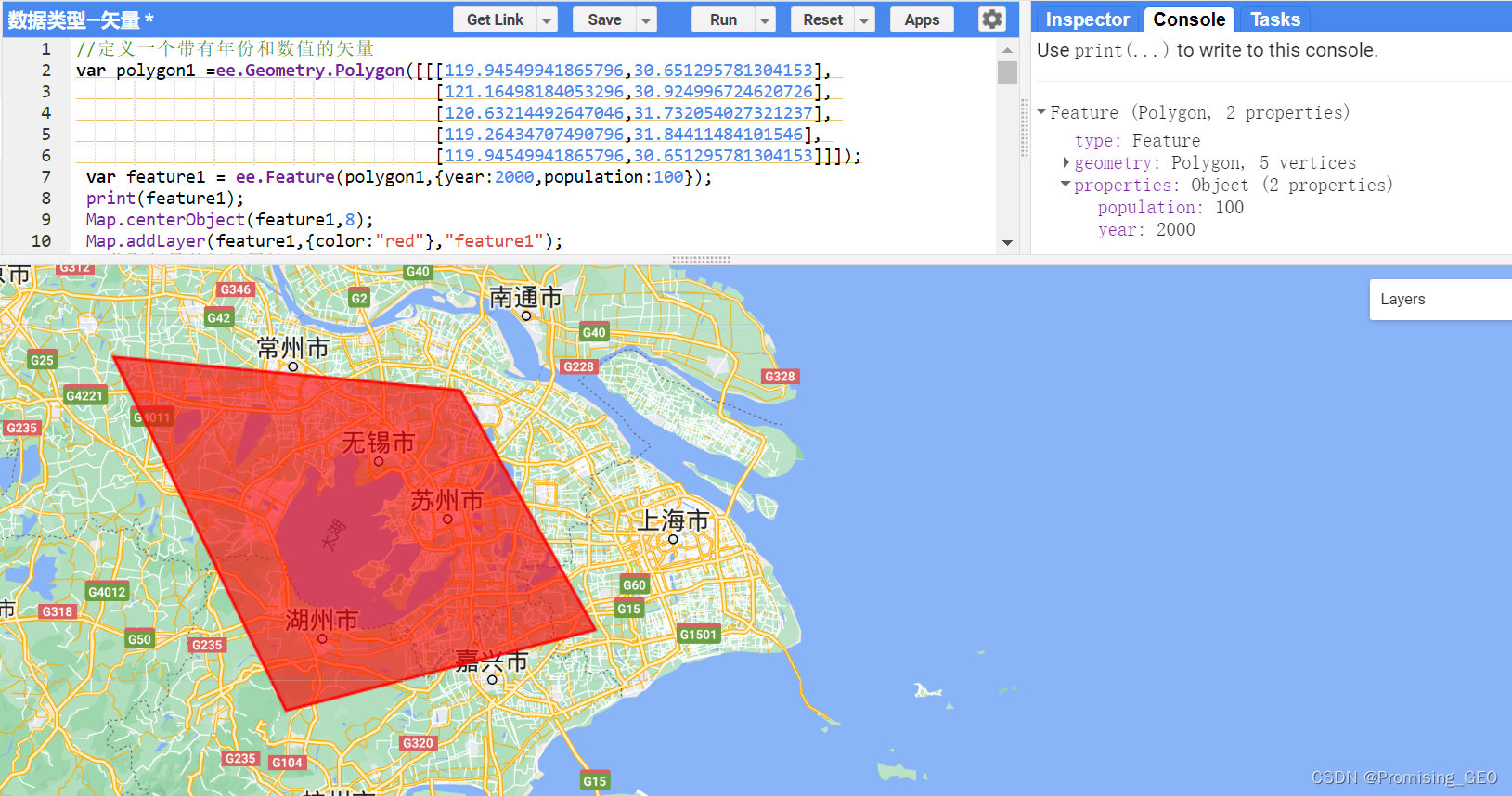
//定义一个带有年份和数值的矢量
var polygon1 =ee.Geometry.Polygon([[[119.94549941865796,30.651295781304153],
                                    [121.16498184053296,30.924996724620726],
                                    [120.63214492647046,31.732054027321237],
                                    [119.26434707490796,31.84411484101546],
                                    [119.94549941865796,30.651295781304153]]]);
 var feature1 = ee.Feature(polygon1,{year:2000,count:100});
 print(feature1);
 Map.centerObject(feature1,8);
 Map.addLayer(feature1,{color:"red"},"feature1");

数据的定义依托于前面讲过的地理几何（http://t.csdnimg.cn/d7RVQ），通过对原有的几何边界进行属性上的编辑，便能给形成能够反映一定信息的矢量数据。此处小编首先定义了一个多边形，接着通过ee.Feature方法进行数据类型的定义，同时给该几何图形增加了年份信息和人口信息（在定义时即可添加），是不是很简单就实现了对矢量数据的定义。

2.对矢量数据的属性进行相关操作

 //获取矢量数据的属性
 print("Year",feature1.get("year"));
 print("Count",feature1.get("population"));
 //设置新的属性
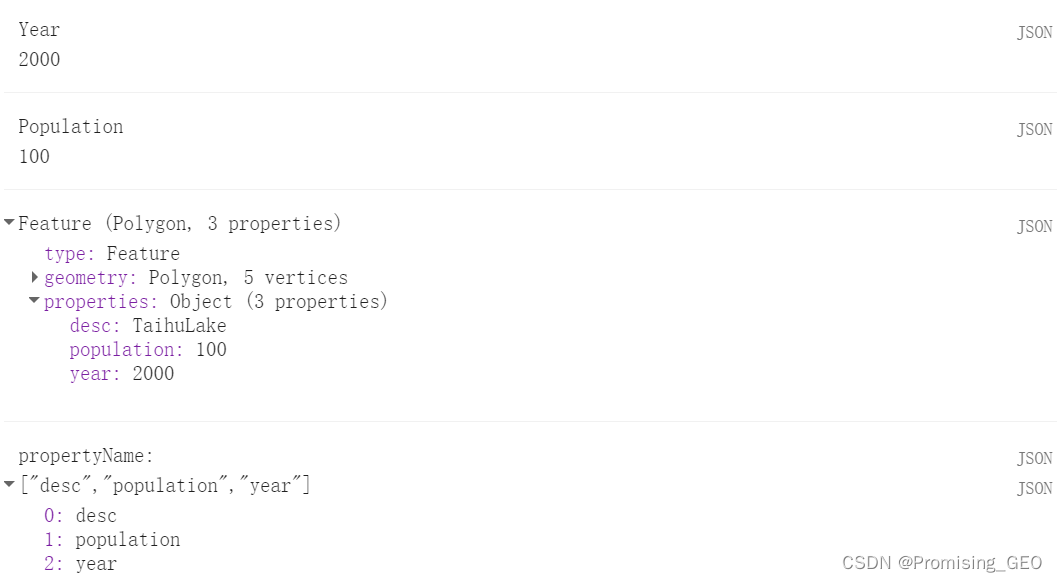
 feature1 = feature1.set("desc","TaihuLake");
 print(feature1);
 //查看所有的数据属性名称
 print("propertyName:",feature1.propertyNames());

要获取矢量数据的属性，使用get(“name”)，设置新的属性，使用set(“propertyname","value")，想查看数据的所有属性名称，使用propertyNames比较合适。

接下来我们要重点聊聊select方法，select方法使用后，会根据括号中指定的属性关键字进行数据的重新生成，当然生成的自然是你想要的只包含该属性的矢量数据啦。而如果想要对其中的某个属性名称进行修改，比如小编在这里看不惯year，想用Date表示日期，我们可以在select中传递两个参数，前面的参数写上原有的名称，后面的参数写上要修改后的名称，注意必须是一一对应的，且参数间用方括号隔开，如下所示：

 //筛选包含特定属性的矢量数据/筛选并修改属性名称
 print(ee.Feature(feature1.select(["count"])));
 var feature2 = feature1.select(["year","population","desc"],
                                ["date","population","desc"]);
feature2 = ee.Feature(feature2);
print(feature2);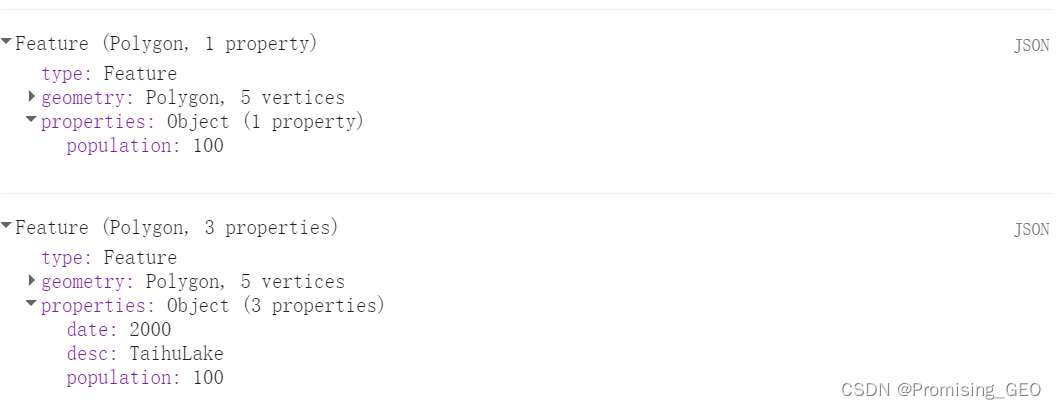

3.空间操作方法

（1）重新定义两个矢量数据

//属性数据空间操作方法
//定义两个面状地物
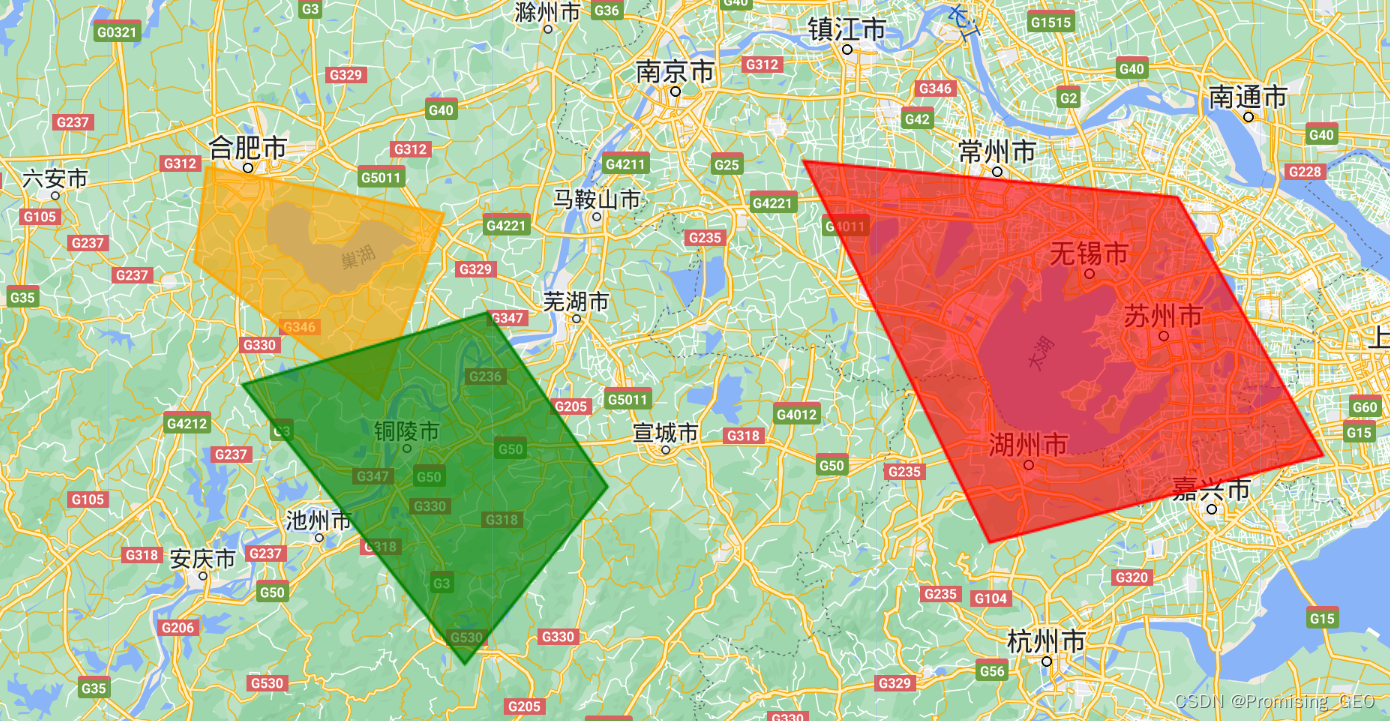
var polygon2 = ee.Geometry.Polygon([[[117.03488606835816,31.530418772379406],
                                     [117.70505208398316,31.098668414373755],
                                     [117.94675130273316,31.6801278448436],
                                     [117.07883138085816,31.824928675333382],
                                     [117.03488606835816,31.530418772379406]]]);
var polygon3 = ee.Geometry.Polygon([[[118.02365559960816,30.267231511702718],
                                     [118.54550618554566,30.825463762625528],
                                     [118.10605306054566,31.371089507224852],
                                     [117.21066731835816,31.145693579861263],
                                     [118.02365559960816,30.267231511702718]]]);
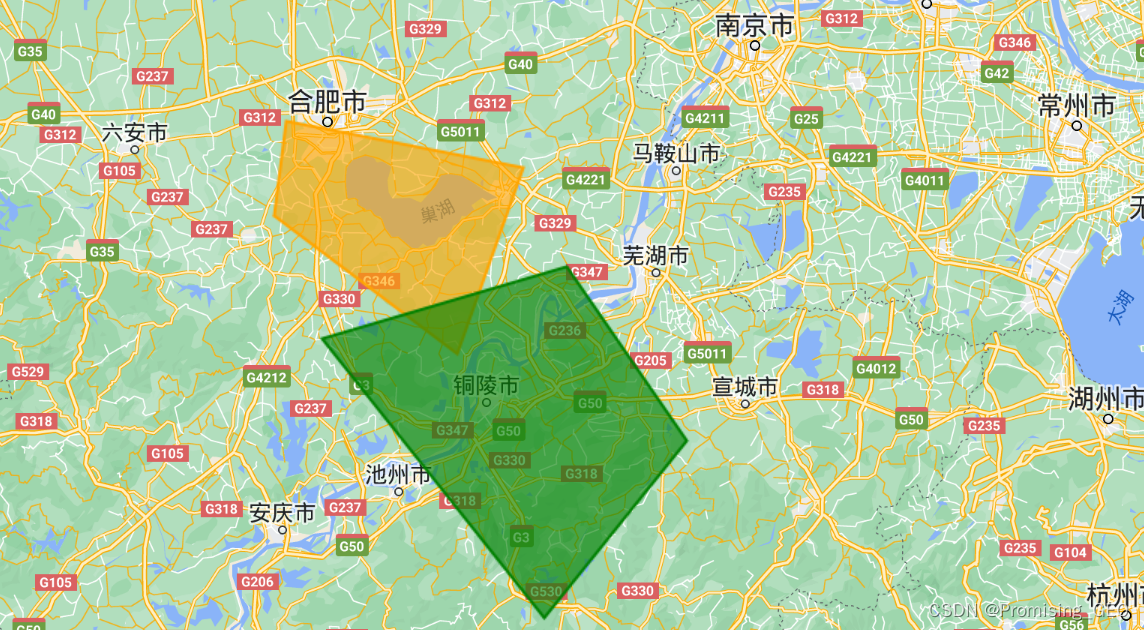
var feature3 = ee.Feature(polygon2);
var feature4 = ee.Feature(polygon3);
Map.centerObject(feature3,8);
Map.addLayer(feature3,{color:"orange"},"feature3");
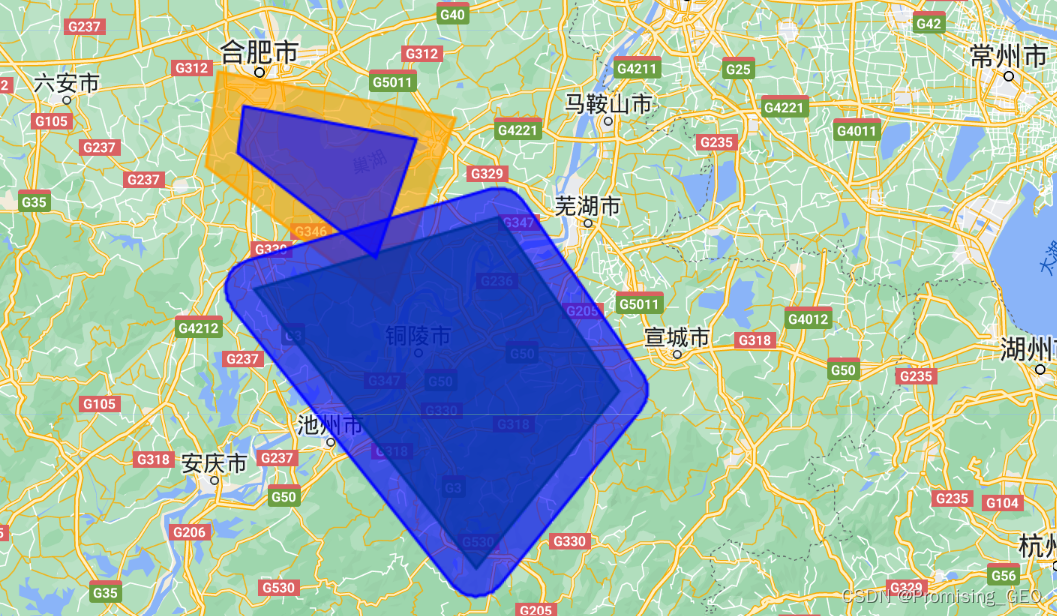
Map.addLayer(feature4,{color:"green"},"feature4");

它们长这样：

（2）求两个范围的面积和周长

//计算地物面积与周长
print("Area1:",feature3.area());
print("Area2:",feature4.area());
print("perimeter1:",feature3.perimeter());
print("perimeter2:",feature4.perimeter());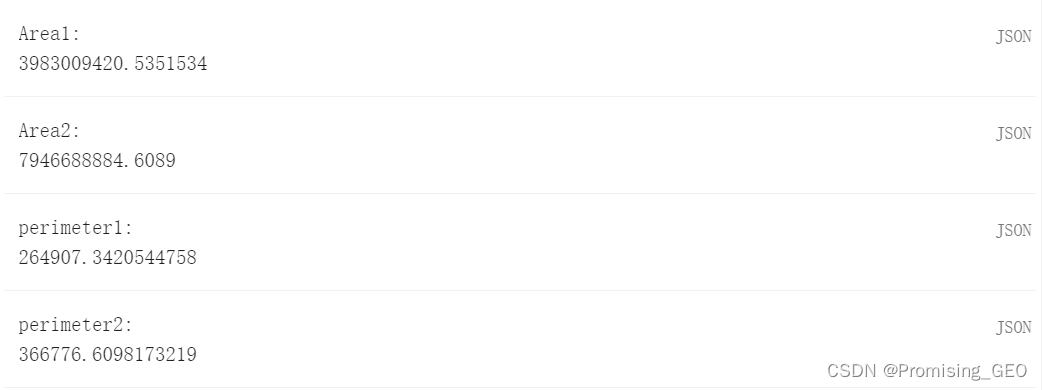

(2)绘制外接矩形

//绘制外接矩形
var Bound1 = feature3.bounds();
var Bound2 = feature4.bounds();
Map.addLayer(Bound1,{"color":"black"},"Bound1");
Map.addLayer(Bound2,{"color":"black"},"Bound2");

外接矩形使用bounds进行绘制，一般沿矩形的顶点延申得到最小的外接矩形。

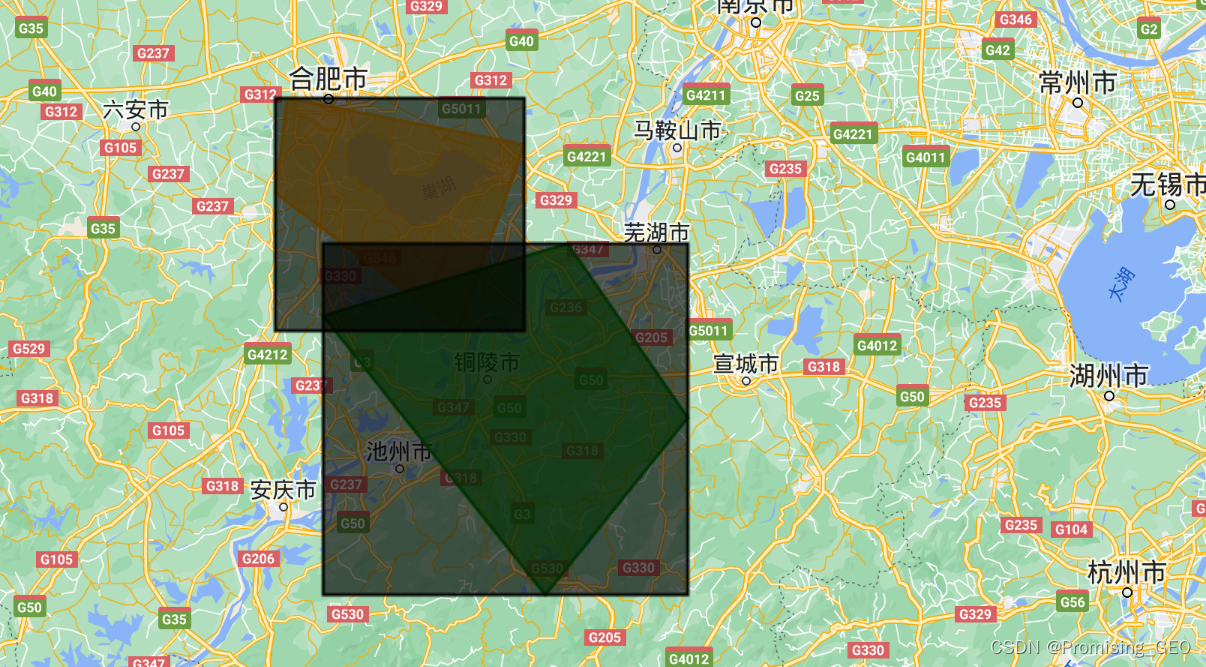
（3）形成中心点

//绘制中心点
var centroid1 = feature3.centroid();
var centroid2 = feature4.centroid();
Map.addLayer(centroid1,{},"C1");
Map.addLayer(centroid2,{},"C2");
print("Centroid1:",centroid1);
print("Centroid2:",centroid2);

中心点，即所在的矢量数据的几何中心位置，一般以坐标的形式给出：

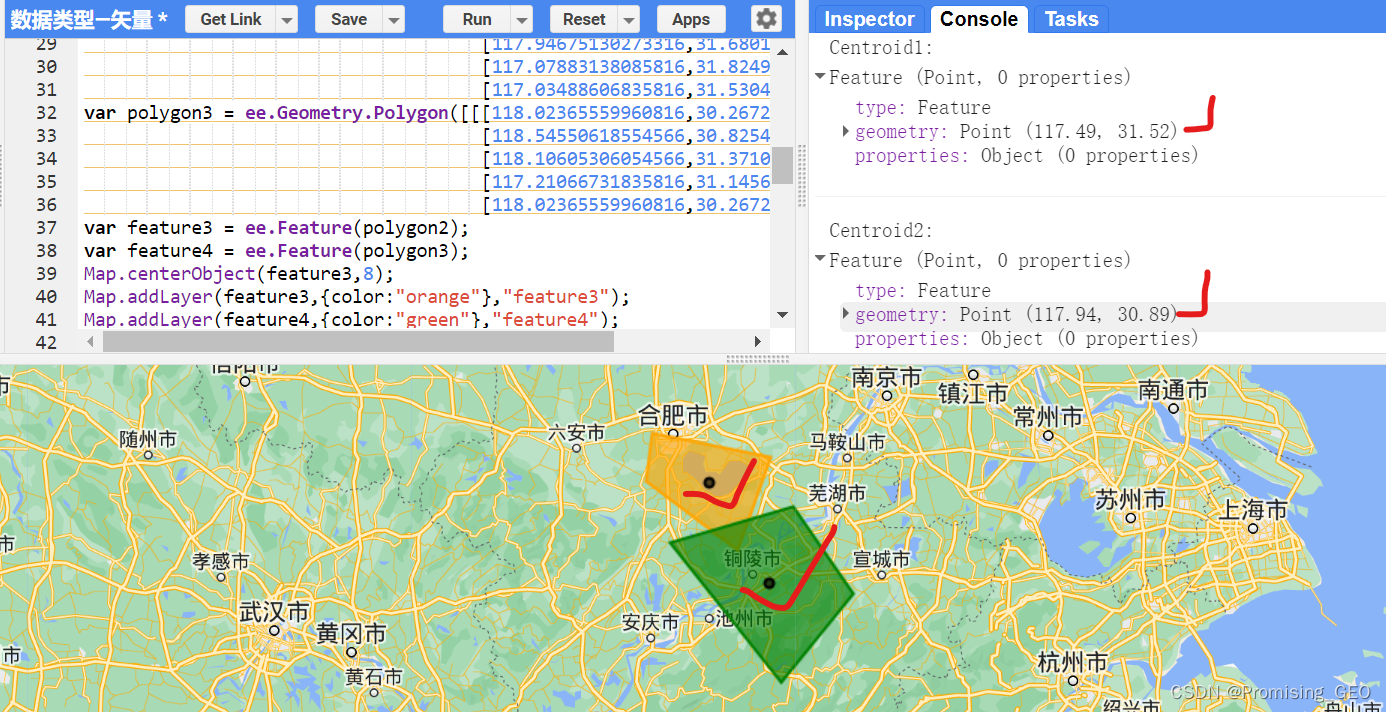
(4）获取几何边界

当我们在获取特定信息比如边界点的坐标信息或者进行数据转换时，有时要把数据的原始的几何边界提取出来，这将用到以下代码：

//获取特定的几何图形
var Geometry1 = feature3.geometry();
var Geometry2 = feature4.geometry();
print("Geometry1:",Geometry1);
print("Geometry2:",Geometry2);
print("Geometry1:",Geometry1.coordinates());
print("Geometry1:",Geometry2.coordinates());

此处小编获取了原始数据的几何图形进行提取，并顺势统计了边界点的坐标，结果将以列表的形式进行返回，如下所示：

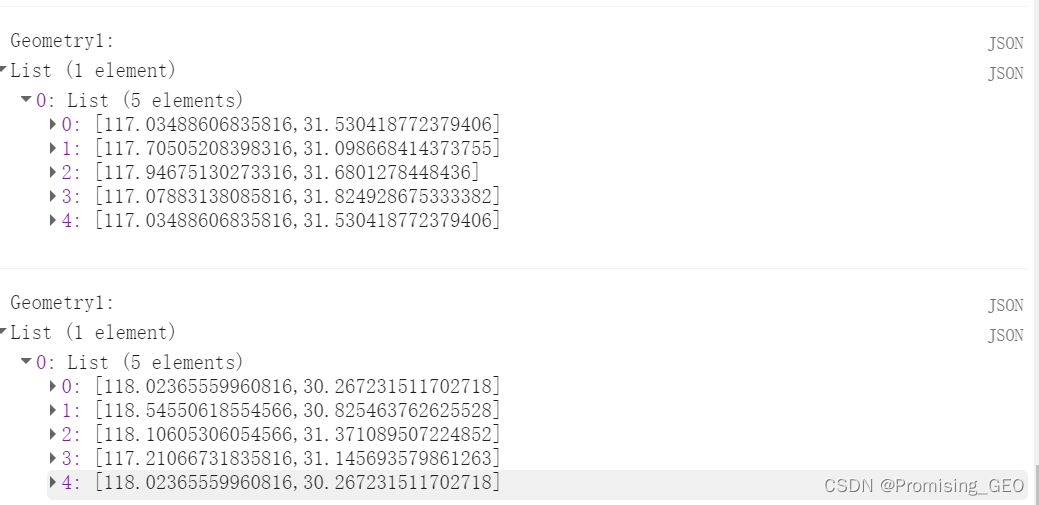
（5）判断交集和求交集

判断两个数据之间存在交集我们在前面的数据类型也讲过相似的方法，大家需要注意的就是intersects是判断时使用，结果将返回true或false，而intersection指的是求两者之间的交集。

代码如下：

//判断相交与矢量求交集
print("Is Intersects:",feature3.intersects(feature4));
var intersection = feature3.intersection(feature4);
print("Intersection:",intersection);
Map.addLayer(intersection,{"color":"yellow"},"intersection");
//

结果如下：

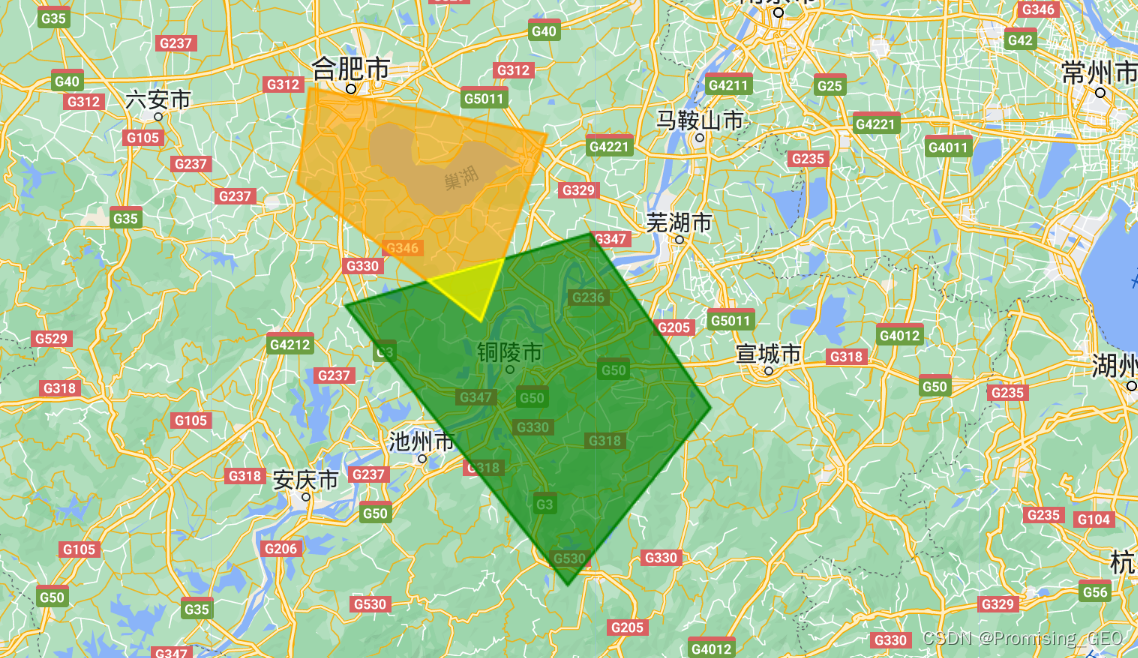
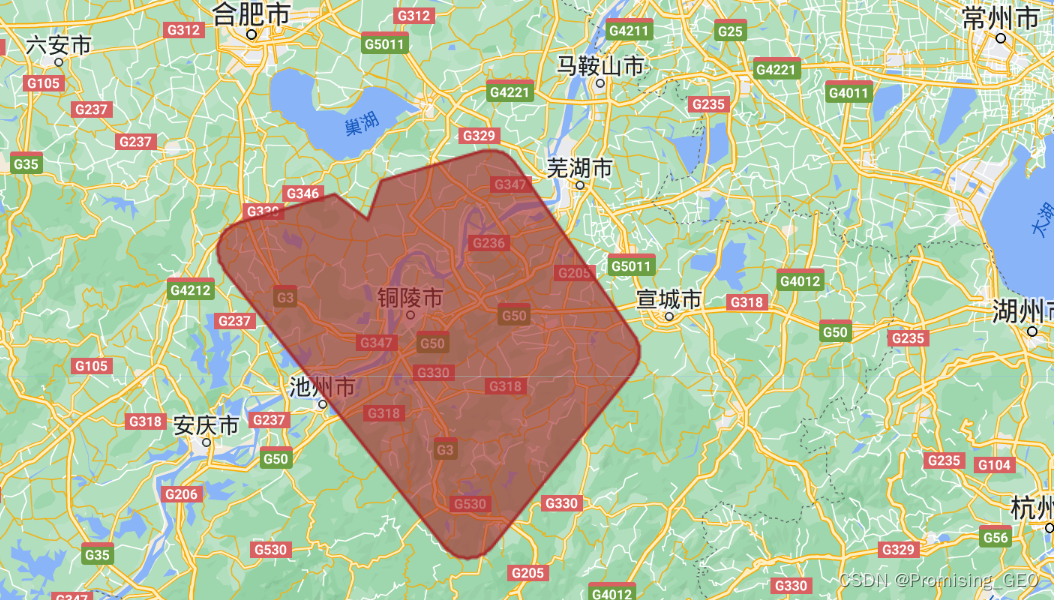
（6）缓冲区分析

缓冲区分析常常用来分析地物的影响范围，有内缓冲和外缓冲之分，以下是代码：

//缓冲区分析
//外缓冲区分析
var buffer1 = feature4.buffer(10000);
Map.addLayer(buffer1,{"color":"blue"},"buffer1");
//内缓冲区分析
var buffer2 = feature4.buffer(-10000);
Map.addLayer(buffer2,{"color":"blue"},"buffer2");
//缓冲区裁剪
var differ = buffer1.difference(buffer2);
Map.addLayer(differ,{"color":"brown"},"differ");

内外缓冲和裁剪结果如下：

好啦，以上是小编对于feature数据的全部分享，希望能够帮到大家。feature数据是了解后面featurecollection数据的窗口，希望大家对于本次分享涉及到的操作命令能够自主多学学，熟记于心。如果分享的内容对你有帮助，不要忘记给小编点赞哦！！

谢谢大家，咱们下期再会。