---------------🎈🎈题目链接🎈🎈-------------------

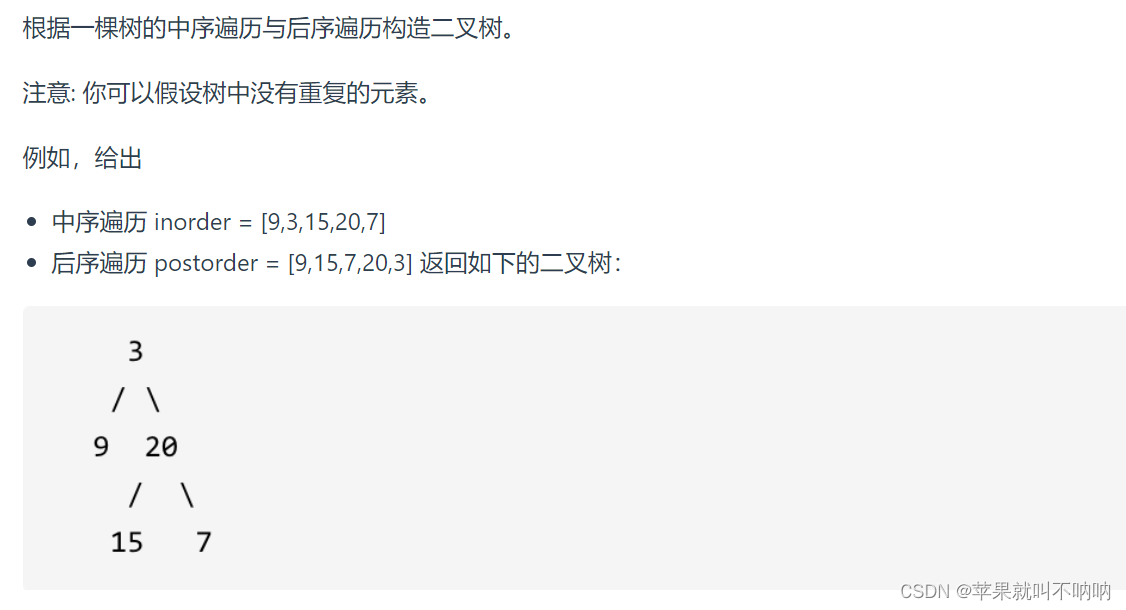
106.从中序与后序遍历序列构造二叉树

⭐️思路分析

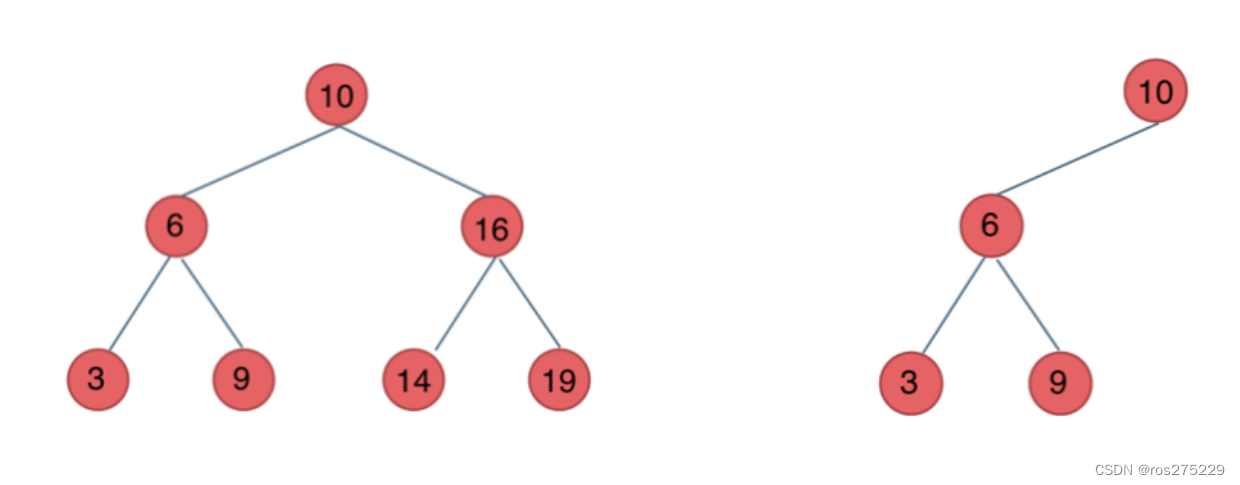
后序数组： 左 右 中
中序数组： 左 中 右
以后序数组的最后一个元素（即为根节点）为切割点，先切中序数组，
再根据中序数组的左长度，反过来再切后序数组的左和右。
一层一层切下去，每次后序数组最后一个元素就是节点元素。

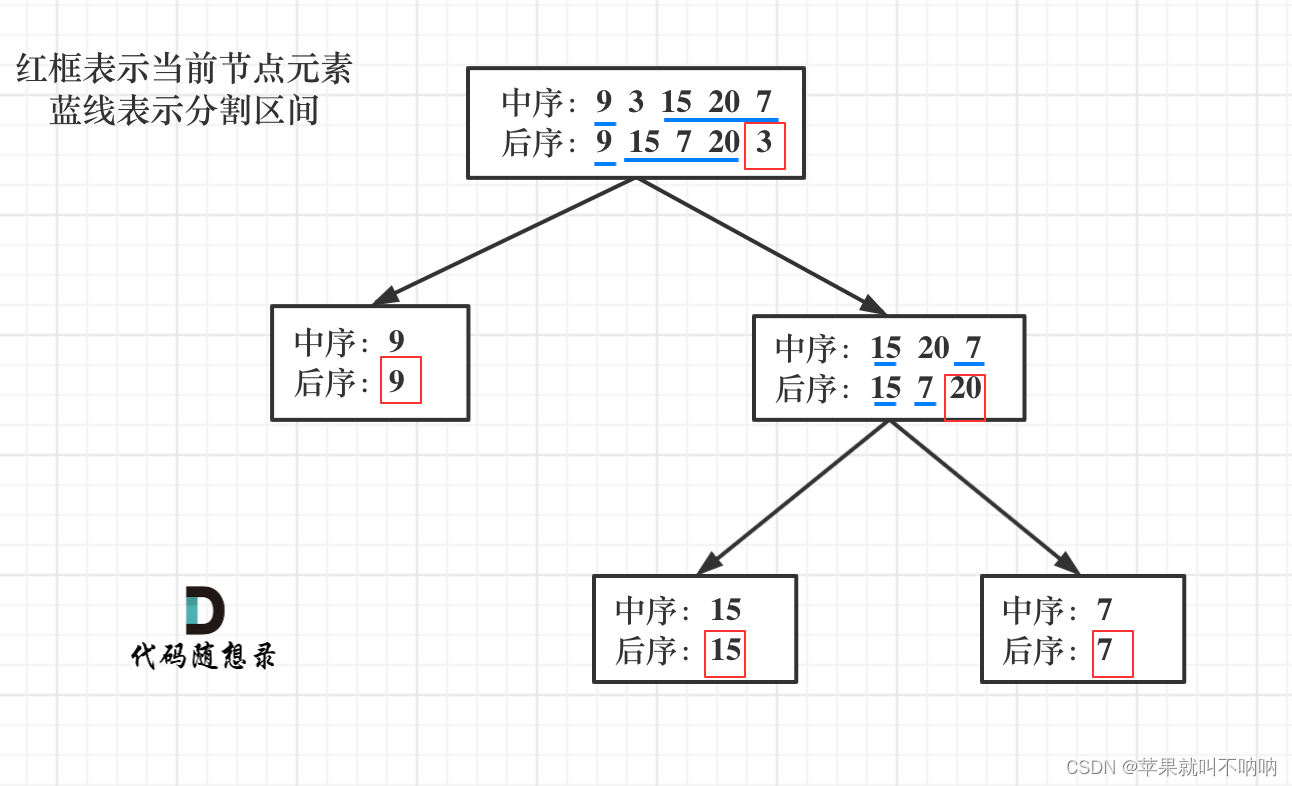
递归解法

⭐️⭐️⭐️⭐️⭐️⭐️
1. 如果数组大小为0，说明是空节点，return null
2. 如果不为空，那么取后序数组的最后一个节点
3. 找到后序数组最后一个节点 在中序数组中的位置 作为切割点
4. 切割中序数组，切成中序左数组 和 中序右数组
5. 根据中序左数组的长度，切割后序数组，切成后序左数组和后序右数组
6. 递归处理左区间和右区间

时间复杂度O(N)
空间复杂度O(N)
采用了【左闭右闭】——只要一直保持一致就行

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        //1.如果数组为空 那么就返回null
        if(inorder.length ==0 || postorder.length==0){
            return null;
        }
        return helper(inorder, postorder, 0, inorder.length-1, 0,postorder.length-1);
        //

    }
    public TreeNode helper(int[] inorder, int[] postorder, int inorderBegin, int inorderEnd, int postorderBegin, int postorderEnd){
        if(postorderBegin > postorderEnd){
            return null;
        }
        // 采用左闭右闭
        //2.如果不为空， 那么就取后序数组的最后一个元素
        int rootval = postorder[postorderEnd];
        TreeNode root= new TreeNode(rootval);

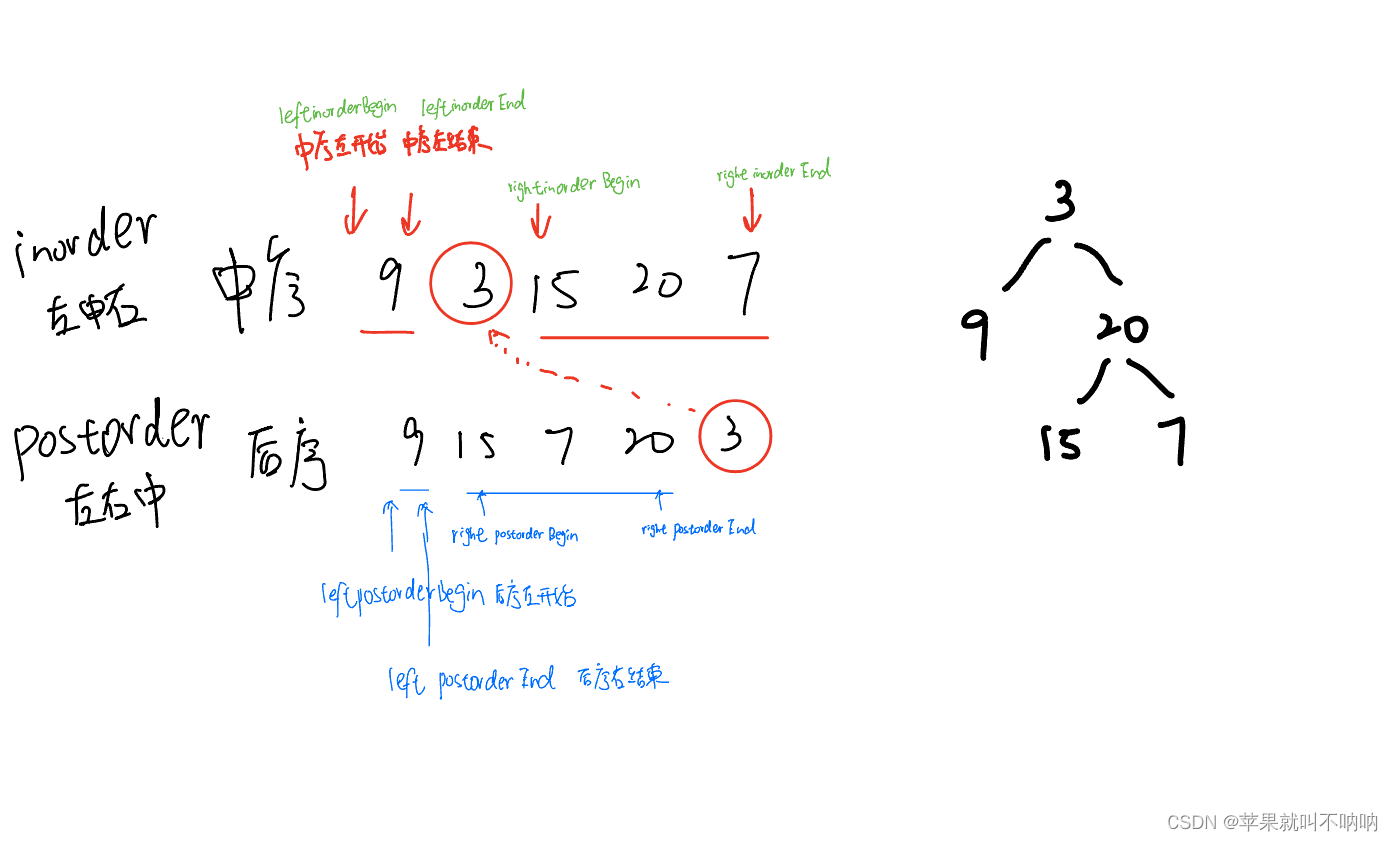
        //3.切割中序数组 得到对应中序数组中rootval所在的位置  进而得到中序左数组 中序右数组
        int midIndex;
        for(midIndex = inorderBegin; midIndex<=inorderEnd; midIndex++){
            if(inorder[midIndex] == rootval){
                break;
            }
        }
        int leftInorderBegin = inorderBegin;  // 中序左数组开头
        int leftInorderEnd = midIndex-1;      // 中序左数组结尾
        int rightInorderBegin = midIndex+1;    // 中序右数组开头
        int rightInorderEnd =  inorderEnd;     // 中序右数组结尾

        //4.根据中序左数组 切割后序数组，得到后序左数组 后序右数组
        int leftPostorderBegin = postorderBegin;                 // 后序左数组开头
        int leftPostorderEnd = postorderBegin + midIndex -inorderBegin -1;         // 后序左数组结尾
        int rightPostorderBegin = leftPostorderEnd+1;           // 后序右数组开头
        int rightPostorderEnd = postorderEnd-1;                  // 后序右数组结尾

        //5.递归处理左子树和右子树
        root.left = helper(inorder, postorder, leftInorderBegin, leftInorderEnd, leftPostorderBegin, leftPostorderEnd);
        root.right = helper(inorder, postorder, rightInorderBegin, rightInorderEnd, rightPostorderBegin, rightPostorderEnd);
        return root;
    }
}

105. 从前序与中序遍历序列构造二叉树

递归解法

⭐️⭐️⭐️⭐️⭐️⭐️
接受参数int[ ] preorder, int[ ] inorder, preorder的开始，preorder的结束，inorder的开始，inorder的结束
1. 如果数组大小为0，说明是空节点，return null
2. 从前序的第一个得到根节点root
3. 根据midval 在中序数组inorder中 寻找切割点midindex
4. 对中序数组inorder进行切割 ：中序左(begin/end) 中序右(begin/end)
5. 根据分化结果，对前序数组preorder进行切割 ：前序左(begin/end) 前序右(begin/end)
6. 进行左右子树构建递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        // 采用左闭右闭
        if(preorder.length == 0) return null;
        return helper(preorder, inorder, 0, preorder.length-1, 0, inorder.length-1);
    }
    public TreeNode helper(int[] preorder, int[] inorder, int preorderBegin, int preorderEnd, int inorderBegin, int inorderEnd){
        // 接受参数int[] preorder, int[] inorder, preorder的开始，preorder的结束，inorder的开始，inorder的结束

        // 1.如果数组大小为0，说明是空节点，return null
        if(preorderBegin > preorderEnd){
            return null;
        }

        // 2.从前序的第一个得到根节点root
        int midval = preorder[preorderBegin];
        TreeNode root = new TreeNode(midval);

        // 3. 根据midval 在中序数组inorder中 寻找切割点midindex
        int midindex;
        for(midindex = inorderBegin; midindex<=inorderEnd; midindex++){
            if(inorder[midindex] == midval){
                break;
            }
        }

        // 4.对中序数组inorder进行切割 ：中序左(begin/end) 中序右(begin/end)
        int inorderLeftBegin = inorderBegin;
        int inorderLeftEnd = midindex-1;
        int inorderRightBegin =midindex+1;
        int inorderRightEnd = inorderEnd;

        // 5.根据分化结果，对前序数组preorder进行切割 ：前序左(begin/end) 前序右(begin/end)
        int preorderLeftBegin = preorderBegin+1;
        int preorderLeftEnd = preorderLeftBegin + midindex-inorderBegin-1;
        int preorderRightBegin = preorderLeftEnd+1;
        int preorderRightEnd = preorderEnd;

        // 进行左右子树构建递归
        root.left = helper(preorder, inorder, preorderLeftBegin,preorderLeftEnd, inorderLeftBegin, inorderLeftEnd); //左
        root.right = helper(preorder, inorder, preorderRightBegin,preorderRightEnd, inorderRightBegin, inorderRightEnd); //右
        return root;

    }
}