文章目录
- 一、有监督-分类模型
- 1、混淆矩阵
- 2、分类模型的精度和召回率
- 3、ROC曲线与AUC
- 二、有监督-回归模型
- 1、均方误差MSE
- 2、 R 2 R^2 R2决定系数
- 3、回归模型代码示例
- 三、无监督模型
- 1、kmeans求解最优k值的方法:轮廓系数、肘部法
- 2、GMM的最优组件个数:AIC 和 BIC
一、有监督-分类模型
以威斯康星州乳腺癌数据集为例子
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases'
'/breast-cancer-wisconsin/wdbc.data', header=None)
df.head()

## 将数据分成标签与特征,同时对标签编码,M=1,B=0
from sklearn.preprocessing import LabelEncoder
X = df.loc[:, 2:].values
y = df.loc[:, 1].values
le = LabelEncoder()
y = le.fit_transform(y)
## 将数据拆分成训练集与测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = \
train_test_split(X, y,
test_size=0.20,
stratify=y,
random_state=1)
用scikit-learn的pipeline类,可以拟合任意多个转换步骤的模型,并将模型用于对新数据进行预测。
make_pipeline函数可以包括任意多个scikit-learn转换器,接着是实现fit及predict的scikit-learn估计器。
注意,尽管流水线的中间步骤没有数量限制,但是流水线的最后一个元素必须是估计器。
# 通过构建流水线简化流程
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
pipe_svc = make_pipeline(StandardScaler(),
SVC(random_state=1))
1、混淆矩阵
预测分类结果与实际分类结果的叉乘方阵,真正(TP)、真负(TN)、假正(FP)、假负(FP)。sklearn里提供了confusion_matrix库来快捷的计算出混淆矩阵。
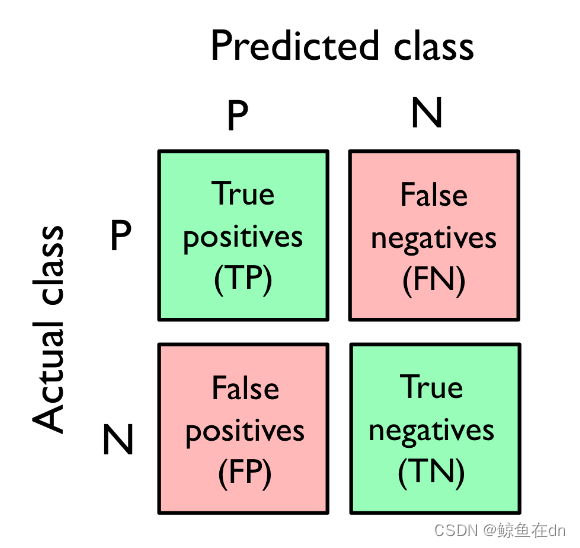
from sklearn.metrics import confusion_matrix
pipe_svc.fit(X_train, y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)

2、分类模型的精度和召回率
-
误差(error,ERR):
E R R = F P + F N F P + T P + F N + T N ERR = \frac{FP+FN}{FP+TP+FN+TN} ERR=FP+TP+FN+TNFP+FN -
准确率(accuracy,ACC):
A C C = T P + T N F P + T P + F N + T N = 1 − E R R ACC = \frac{TP+TN}{FP+TP+FN+TN} = 1-ERR ACC=FP+TP+FN+TNTP+TN=1−ERR -
真正率(TPR)和假正率(FPR),对非平衡分类问题特别有效的性能指标
F P R = F P N = F P F P + T N FPR = \frac{FP}{N} = \frac{FP}{FP+TN} FPR=NFP=FP+TNFP
T P R = T P P = T P F N + T P TPR = \frac{TP}{P} = \frac{TP}{FN+TP} TPR=PTP=FN+TPTP -
精度(PRE)和召回率(REC)
P R E = T P F P + T P PRE = \frac{TP}{FP+TP} PRE=FP+TPTP
R E C = T P R = T P F N + T P REC = TPR = \frac{TP}{FN+TP} REC=TPR=FN+TPTP -
对类别不均衡数据,常见的处理方式
- 对少数类的错误预测给予更大的惩罚
- 对少数类上采样
- 对多数类下采样
- 生成合成训练样本
from sklearn.metrics import precision_score, recall_score, f1_score
print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))
print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))
print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))

3、ROC曲线与AUC
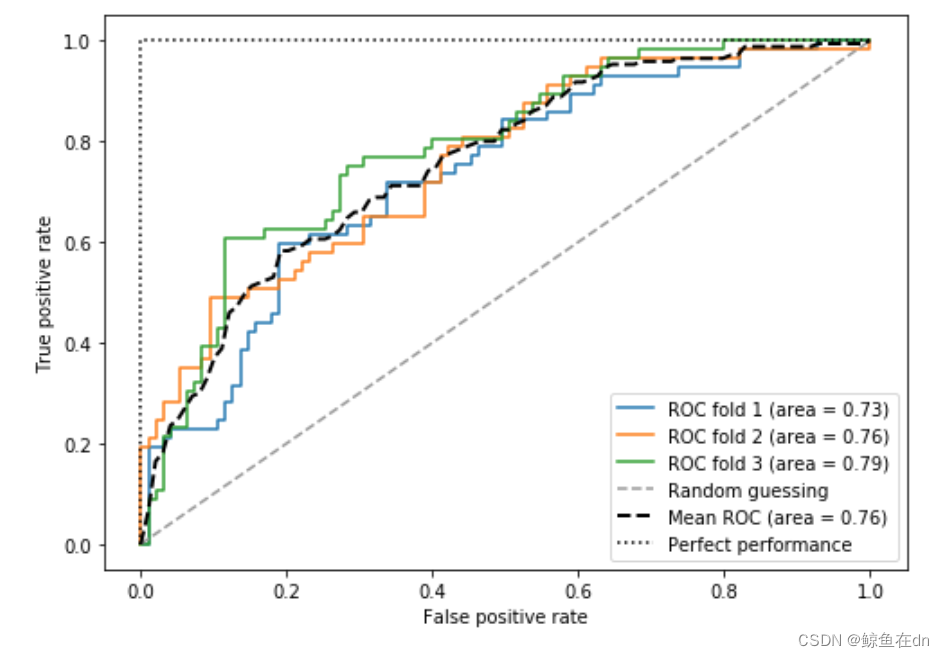
*ROC曲线(Receiver Operating Characteristic,受试者工作特征)是选择分类模型的有用工具,以FPR和TPR的性能比较结果为依据,通过移动分类器的阈值完成计算,可以计算ROC曲线下面积(AUC, Area Under the Curve)来描述分类模型的性能。如果分类器性能在对角线以下,说明性能比随机猜测还要差。tpr为1,fpr为0的完美分类器落在曲线的左上角。
from sklearn.metrics import roc_curve, auc
from distutils.version import LooseVersion as Version
from scipy import __version__ as scipy_version
import numpy as np
from sklearn.model_selection import StratifiedKFold
import matplotlib.pyplot as plt
if scipy_version >= Version('1.4.1'):
from numpy import interp
else:
from scipy import interp
pipe_lr = make_pipeline(StandardScaler(),
PCA(n_components=2),
LogisticRegression(penalty='l2',
random_state=1,
solver='lbfgs',
C=100.0))
X_train2 = X_train[:, [4, 14]]
cv = list(StratifiedKFold(n_splits=3).split(X_train, y_train))
fig = plt.figure(figsize=(7, 5))
mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []
for i, (train, test) in enumerate(cv):
probas = pipe_lr.fit(X_train2[train],
y_train[train]).predict_proba(X_train2[test])
fpr, tpr, thresholds = roc_curve(y_train[test],
probas[:, 1],
pos_label=1)
mean_tpr += interp(mean_fpr, fpr, tpr)
mean_tpr[0] = 0.0
roc_auc = auc(fpr, tpr)
plt.plot(fpr,
tpr,
label='ROC fold %d (area = %0.2f)'
% (i+1, roc_auc))
plt.plot([0, 1],
[0, 1],
linestyle='--',
color=(0.6, 0.6, 0.6),
label='Random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--',
label='Mean ROC (area = %0.2f)' % mean_auc, lw=2)
plt.plot([0, 0, 1],
[0, 1, 1],
linestyle=':',
color='black',
label='Perfect performance')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.legend(loc="lower right")
plt.tight_layout()
# plt.savefig('images/06_10.png', dpi=300)
plt.show()
二、有监督-回归模型
1、均方误差MSE
一个有用的模型性能度量是 均方误差(MSE)它仅仅是为了拟合线性回归模型二将SSE代价平均值最小化的结果。
M
S
E
=
1
n
∑
i
=
1
n
(
y
(
i
)
−
y
^
(
i
)
)
2
MSE = \frac{1}{n}\sum_{i=1}^{n}(y^{(i)} - \hat y^{(i)})^2
MSE=n1i=1∑n(y(i)−y^(i))2
SSE(error sum of squares)为残差平方和,即拟合数据和原始数据对应点的误差的平方和 S S E = ∑ i = 1 n ( y ( i ) − y ^ ( i ) ) 2 SSE = \sum_{i=1}^{n}(y^{(i)} - \hat y^{(i)})^2 SSE=∑i=1n(y(i)−y^(i))2
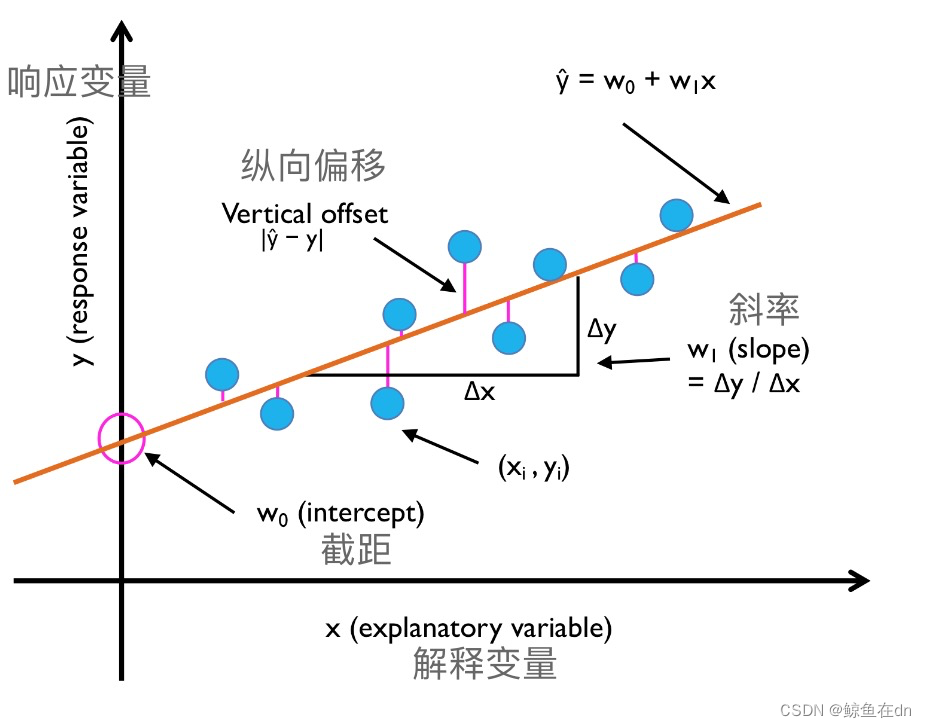
残差:线性回归可以理解为通过采样点找到最佳拟合直线,如图所示,这条最佳拟合线也被称为回归线,从回归线到样本点的垂直线就是所谓的偏移(offset)或残差(residual)——预测的误差。
2、 R 2 R^2 R2决定系数
MSE的大小取决于特征缩放,比如,如果房价用K为单位做了缩放,得出的MSE与未做缩放的原值相比更低。比如
(
10
k
−
15
k
)
2
<
(
10000
−
15000
)
2
(10k-15k)^2<(10000-15000)^2
(10k−15k)2<(10000−15000)2。这点与分类模型的准确率等指标不同。
而
R
2
R^2
R2可以理解为修正版的MSE,对于训练集,
R
2
R^2
R2的取值在0-1之间,但它也可能是负值。
R
2
R^2
R2的定义如下:
R
2
=
1
−
S
S
E
S
S
T
R^2 = 1-\frac{SSE}{SST}
R2=1−SSTSSE
SST是观测到的真实值与真实值的均值之间的差的平方和。
μ
y
μ_y
μy是真实值的均值
S
S
T
=
∑
i
=
1
n
(
y
(
i
)
−
μ
y
)
2
SST = \sum_{i=1}^{n}(y^{(i)} - μ_y)^2
SST=i=1∑n(y(i)−μy)2
3、回归模型代码示例
以波士顿住房数据集为例子
前置数据导入工作
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/'
'python-machine-learning-book-3rd-edition/'
'master/ch10/housing.data.txt',
header=None,
sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
MSE train: 19.958, test: 27.196
说明:训练数据的MSE为19.96,测试数据的MSE为27.20,测试数据的MSE比较大,这是模型过拟合训练数据的标志。
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
R^2 train: 0.765, test: 0.673
三、无监督模型
无监督模型其实已经写在了我之前的一篇文章中,反作弊中的无监督算法2_聚类的4种方式及典型算法,为了方便,我粘贴过来
1、kmeans求解最优k值的方法:轮廓系数、肘部法
参考文章:https://www.jianshu.com/p/335b376174d4
1)轮廓系数
计算集群内聚度,即样本与同一集群内所有其他点之间的平均距离
计算集群分离度,样本与最近集群内所有样本之间的平均距离
轮廓系数,计算集群内聚度 与集群分离度之差,除以两者中较大那一个。
2)肘部法:
随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。
当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数
2、GMM的最优组件个数:AIC 和 BIC
https://zhuanlan.zhihu.com/p/81255623
为了确定最优组件的个数,需要使用一些分析标准来调整模型可能性。模型中封装了Akaike information criterion (AIC) 或 Bayesian information criterion (BIC)两种评价方法。