学习资料

【MySQL数据库教程天花板，mysql安装到mysql高级，强！硬！-哔哩哔哩】
【阿里巴巴Java开发手册】https://www.w3cschool.cn/alibaba_java

事务

事务的ACID特性

原子性（atomicity）

原子性是指事务是一个不可分割的工作单位，要么全部提交，要么全部失败回滚。即要么转账成功，要么转账失败，是不存在中间状态。如果无法保证原子性会怎么样？就会出现数据不一致的情形，A账户减去100元，而B账户增加100元操作失败，系统将无故丢失100元。

一致性（consistency）

（国内很多网站上对一致性的阐述有误，具体你可以参考Wikipedia对Consistency的阐述）

根据定义，一致性是指事务执行前后，数据从一个合法性状态变换到另外一个合法性状态。这种状态是语义上的而不是语法上的，跟具体的业务有关。

那什么是合法的数据状态呢？满足预定的约束的状态就叫做合法的状态。通俗一点，这状态是由你自己来定义的（比如满足现实世界中的约束）。满足这个状态，数据就是一致的，不满足这个状态，数据就是不一致的！如果事务中的某个操作失败了，系统就会自动撤销当前正在执行的事务，返回到事务操作之前的状态。

举例1：A账户有200元，转账300元出去，此时A账户余额为-100元。你自然就发现了此时数据是不一致的，为什么呢？因为你定义了一个状态，余额这列必须>=0。

举例2：A账户200元，转账50元给B账户，A账户的钱扣了，但B账户因为各种意外，余额并没有增加，你也知道此时数据是不一致的，为什么？因为你定义了一个状态，要求A+B的总余额必须不变。

举例3：在数据表中我们将姓名字段设置为唯一性约束，这时当事务进行提交或者事务发生回滚的时候，如果数据表中的姓名不唯一，就破坏了事务的一致性要求。

隔离性（isolation）

事务的隔离性是指一个事务的执行不能被其他事务干扰，即一个事务内部的操作及使用的数据对并发的其他事务时隔离的，并发执行的各个事务直接不能互相干扰。

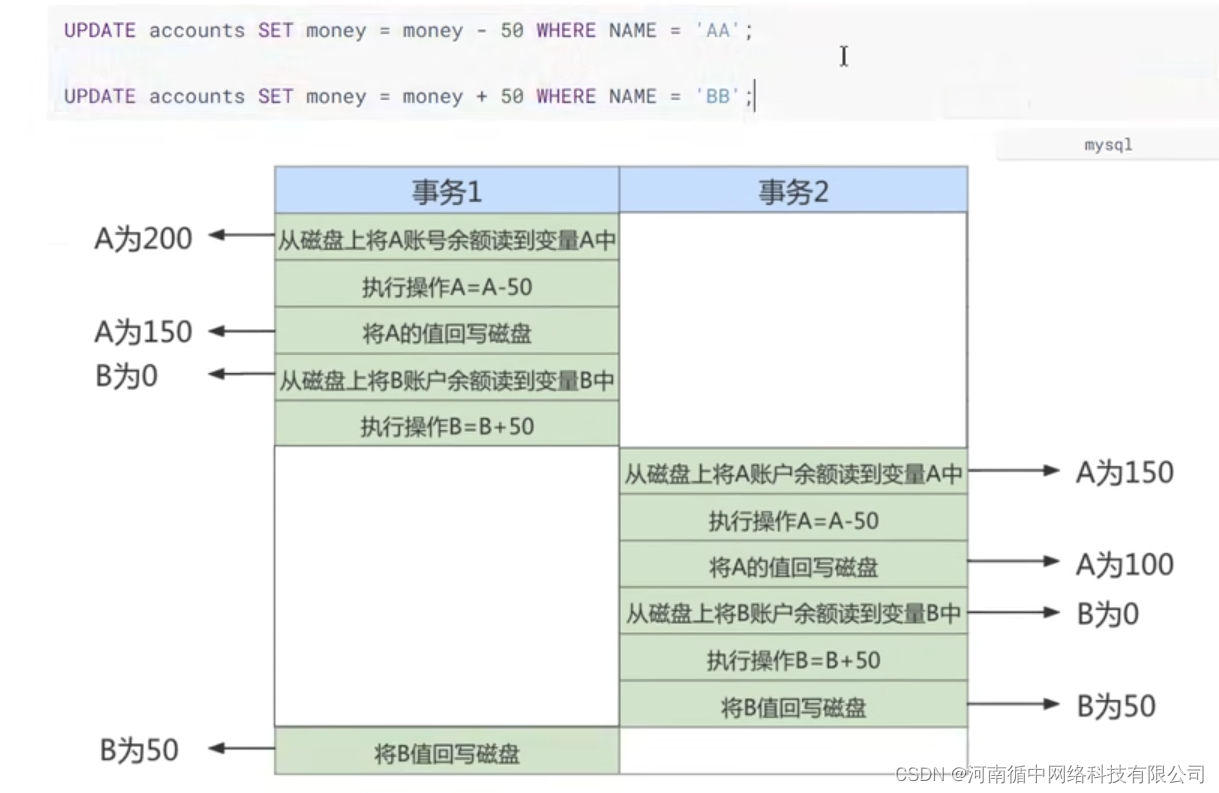
如果无法保证隔离性会怎么样？假设A账户有200元，B账户0元。A账户往B账户转账两次，每次金额为50元，分别在两个事务中执行。如果无法保证隔离性，会出现下面的情形：

持久性

持久性是指一个事务一旦被提交，它对数据库中数据的改变就是永久性的，接下来的其他操作和数据库故障不应该对其有任何影响。
持久性是通过事务日志来保证的。日志包括了重做日志和回滚日志。当我们通过事务对数据进行修改的时候，首先会将数据库的变化信息记录到重做日志中，然后在对数据库中对应的行进行修改。这样做的好处是，即时数据库系统崩溃，数据库重启后也能找到没有更新到的数据库系统中的重做日志，重新执行，从而使事务具有持久性。