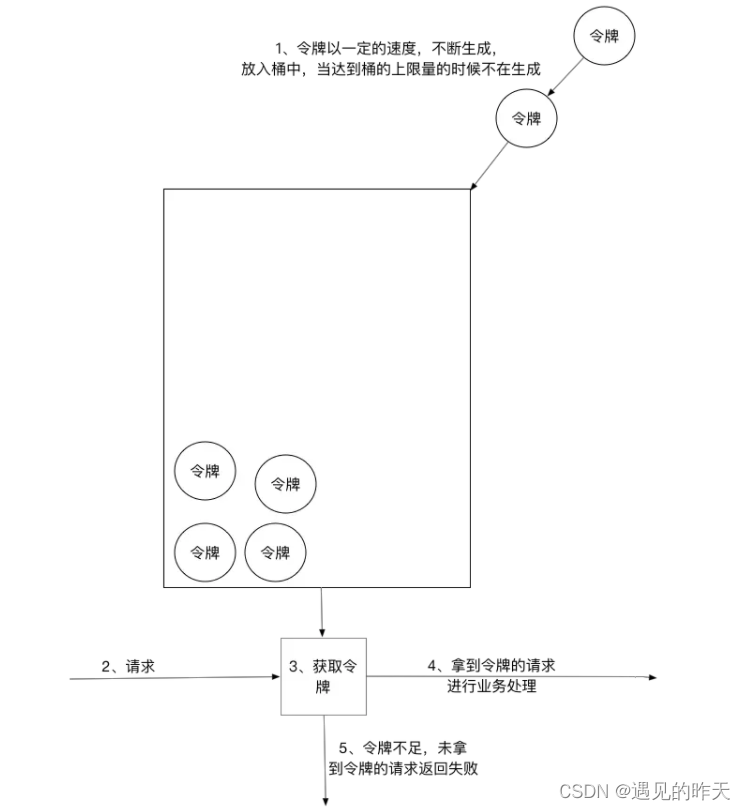
Chi square test（卡方检验）是用于评价两类变量之间是否存在相关性的统计检验方法。

医疗研究会产生大量不同类型的数据，最容易识别的是定量的数据。例如，直腿抬高 (SLR) 的受试者能够将腿抬高大于 0 度，这让我们可以计算两组的平均 SLR，并进行 t 检验。但并不是所有的数据都有这种定量特性。

例如，我们可能对两种治疗后患者的主观改善感兴趣(只使用“是”或“否”回答)，而不是测量个体的 SLR。我们能够计算每组的平均改善程度，并做 t 检验吗？答案是否。处理这类数据最为常用的分析方法是 Chi Square 相关性检验。下面是最简单的一个例子。

坐骨神经痛的患者被分成两组，分别使用推拿（SMT）和电牵引（IMT）的方法进行了治疗，治疗的分组情况和病人反馈如下：

在这个例子中，我们的观测值是分类的而非定量的，所以我们应当关注比例而非均值。

注意：$p_1+p_2=q_1+q_2=1$.

我们感兴趣的统计假设总是无事发生（0 假设）。拓展到这个例子就是，$p_1=q_1$，$p_2=q_2$；即分组 2 中个体的分布不受分组 1 的影响。

为了测试这个假设，我们需要比较假设是真的情况下，期望值和我们实际观测值的差异。

在本例中，我们有 140 个患者认为自己改善了，相对于 390 个总患者来说，改善率为 36%。所以，如果治疗和改善之间没有联系（0 假设），那么对于每一个治疗分组，都应该有 36% 的改善率。

于是有：

注：括号中为 0 假设下的期望值。

获得了期望值之后，需要比较这些值和我们实际观测值之间的差距。
${\chi }^2={\sum }_i\frac{({\mathrm{O}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}_i-{\mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}_i{)}^2}{{\mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}_i}$

计算表格如下：

此时，${\chi }^2=32.53$。

根据${\chi }^2$ 的计算公式我们知道，当零假设成立时，${\chi }^2$ 的值会比较小，反之亦然。

接下来的问题是，当 ${\chi }^2$ 多大时，我们会拒绝 0 假设？

${\chi }^2$ 值来自于 Chi Square distribution，这个分布由一个参数决定，即自由度。自由度取决于我们分析的表的大小，可用接下来的公式进行计算。

我们检测的 p-value（任何 2×2 table 的卡方检验），是计算出的卡方值到坐标最右侧曲线下的面积。

查表可知，当卡方值在 6.64 时，p-value 已经小于 0.01。由于我们的值是 32.53，其 p-value 自然小于 0.01。因此，我们拒绝了 0 假设并得出结论：患者接受两种治疗方式的受益是不一样的。

在很多实验中，改善会分多个 levels。例如，让我们对使用热包的脊椎按摩 (Trt 1) 和使用冷包的脊椎按摩 (Trt 2) 治疗急性腰痛进行比较试验。我们使用了 5 个分类来描述改善的状况：

零假设是，两种治疗方式没有差异。

下面计算零假设下的期望值以及最终的卡方值。

此时，自由度为：$(2-1)\times (5-1)=4$。

自由度为 4 的 Chi Square distribution 如下

卡方为 7.43 时，p-value 是 0.1148。如果我们的显著性水平定为 0.05，则我们无法拒绝零假设。此时，结论是两种治疗手段没有显著的区别。

要进一步解释这一点，请考虑表 8，其中的数据已转换为行百分比：

严格地讲，这些概率分布的比例并不相同。然而考虑到数据中的随机错误，我们没有足够的证据来说明观察到的差异表明了真正的潜在差异。

最后，在使用${\chi }^2$ 检验时，需要遵循一些关键假设，包括了：

每个个体在表中只出现一次；
每个个体的结果独立于其他所有个体的结果；
期望值表中应该有 80% 的期望值大于 5。

参考文献

Ugoni A, Walker BF. The Chi square test: an introduction. COMSIG Rev. 1995 Nov 1;4(3):61-4. PMID: 17989754; PMCID: PMC2050386.