二叉树的链式结构实现
- 1. 链式存储
- 2. 二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 3. 二叉树遍历的代码实现
- 前序遍历
- 中序遍历
- 后序遍历
- 4. 二叉树各种相关函数的实现
- 二叉树节点个数
- 二叉树叶子节点个数
- 二叉树的高度
- 二叉树第k层节点个数
- 二叉树查找值为x的节点
- 5. 代码验证
1. 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
typedef int BTDataType;
// 二叉链
typedef struct BinaryTreeNode
{
BTDataType data;// 当前节点值域
struct BinaryTreeNode* left;// 指向当前节点左孩子
struct BinaryTreeNode* right;// 指向当前节点右孩子
}BTNode;
2. 二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
前序遍历
前序遍历:访问根结点的操作发生在遍历其左右子树之前
根 - > 左子树 - > 右子树
前序遍历:
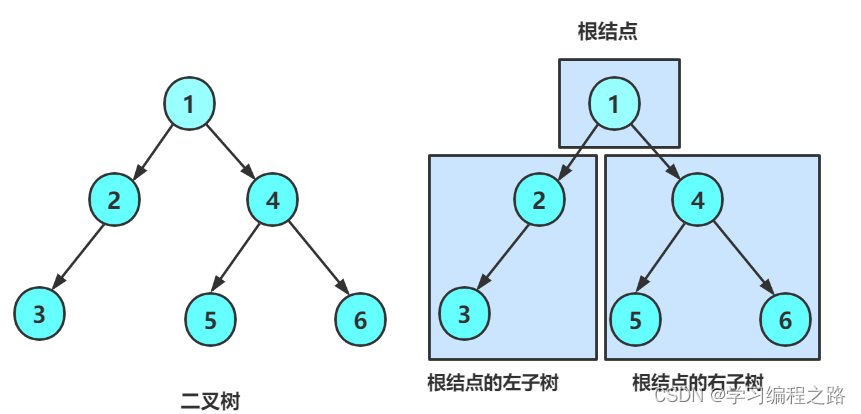
遍历顺序:1 -> 2 -> 3 -> NULL -> NULL -> NULL -> 4 -> 5 -> NULL - >NULL6 -> NULL - >NULL 。
中序遍历
中序遍历:访问根结点的操作发生在遍历其左右子树之中。
左子树 - > 根 - > 右子树
中序遍历:

遍历顺序:NULL -> 3 -> NULL -> 2 -> NULL -> 1 - > NULL - > 5 - > NULL -> 4 - > NULL -> 6 -> NULL
后序遍历
后序遍历:访问根结点的操作发生在遍历其左右子树之后。
左子树 - > 右子树 - > 根
后序遍历:

遍历顺序:NULL -> NULL -> 3 ->NULL -> 2 - > NULL -> NULL -> 5 - > NULL -> NULL -> 6 -> 4 -> 1。
3. 二叉树遍历的代码实现
首先,要实现二叉树的遍历,我们先手动创建一棵二叉树。
和链表类似,为了方便,我们定义一个申请节点的函数。
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
创建如图所示的二叉树,只需要把左右指针连接好就可以了。
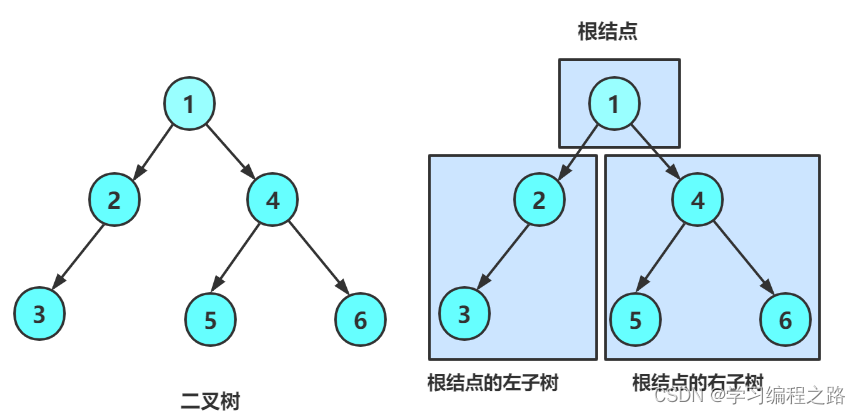
BTNode* CreatBinary()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
前序遍历
#include <stdio.h>
#include <stdlib.h>
// 二叉树前序遍历
void PrevOrder(BTNode*root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
int main()
{
BTNode* boot = CreatBinary();
PrevOrder(boot);
return 0;
}
前序遍历递归图解:
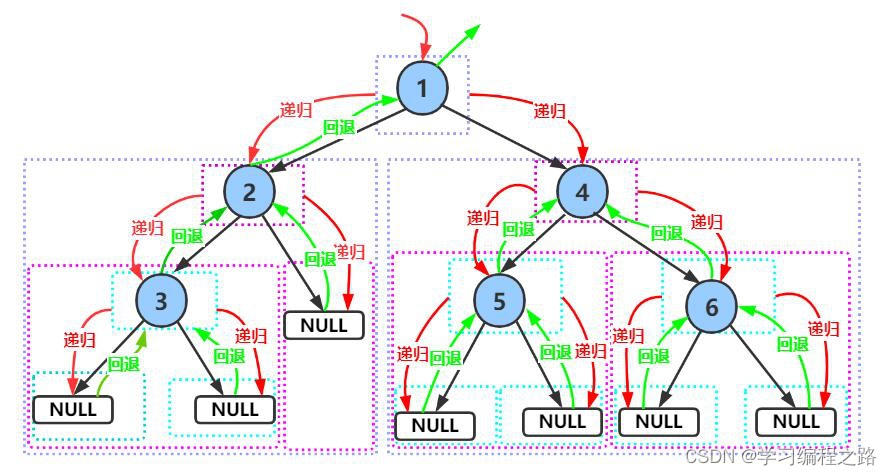
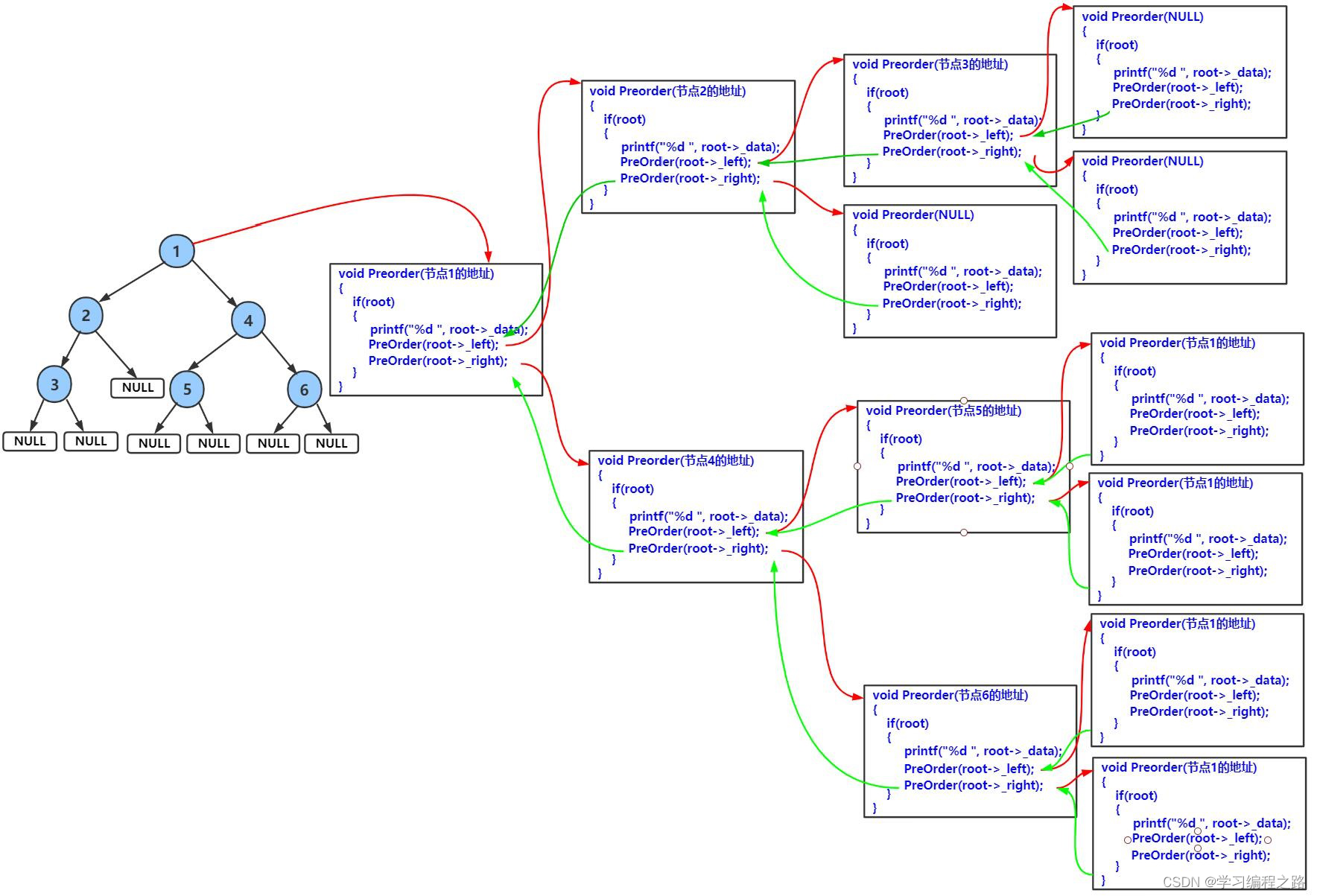
运行结果如图:
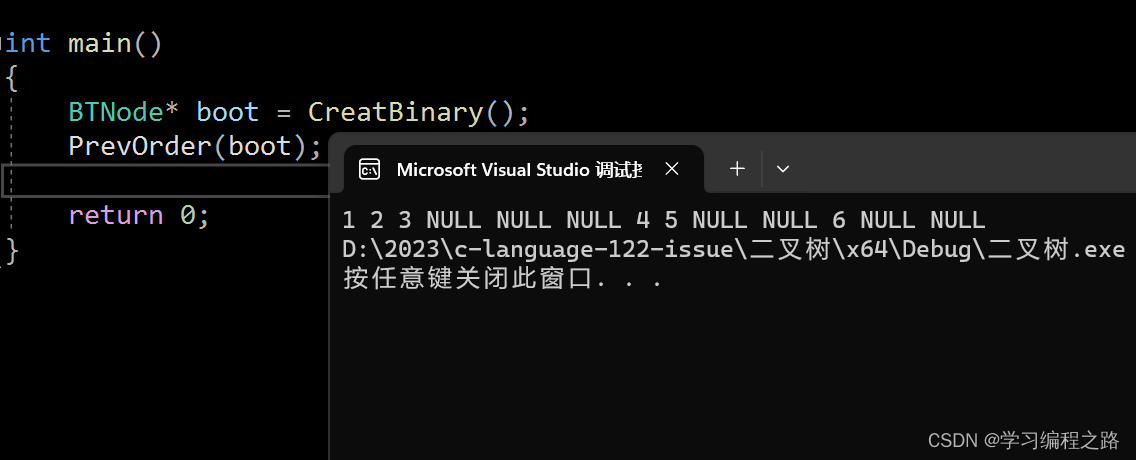
中序遍历
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
运行结果如图:
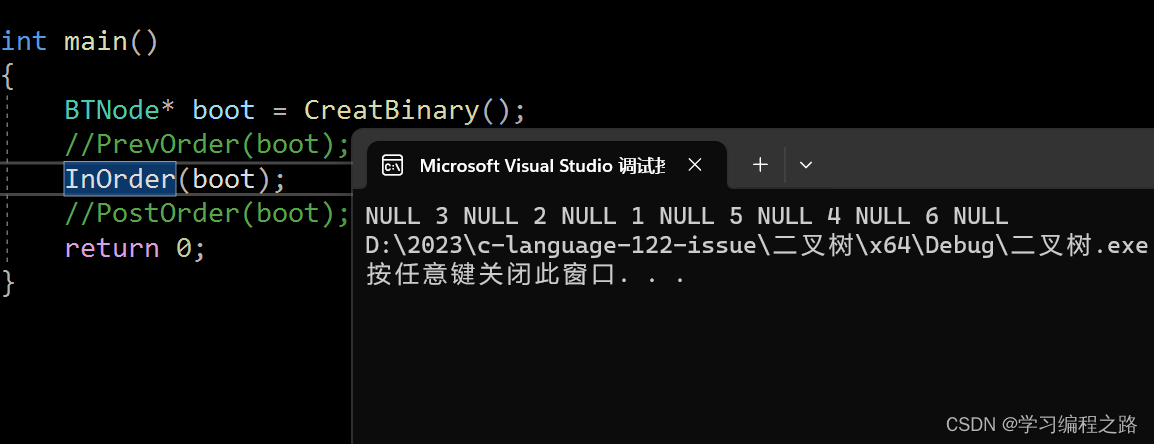
后序遍历
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
运行结果如图:
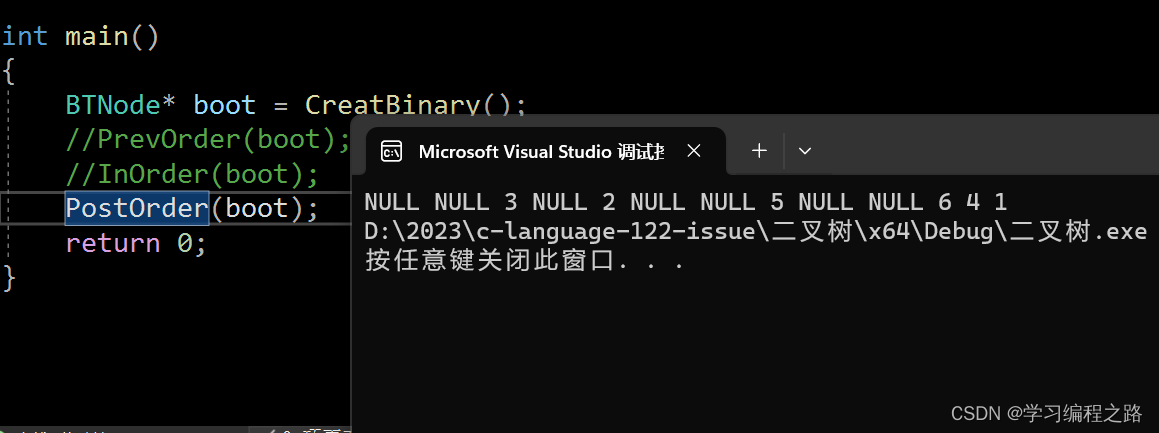
4. 二叉树各种相关函数的实现
二叉树节点个数
方法一:
求二叉树的节点个数,我们可以遍历所有节点,如果该节点不是空就计数加一,最终就可以得到二叉树节点的个数,但是注意,尽量不要在递归函数内定义变量,因为函数在递归调用的时候,开辟的空间都是独立的,我们在函数内部定义的局部变量会重复定义,所以,我们最好定义一个全局变量,这样函数递归调用的时候使用的就是同一个变量。
int size = 0;
int BTreeSize(BTNode* root)
{
if (root == NULL)
{
return size;
}
size++;
BTreeSize(root->left);
BTreeSize(root->right);
}
方法二:
求二叉树节点的个数,可以转换为:
- 如果节点为空,则没有节点返回0
- 如果节点不为空,节点的个数 = 左子树的个数 + 右子树的个数 + 自己(1)
int BTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
二叉树叶子节点个数
- 如果节点为,则叶子节点的个数为0,返回0
- 如果节点的左右指针都为空,则叶子节点的个数为1,返回1
- 如果不是叶子节点,也不是空节点,叶子节点的个数 = 左子树叶子节点的个数 + 右子树叶子节点的个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
二叉树的高度
- 如果节点为空,则高度为0,返回0
- 如果节点不为空,则树的高度 = 左右子树中的较大高度的子树 + 1
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int left = BinaryTreeHeight(root->left);
int right = BinaryTreeHeight(root->right);
if (left > right)
{
return left + 1;
}
else
{
return right + 1;
}
}
二叉树第k层节点个数
- 如果节点为空,则返回0
- 如果节点不为空,k == 1,则第k层节点个数为1,返回1
- 如果节点不为空,二叉树第k层节点个数 = 左子树的的第k - 1层 + 右子树的的第k - 1层
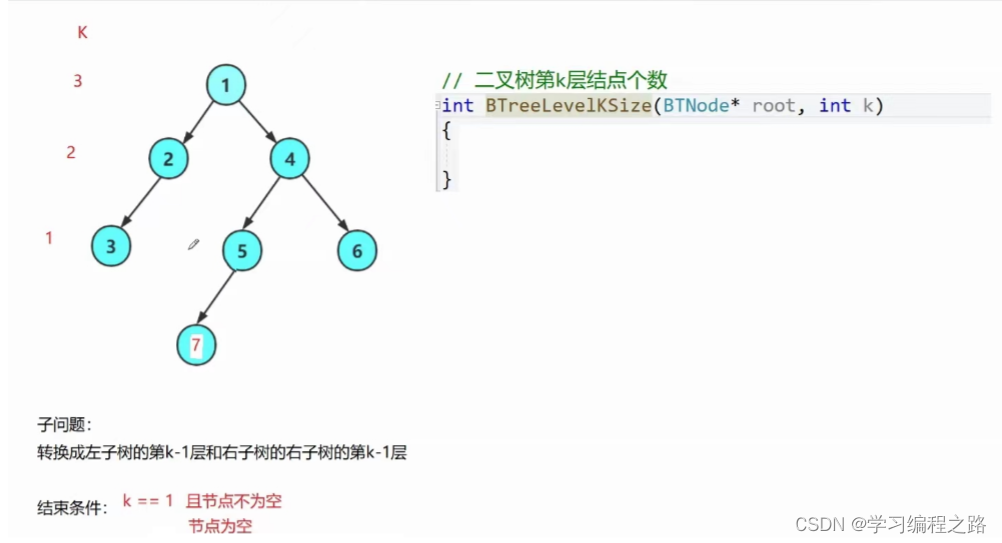
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
- 如果节点为空,则找不到返回NULL
- 如果节点不为空,先看根的值是否是x,如果不是,则查找左子树和右子树是否存在节点的值为x
- 如果左子树找到返回左子树找到的节点,如果右子树找到返回右子树找到的节点,如果左子树和右子树都找不到,则返回NULL
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2)
{
return ret2;
}
return NULL;
}
5. 代码验证
验证树的节点如图:
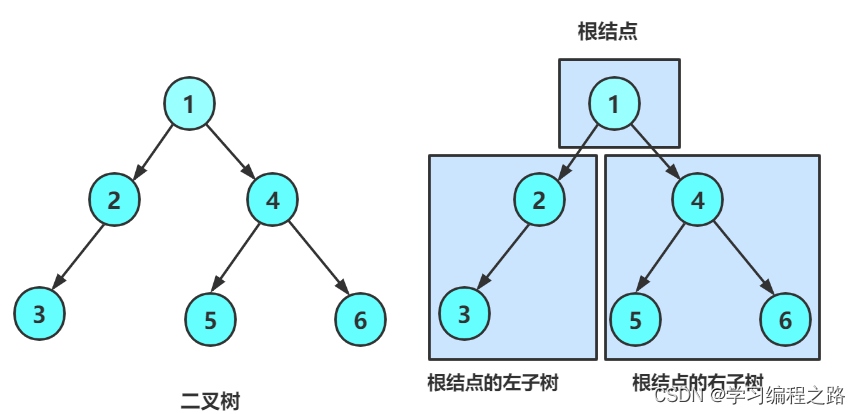
验证代码如下:
int main()
{
BTNode* root = CreatBinary();
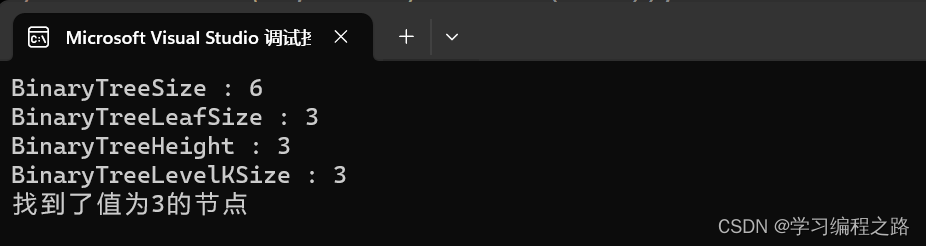
printf("BinaryTreeSize : %d\n", BinaryTreeSize(root));
printf("BinaryTreeLeafSize : %d\n", BinaryTreeLeafSize(root));
printf("BinaryTreeHeight : %d\n", BinaryTreeHeight(root));
printf("BinaryTreeLevelKSize : %d\n", BinaryTreeLevelKSize(root,3));
BTNode* ret = BinaryTreeFind(root, 3);
if (ret == NULL)
{
printf("找不到\n");
}
else
{
printf("找到了值为%d的节点\n", ret->data);
}
return 0;
}
运行结果如图: