在C++23的协程特性里, co_yield 用于从协程执行过程中返回值。这个功能乍一听起来很奇怪,网上的例子大多是用一个计数器来演示多次中断协程函数,返回顺序的计数值。这看起来毫无意义。
其实这个功能主要想演示的就是协程 co_yield 具备打断一个函数的执行,并多次返回值的能力。这种能力允许实现一种隐式状态机,每次使用时,返回下一个状态。这对于极为复杂的状态计算来说,是很有用的。它(协程)避免了显式的设置状态记忆句柄,大大简化了实现难度。同时,由于可以任意打断执行,便于在中间获取、展示一些数据状态、甚至单步调试,对构造一些教学程序意义重大。典型的是观察堆排序的中间态,不需要大幅度修改排序算法插入很多的printf,而是在函数外部做。
我们以产生任意P(N,M)、C(N,M)这样的排列、组合数序列为例子,看看传统算法和协程的区别。
1. 回溯法迭代排列组合
传统的回溯法,求取一个排列的算法如下:
void pnm_calc(const int n, const int m)
{
std::vector<int> vec_buf,vec_bz;
int swim = 0;
bool finished = false;
for (int i=0;i<m;++i) vec_buf.push_back(0);
for (int i=0;i<n;++i) vec_bz.push_back(0);
do
{
int ch = 0;
if (swim<m)
{
while (vec_bz[ch])
++ch;
vec_buf[swim] = ch;
vec_bz[ch] = 1;
++swim;
}
if (swim==m)
{
//打印
for (int i=0;i<m;++i)
printf("%d,",vec_buf[i]);
printf("\n");
bool hit = false;
do
{
if (swim<m && swim >=0) vec_bz[vec_buf[swim]] = 0;
--swim;
if (swim>=0)
{
int nextv = vec_buf[swim];
do
{
++nextv;
if (nextv >=n)
break;
if (vec_bz[nextv]==0)
hit = true;
} while (hit == false);
if (hit==true)
{
vec_bz[vec_buf[swim]] = 0;
vec_buf[swim] = nextv;
vec_bz[nextv] = 1;
++swim;
}
}
else
finished = true;
} while (finished == false && hit == false);
}
}while(finished == false);
};
int main(int argc, char *argv[])
{
pnm_calc(4,3);
return 0;
}
输出:
0,1,2,
0,1,3,
0,2,1,
0,2,3,
...
3,1,2,
3,2,0,
3,2,1,
2 传统状态机封装
上述打印显示结果演示的是回溯法本身。若为了更好地使用组合数,需要对算法进行封装,以便于批量的获取、运用组合数的各组结果。比如考虑到总数可能很大,需要分批次返回结果等功能,显著增加了工作量。
#include <vector>
#include <cstdio>
struct tag_NM_State
{
std::vector<unsigned short> vec_buf;
std::vector<unsigned short> vec_bz;
int swim;
bool finished;
};
/*!
\brief pnm 快速算法,使用带有记忆效应的 tag_NM_State 记录穷尽进度很好的避免了重新计算的耗时
\fn pnm
\param n N,集合数
\param m M, 子集
\param vec_output 存储结果的集合,本集合会自动增长
\param state 状态存储
\param limit 本次最多样本数
\return int 本次给出的样本数
*/
int pnm(int n, int m, std::vector<std::vector <unsigned short> > & vec_output,tag_NM_State * state, int limit/* = 0*/)
{
std::vector<unsigned short> & vec_buf = state->vec_buf,
& vec_bz = state->vec_bz;
int &swim = state->swim;
bool &finished = state->finished;
const bool firstRun = vec_output.size()?false:true;
if (vec_bz.size()==0)
{
for (int i=0;i<m;++i) vec_buf.push_back(0);
for (int i=0;i<n;++i) vec_bz.push_back(0);
swim = 0;
finished = false;
}
if (finished==true)
return 0;
int group = 0;
do
{
int ch = 0;
if (swim<m)
{
while (vec_bz[ch])
++ch;
vec_buf[swim] = ch;
vec_bz[ch] = 1;
++swim;
}
if (swim==m)
{
if (!firstRun)
memcpy(vec_output[group].data(),vec_buf.data(),m*sizeof(unsigned short));
else
vec_output.push_back(vec_buf);
++group;
bool hit = false;
do
{
if (swim<m && swim >=0) vec_bz[vec_buf[swim]] = 0;
--swim;
if (swim>=0)
{
int nextv = vec_buf[swim];
do
{
++nextv;
if (nextv >=n)
break;
if (vec_bz[nextv]==0)
hit = true;
} while (hit == false);
if (hit==true)
{
vec_bz[vec_buf[swim]] = 0;
vec_buf[swim] = nextv;
vec_bz[nextv] = 1;
++swim;
}
}
else
finished = true;
} while (finished == false && hit == false);
if (group>=limit && limit>0)
break;
}
}while(finished == false);
return group;
}
int main(int argc, char *argv[])
{
QCoreApplication a(argc, argv);
using std::vector;
tag_NM_State state;
const int n = 4, m = 3, group = 10;
vector<vector<unsigned short> > result;
int ret = pnm(n,m,result,&state,group);
while (ret>0)
{
printf("\ngroup contains %d results:\n",ret);
for (int i=0;i<ret;++i)
{
printf("\n\t");
for (int j=0;j<m;++j)
printf("%d ",result[i][j]);
}
ret = pnm(n,m,result,&state,group);
}
printf("\nFinished\n");
return 0;
}
分批输出:
group contains 10 results:
0 1 2
0 1 3
0 2 1
0 2 3
0 3 1
0 3 2
1 0 2
1 0 3
1 2 0
1 2 3
group contains 10 results:
1 3 0
1 3 2
2 0 1
2 0 3
2 1 0
2 1 3
2 3 0
2 3 1
3 0 1
3 0 2
group contains 4 results:
3 1 0
3 1 2
3 2 0
3 2 1
Finished
详细算法参考 https://goldenhawking.blog.csdn.net/article/details/80037669
3. 协程封装
使用C++23 协程后,使用变得非常简洁:
int main(int argc, char *argv[])
{
const int n = 4 , m = 3;
nmCalc pnm = pnm_calc(n,m);
while (pnm.next())
{
const int * res = pnm.currResult();
printf("\n\t");
for (int j=0;j<m;++j)
printf("%d ",res[j]);
}
}
每次调用 pnm.next() 就返回下一组结果且无需记忆状态。
但这也是有代价的!为了达到上述的效果,协程封装如下:
#ifndef NMCALC_H
#define NMCALC_H
#include<coroutine>
#include<vector>
class nmCalc
{
public:
struct promise_type {
//记录本次排列组合的结果
const int * m_currResult;
auto get_return_object() { return nmCalc{ handle::from_promise(*this) }; }
auto initial_suspend() { return std::suspend_always{}; }
auto final_suspend() noexcept { return std::suspend_always{}; }
void unhandled_exception() { return ;}
void return_void(){}
auto yield_value(const int * result ) {this->m_currResult=result; return std::suspend_always{}; }
};
using handle = std::coroutine_handle<promise_type>;
private:
handle hCoroutine;
nmCalc(handle handle) :hCoroutine(handle) {}
public:
nmCalc(nmCalc&& other)noexcept :hCoroutine(other.hCoroutine) { other.hCoroutine = nullptr; }
~nmCalc() { if (hCoroutine) hCoroutine.destroy(); }
//请求下一组结果,调用后 co_yield继续。
bool next() const { return hCoroutine && (hCoroutine.resume(), !hCoroutine.done()); }
const int * currResult() const { return hCoroutine.promise().m_currResult; }
};
nmCalc pnm_calc(const int n, const int m)
{
std::vector<int> vec_buf,vec_bz;
int swim = 0;
bool finished = false;
for (int i=0;i<m;++i) vec_buf.push_back(0);
for (int i=0;i<n;++i) vec_bz.push_back(0);
do
{
int ch = 0;
if (swim<m)
{
while (vec_bz[ch])
++ch;
vec_buf[swim] = ch;
vec_bz[ch] = 1;
++swim;
}
if (swim==m)
{
//返回一组结果!!!!!
co_yield vec_buf.data();
bool hit = false;
do
{
if (swim<m && swim >=0) vec_bz[vec_buf[swim]] = 0;
--swim;
if (swim>=0)
{
int nextv = vec_buf[swim];
do
{
++nextv;
if (nextv >=n)
break;
if (vec_bz[nextv]==0)
hit = true;
} while (hit == false);
if (hit==true)
{
vec_bz[vec_buf[swim]] = 0;
vec_buf[swim] = nextv;
vec_bz[nextv] = 1;
++swim;
}
}
else
finished = true;
} while (finished == false && hit == false);
}
}while(finished == false);
};
4. 体会与思考
这种封装方式,显著提高了算法流程的紧凑程度。无需考虑如何巧妙的保留状态,而是直接借助协程随时打断并返回。
这在算法极其复杂的情况下,尤其有效。同时,对于单步演示,比如按一下按钮出一次,也很方便,主要代码参考:
https://gitcode.net/coloreaglestdio/qtcpp_demo/-/tree/master/qt_coro_test
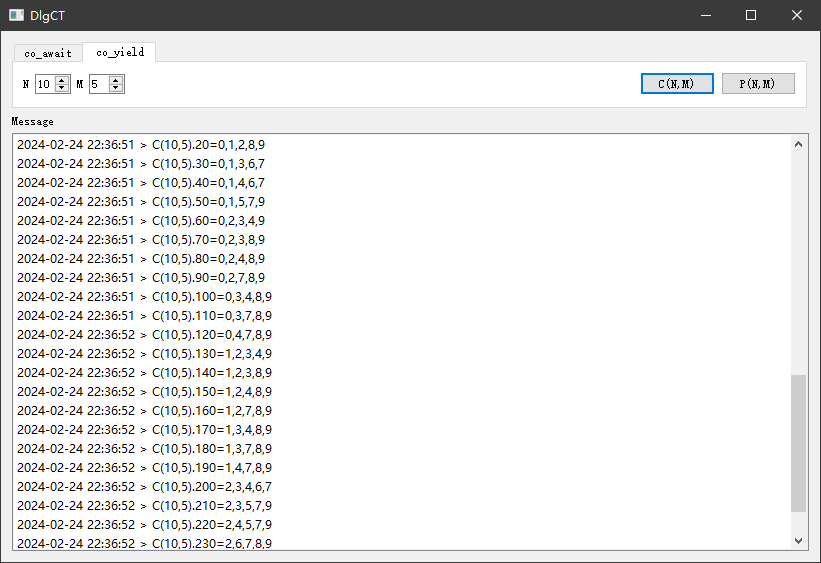
运行效果: