文章目录
- 背包问题
- 背包题目
- 解法一 ● 01背包问题-二维数组
- 五部曲
- 1.确定dp数组
- 2、确定递推公式
- 3、初始化dp数组
- 4、循环
- 代码:
- 解法二-01背包问题-滚动数组
- 五部曲1:定义dp
- 二、递推公式
- 三、初始化
- 四、循环顺序
- 代码:
- 698. 划分为k个相等的子集
- 题解:
- 代码:
- ● 416. 分割等和子集
- 思路:-自己没思路
- 动归五部曲-1.确定dp数组以及下标的含义
- 2.递推公式
- 3. dp数组如何初始化
- 4.确定遍历顺序
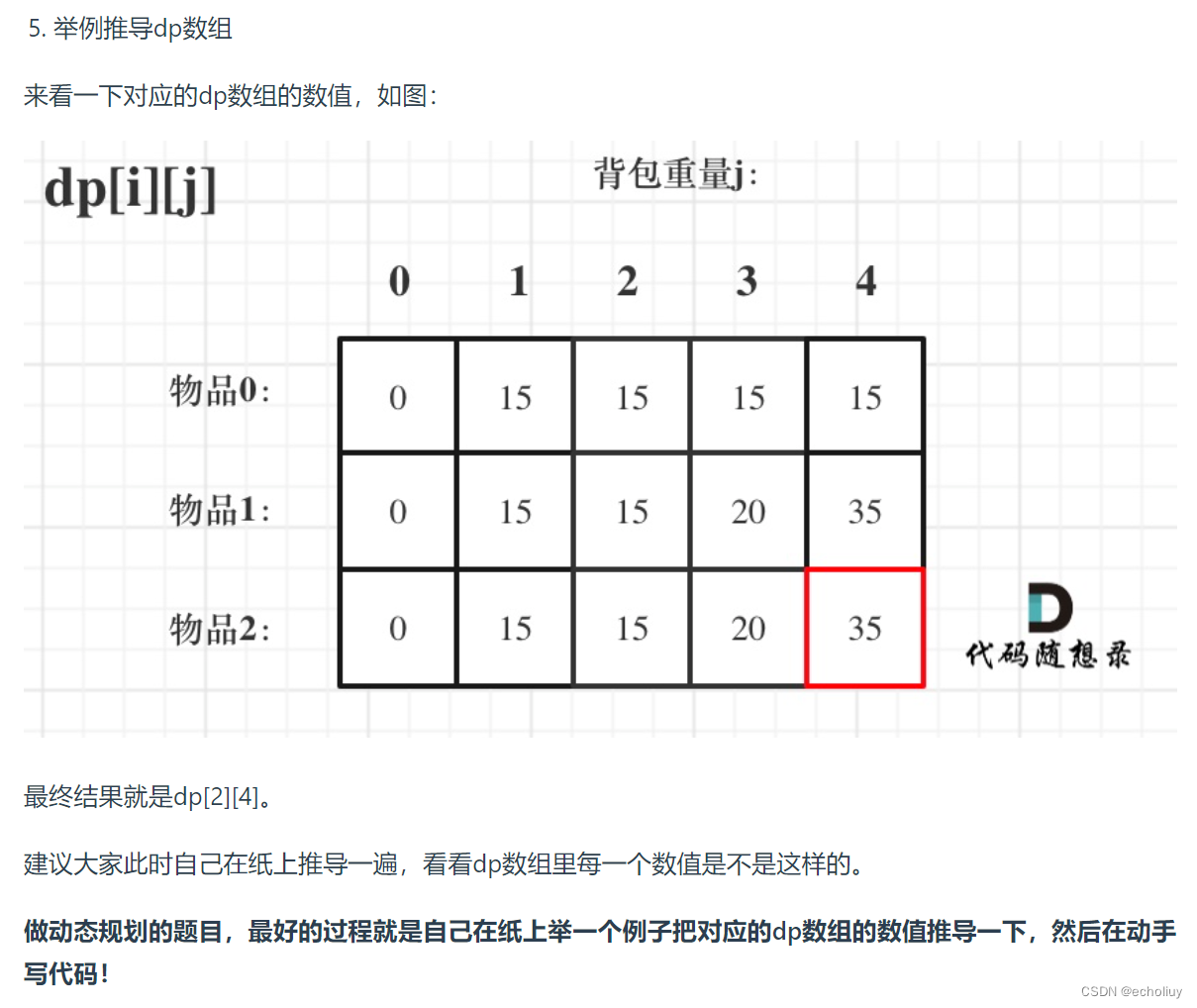
- 5. dp数组
- 代码:
背包问题
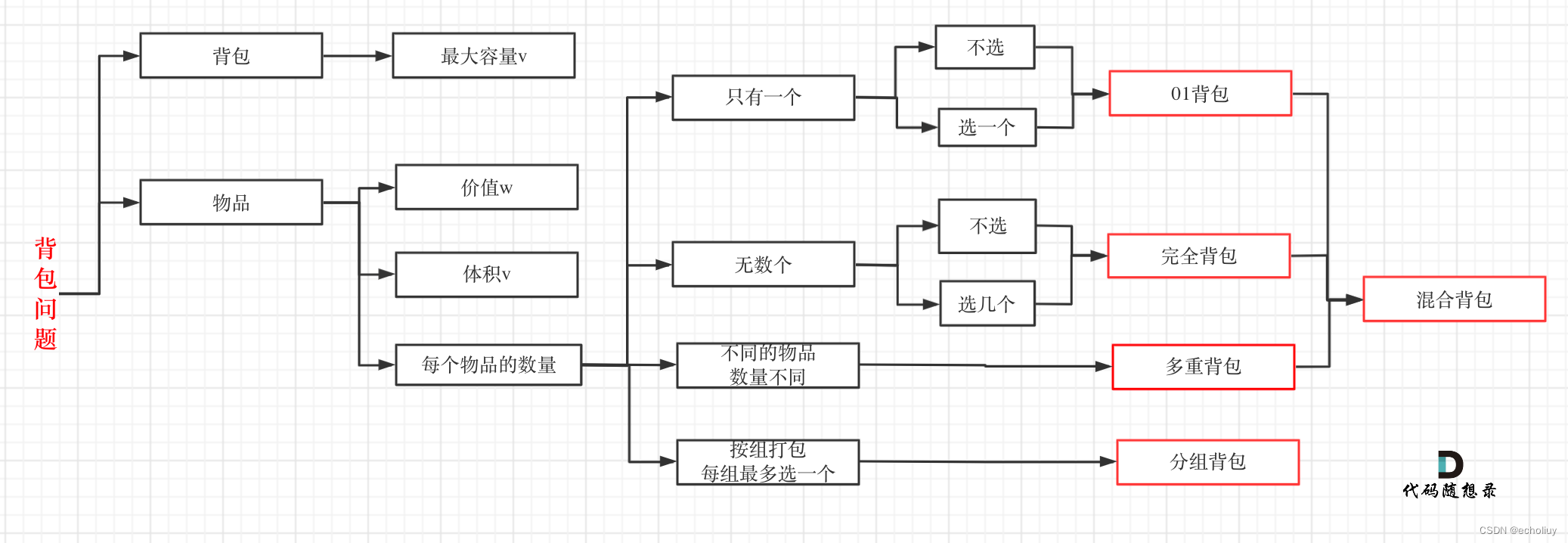
背包题目

解法一 ● 01背包问题-二维数组
五部曲
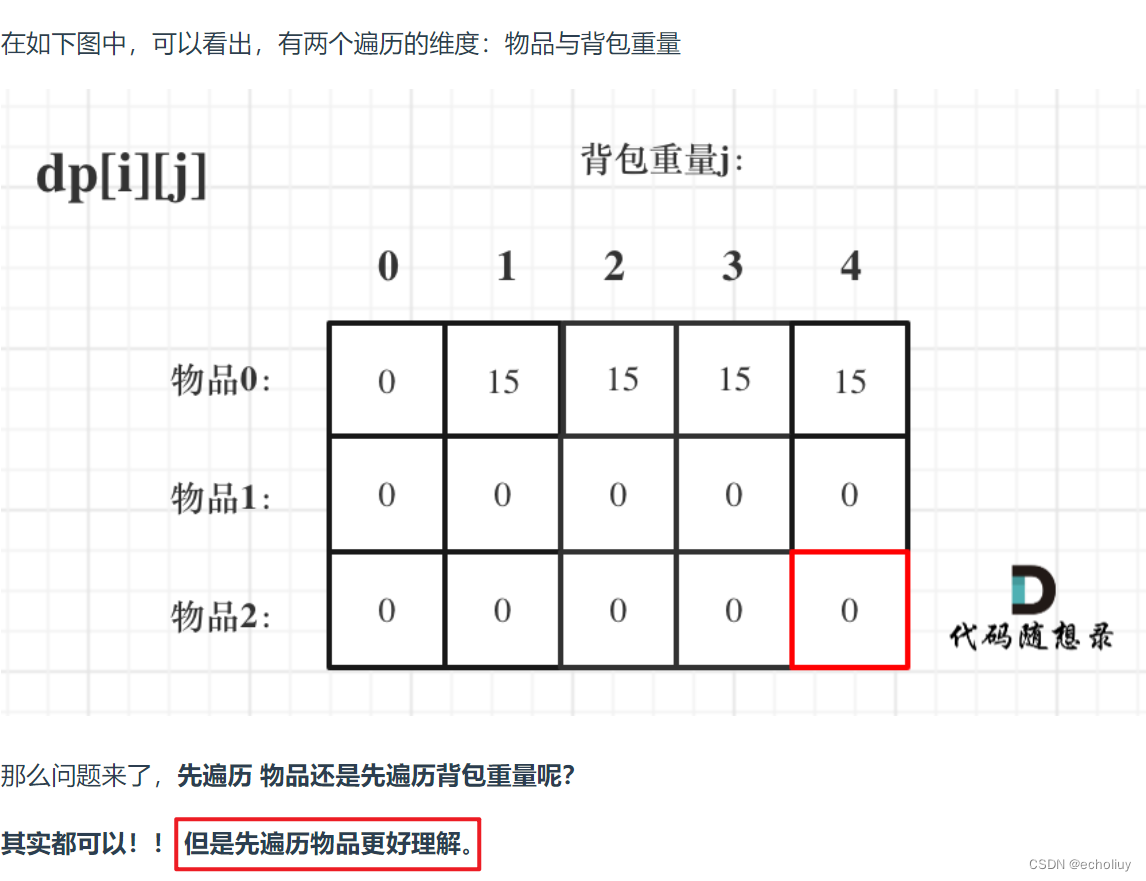
1.确定dp数组
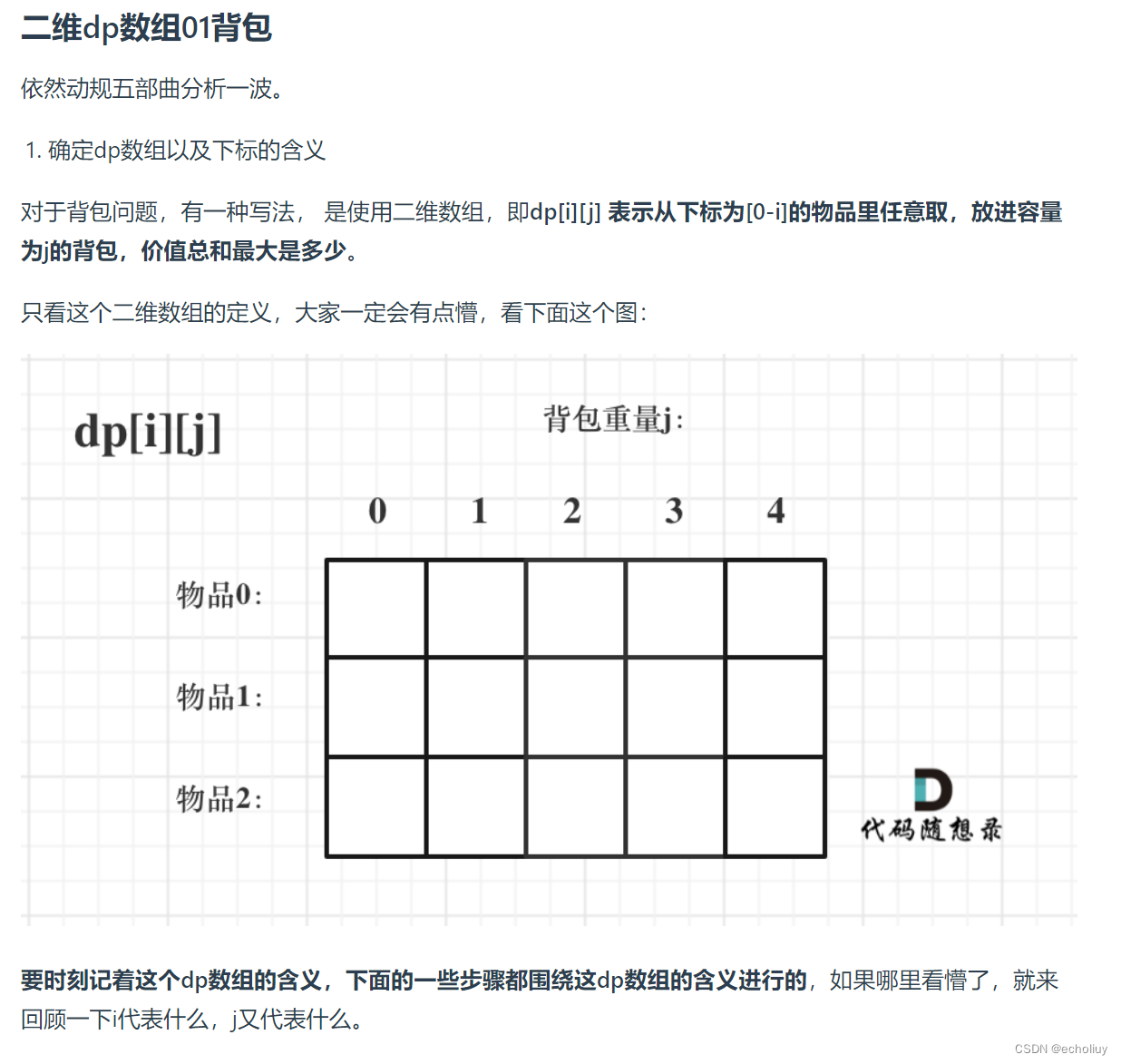
2、确定递推公式

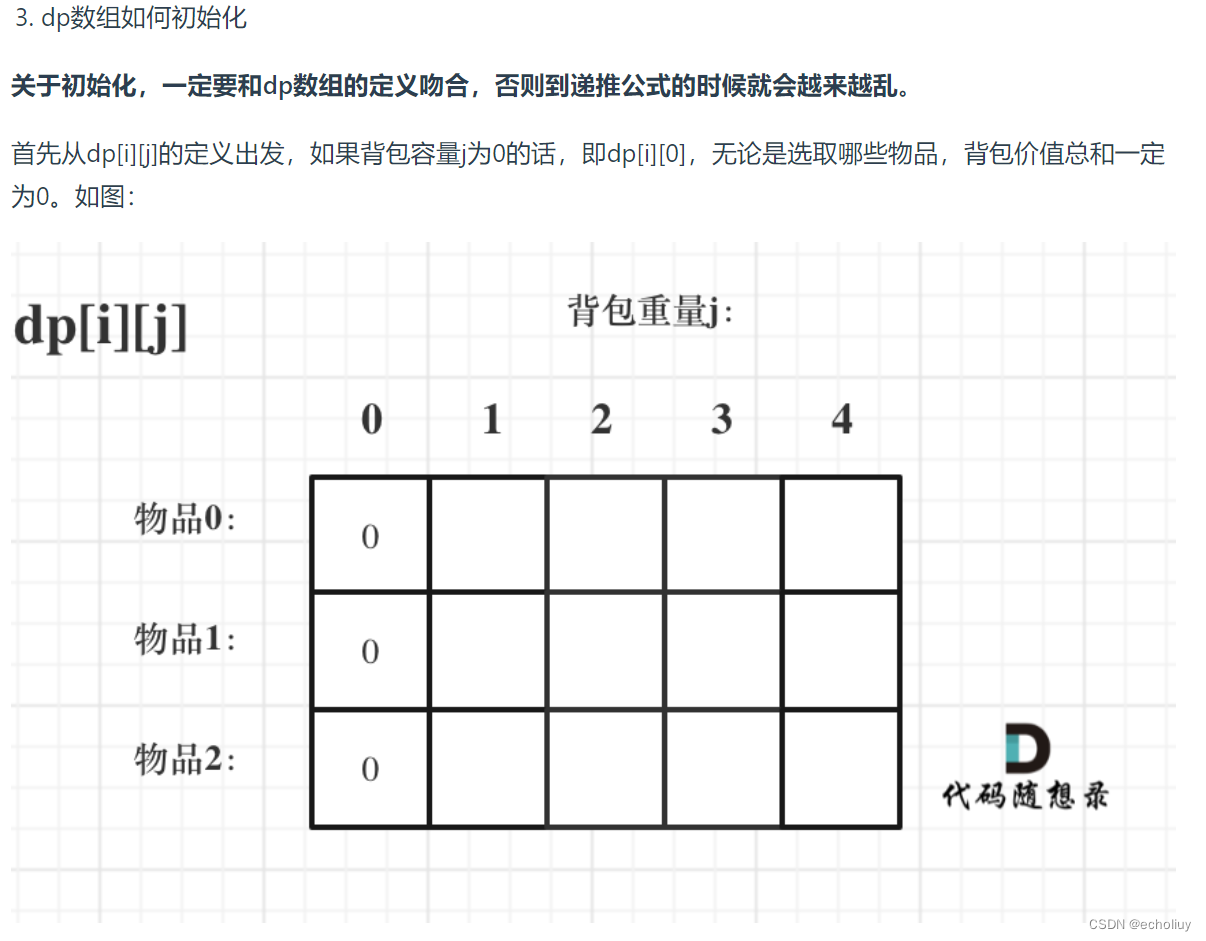
3、初始化dp数组
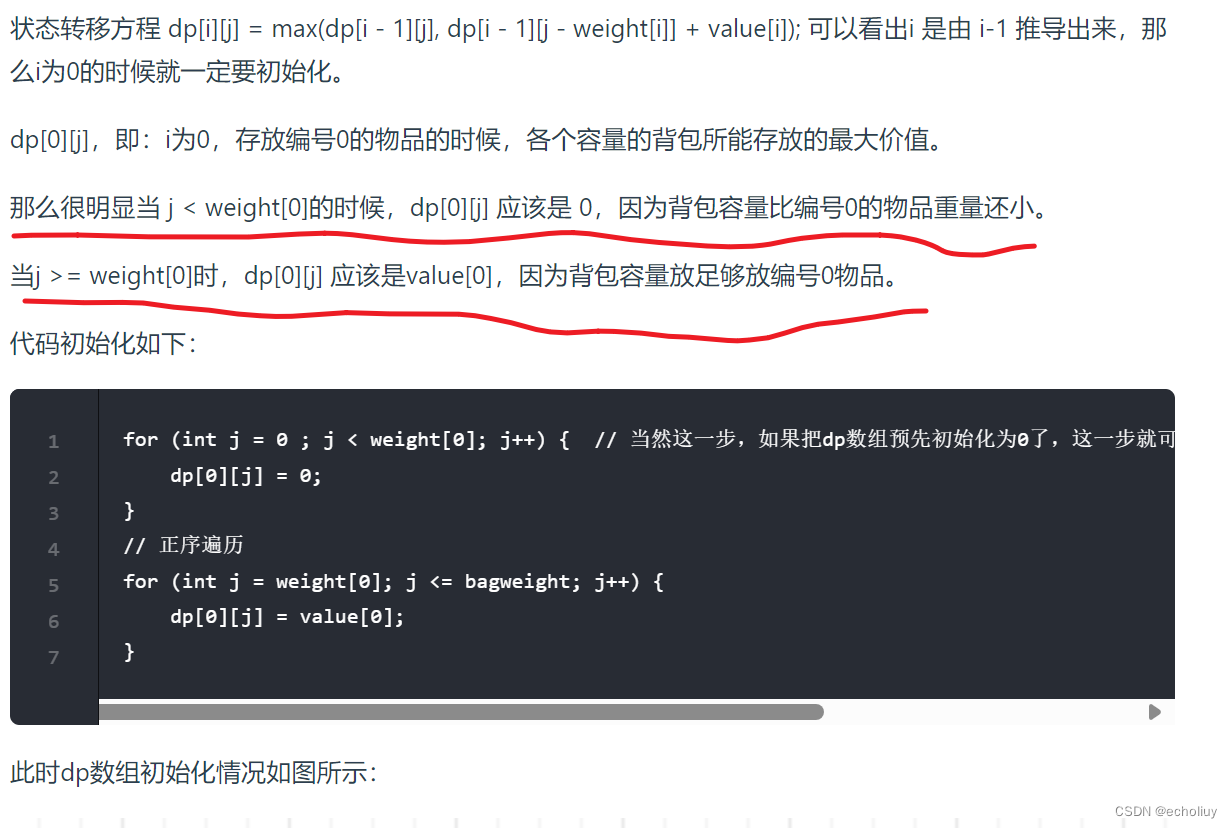
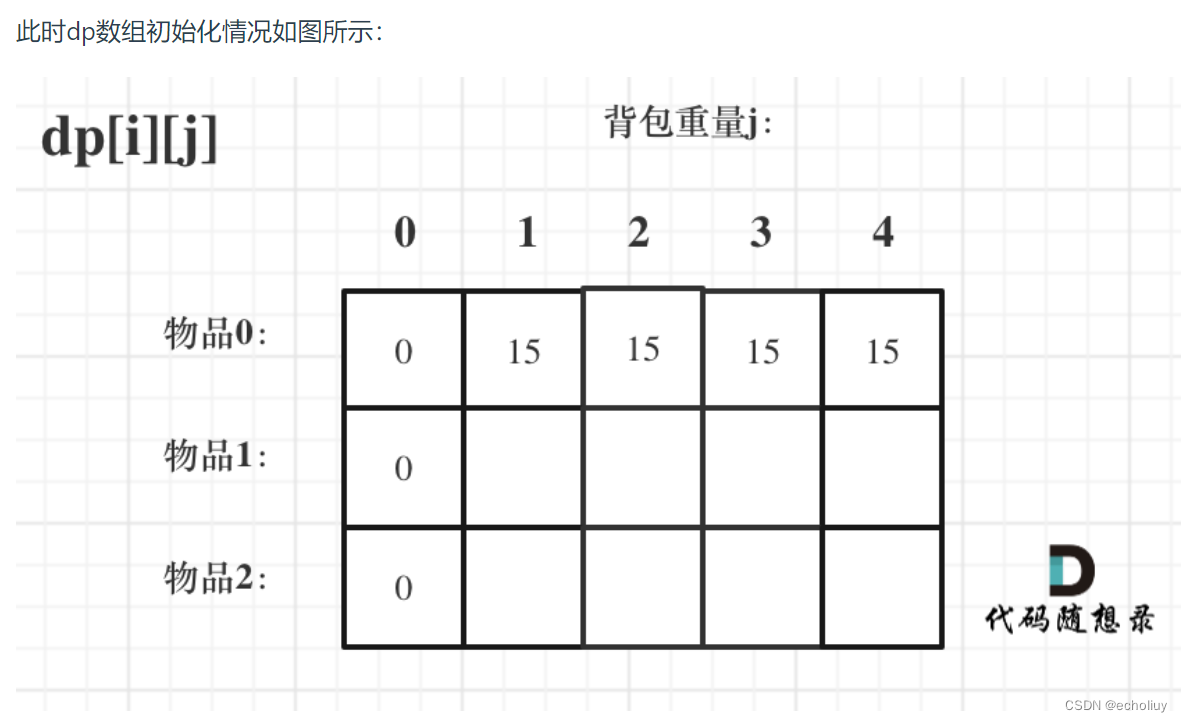

4、循环
代码:
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int m=sc.nextInt();
int n=sc.nextInt();
int[] weight=new int[m];
for(int i=0;i<m;i++){
weight[i]=sc.nextInt();
}
int[] values=new int[m];
for(int i=0;i<m;i++){
values[i]=sc.nextInt();
}
int[][] dp=new int[m][n+1];
for(int j=weight[0];j<=n;j++){
dp[0][j]=values[0];//其他初始化为0
}
//先物品再体积
for(int i=1;i<m;i++){
for(int j=1;j<=n;j++){
if(j<weight[i]){
dp[i][j]=dp[i-1][j];
}
else{
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+values[i]);
}
}
}
System.out.println(dp[m-1][n]);
}
}
解法二-01背包问题-滚动数组

五部曲1:定义dp

二、递推公式

三、初始化

四、循环顺序
看完了提个小建议,解释倒序遍历那一部分用一句话解释可能更好,比如“列表后面的值需要通过与前面的值比较确定,因此要先处理”。举了个例子反倒会让观众的关注点从逻辑本身转移到数字和具体的计算上


代码:
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int m=sc.nextInt();
int n=sc.nextInt();
int[] weight=new int[m];
for(int i=0;i<m;i++){
weight[i]=sc.nextInt();
}
int[] values=new int[m];
for(int i=0;i<m;i++){
values[i]=sc.nextInt();
}
int[] dp=new int[n+1];
// for(int j=weight[0];j<=n;j++){//i=0在这里初始化
// dp[0][j]=values[0];//其他初始化为0
// }
//先物品再体积
for(int i=0;i<m;i++){
for(int j=n;j>= weight[i];j--){
dp[j]=Math.max(dp[j],dp[j-weight[i]]+values[i]);
}
}
System.out.println(dp[n]);
}
}
698. 划分为k个相等的子集

题解:
力扣题解
代码:
class Solution {
public static int[] numUsed;
public boolean canPartitionKSubsets(int[] nums, int k) {
numUsed = new int[nums.length];
Arrays.sort(nums);//排列
// int sum = Arrays.stream(nums).sum();
int sum=0;
for(int i:nums){
sum+=i;
}
//1.不能整分 2.最大的数大于均分的数值 ->都返回false
if (sum % k != 0 || nums[nums.length - 1] > sum / k) return false;
return divideGroups(nums, nums.length - 1, sum / k, 0, k);//从后向前找
}
public boolean divideGroups(int[] nums, int start, int target, int current, int k) {
if (k == 1) return true; // 分组操作执行k-1次之后,最后剩余的元素,就是最后一组了,不需要再匹配
// 分组操作执行k-1次后,最后剩余的元素,就是最后一组了,不需要再匹配
if (current == target) return divideGroups(nums, nums.length - 1, target, 0, k - 1);
for (int i = start; i >= 0; i--) {
if (numUsed[i] == 1 || current + nums[i] > target) continue; // 被使用的元素,不能再次使用;总和大于目标值,也不能使用
numUsed[i] = 1; // 标记占用
if (divideGroups(nums, i - 1, target, current + nums[i], k)) return true;
numUsed[i] = 0; // 撤销标记
// 去重
while (i > 0 && nums[i - 1] == nums[i]) i--; // 例如“12333333...”,假如最右侧的“3”这个值没有匹配上,那么它左侧的剩余五个“3”都不需要再匹配了。
}
return false;
}
}
● 416. 分割等和子集

思路:-自己没思路

动归五部曲-1.确定dp数组以及下标的含义

2.递推公式
- dp[j]=Math.max(dp[j],dp[j-weight[i]]+values[i]) → dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3. dp数组如何初始化
都为0
4.确定遍历顺序
物品正序 重量逆序
5. dp数组

代码:
class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
for(int i:nums){
sum+=i;
}
if(sum%2!=0)return false;
int target=sum/2;
int[] dp=new int[target+1];
for(int i=0;i<nums.length;i++){
for(int j=target;j>=nums[i];j--){
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
if(dp[target]==target)return true;//剪枝
}
return dp[target]==target;
}
}