文章目录
- 归一化
- 批量归一化
- 预测阶段
- 测试阶段
- γ和β(注意)
- 举例
- 层归一化
- 前向传播
- 反向传播
归一化
批量归一化
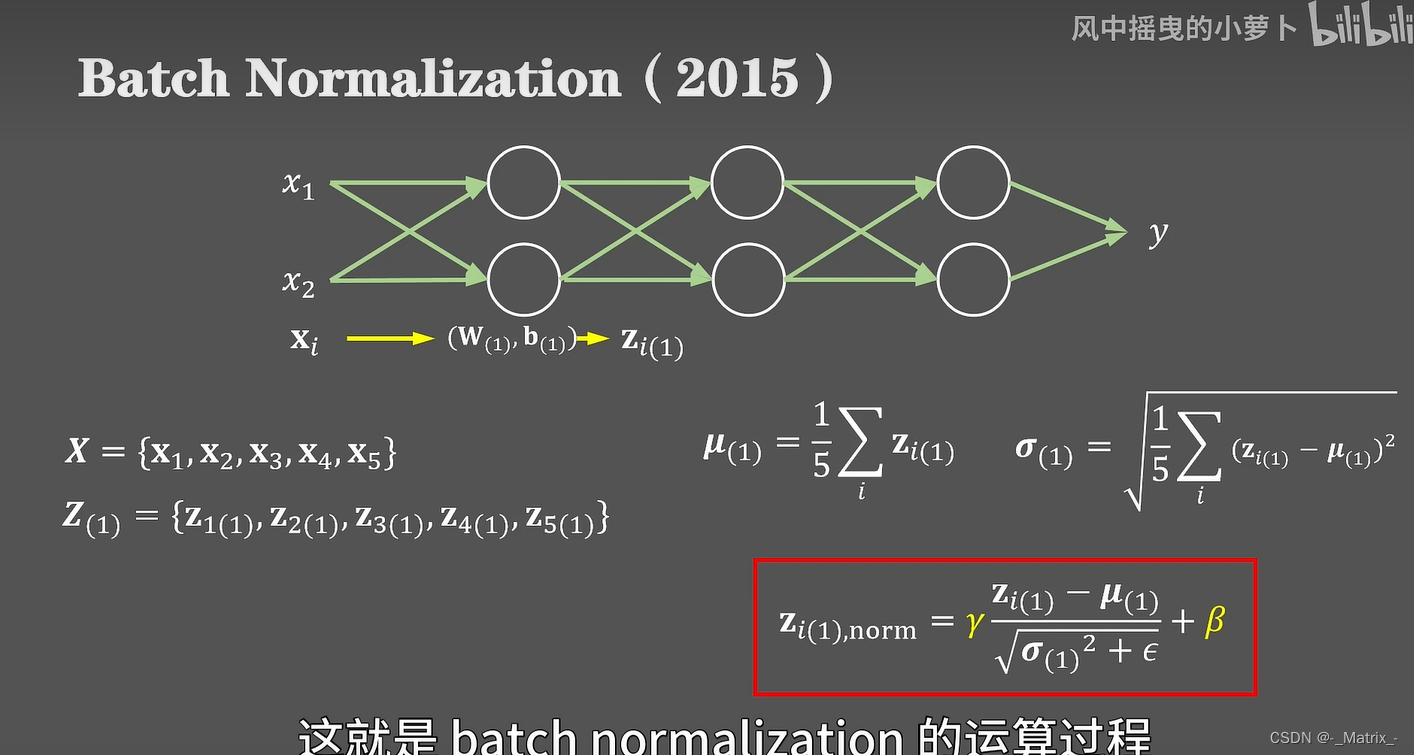


(Batch Normalization)在训练过程中的数学公式可以概括如下:
给定一个小批量数据 B = { x 1 , x 2 , … , x m } B = \{x_1, x_2, \ldots, x_m\} B={x1,x2,…,xm},其中 m m m 是批次的大小。
-
计算均值:计算小批量数据的均值。
μ B = 1 m ∑ i = 1 m x i \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i μB=m1∑i=1mxi -
计算方差:计算小批量数据的方差。
σ B 2 = 1 m ∑ i = 1 m ( x i − μ B ) 2 \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 σB2=m1∑i=1m(xi−μB)2 -
归一化:使用均值和方差对小批量数据进行标准化。
x ^ i = x i − μ B σ B 2 + ϵ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} x^i=σB2+ϵxi−μB
其中, ϵ \epsilon ϵ 是一个小的常数,用于确保分母不为零。 -
缩放和平移:使用可学习的参数伽玛 γ \gamma γ和贝塔 β \beta β来缩放和平移标准化的数据。
y i = γ x ^ i + β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β
其中, γ \gamma γ 和 β \beta β 是可学习的参数,用于调整归一化的缩放和平移。
这样做可以让模型有更大的灵活性,因为它可以学习到每个特征或通道应该如何被归一化。
预测阶段
在推断阶段,使用整个训练集的均值和方差(通常是移动平均)来替代小批量的均值和方差。这确保了网络在推断时的行为与训练时的行为更加一致。
在批量归一化中,移动平均均值和方差是在训练阶段计算并用于预测阶段的归一化过程。移动平均的计算通常使用指数移动平均(EMA)或其他平滑方法。下面是计算移动平均均值和方差的一般过程:
-
初始化:在训练开始时,初始化移动平均均值和方差为零或其他初始值。
-
计算当前批次的均值和方差:对于每个训练批次,计算该批次数据的均值和方差。
-
更新移动平均:使用当前批次的均值和方差以及之前的移动平均值来更新移动平均。通常,这可以通过下面的公式完成:
移动平均均值 = m o m e n t u m × 移动平均均值 + ( 1 − m o m e n t u m ) × 当前批次均值 \text{移动平均均值} = momentum \times \text{移动平均均值} + (1 - momentum) \times \text{当前批次均值} 移动平均均值=momentum×移动平均均值+(1−momentum)×当前批次均值
移动平均方差 = m o m e n t u m × 移动平均方差 + ( 1 − m o m e n t u m ) × 当前批次方差 \text{移动平均方差} = momentum \times \text{移动平均方差} + (1 - momentum) \times \text{当前批次方差} 移动平均方差=momentum×移动平均方差+(1−momentum)×当前批次方差其中, m o m e n t u m momentum momentum 是一个超参数,通常在 0 到 1 之间,通常设置为接近 1 的值(例如 0.9),决定了移动平均的平滑程度。较小的 m o m e n t u m momentum momentum 值会使移动平均更关注最近的批次,而较大的值则会使其更平滑。
-
使用当前mini-batch的均值和方差对数据进行归一化,并通过可学习的参数 γ γ γ 和 β β β 进行缩放和偏移。
BN ( x i ) = γ ( x i − μ B σ B 2 + ϵ ) + β \text{BN}(x_i) = \gamma \left( \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \right) + \beta BN(xi)=γ(σB2+ϵxi−μB)+β
测试阶段
在测试阶段,使用训练期间计算的运行均值和方差进行归一化:
BN ( x i ) = γ ( x i − μ running σ running 2 + ϵ ) + β \text{BN}(x_i) = \gamma \left( \frac{x_i - \mu_{\text{running}}}{\sqrt{\sigma_{\text{running}}^2 + \epsilon}} \right) + \beta BN(xi)=γ(σrunning2+ϵxi−μrunning)+β
通过这种方式,批量归一化可以在测试阶段更稳定和准确地归一化数据。
γ和β(注意)
在批量归一化中, γ \gamma γ 和 β \beta β 不是单一的数值,而是可以学习的参数向量。其维度与正在被归一化的数据的维度相同。这样可以确保每个特征有其自己的 γ \gamma γ 和 β \beta β 参数,可以独立地进行缩放和偏移。
具体来说:
- 在全连接层中,如果该层有 d d d 个神经元,那么 γ \gamma γ 和 β \beta β 将是 d d d 维向量。
- 在卷积层中,如果卷积层有 c c c 个通道,那么 γ \gamma γ 和 β \beta β 将是 c c c 维向量,每个通道有一个 γ \gamma γ 和 β \beta β 值。
举例
以下是按照10个样本,20个特征,计算移动平均方差的步骤:
-
初始化移动平均方差:在训练开始时,为每个特征初始化一个移动平均方差值。可以将其设置为零或其他初始值。你将得到一个具有20个元素的移动平均方差向量。
-
对于每个批次:对于每个训练批次,执行以下步骤:
a. 计算当前批次的方差:按照之前的方法计算当前批次的方差。结果将是一个包含20个方差值的向量。
b. 更新移动平均方差:使用以下公式来更新每个特征的移动平均方差:
移动平均方差 j = m o m e n t u m × 移动平均方差 j + ( 1 − m o m e n t u m ) × 当前批次方差 j \text{移动平均方差}_j = momentum \times \text{移动平均方差}_j + (1 - momentum) \times \text{当前批次方差}_j 移动平均方差j=momentum×移动平均方差j+(1−momentum)×当前批次方差j
其中, m o m e n t u m momentum momentum 是一个超参数,通常在 0 到 1 之间,表示移动平均的平滑程度。这个过程会为每个特征更新移动平均方差。
- 预测时使用:在预测阶段,使用最终计算的移动平均方差向量来归一化新样本。
在批量归一化中,每个特征都有其自己的移动平均均值和移动平均方差。这些值是在训练过程中单独计算和跟踪的。
由于不同的特征可能具有不同的尺度和分布,因此为每个特征单独计算均值和方差是有意义的。这样可以确保在整个训练集中,每个特征都被归一化到具有相同的均值和方差,从而有助于提高训练的稳定性和效率。
层归一化
(Layer Normalization)是一种归一化技术,常用于深度学习模型中。下面我们来详细了解层归一化的前向传播和反向传播过程。
前向传播
给定输入向量 x x x,层归一化的前向传播包括以下步骤:
-
计算均值:计算输入 x x x 中所有特征的均值。
μ = 1 d ∑ i = 1 d x i \mu = \frac{1}{d} \sum_{i=1}^{d} x_i μ=d1∑i=1dxi -
计算方差:计算输入 x x x 中所有特征的方差。
σ 2 = 1 d ∑ i = 1 d ( x i − μ ) 2 \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 σ2=d1∑i=1d(xi−μ)2 -
归一化:使用均值和方差对输入 x x x 进行标准化。
x ^ i = x i − μ σ 2 + ϵ \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} x^i=σ2+ϵxi−μ -
缩放和平移:使用可学习的参数伽玛 γ \gamma γ和贝塔 β \beta β来缩放和平移标准化的数据。
y i = γ x ^ i + β y_i = \gamma \hat{x}_i + \beta yi=γx^i+β
反向传播
反向传播需要计算损失函数 L L L 对输入 x x x、伽玛 γ \gamma γ和贝塔 β \beta β的偏导数。以下是相关的偏导数计算:
-
对伽玛和贝塔的偏导数:
∂ L ∂ γ = ∑ i = 1 d ∂ L ∂ y i x ^ i , ∂ L ∂ β = ∑ i = 1 d ∂ L ∂ y i \frac{\partial L}{\partial \gamma} = \sum_{i=1}^{d} \frac{\partial L}{\partial y_i} \hat{x}_i, \quad \frac{\partial L}{\partial \beta} = \sum_{i=1}^{d} \frac{\partial L}{\partial y_i} ∂γ∂L=∑i=1d∂yi∂Lx^i,∂β∂L=∑i=1d∂yi∂L -
对归一化输入的偏导数:
∂ L ∂ x ^ i = ∂ L ∂ y i γ \frac{\partial L}{\partial \hat{x}_i} = \frac{\partial L}{\partial y_i} \gamma ∂x^i∂L=∂yi∂Lγ -
对方差的偏导数:
∂ L ∂ σ 2 = 1 2 ∑ i = 1 d ∂ L ∂ x ^ i 1 σ 2 + ϵ ( x i − μ ) \frac{\partial L}{\partial \sigma^2} = \frac{1}{2} \sum_{i=1}^{d} \frac{\partial L}{\partial \hat{x}_i} \frac{1}{\sqrt{\sigma^2 + \epsilon}} (x_i - \mu) ∂σ2∂L=21∑i=1d∂x^i∂Lσ2+ϵ1(xi−μ) -
对均值的偏导数:
∂ L ∂ μ = ∑ i = 1 d ∂ L ∂ x ^ i − 1 σ 2 + ϵ − 2 d ∂ L ∂ σ 2 ( μ − x i ) \frac{\partial L}{\partial \mu} = \sum_{i=1}^{d} \frac{\partial L}{\partial \hat{x}_i} \frac{-1}{\sqrt{\sigma^2 + \epsilon}} - \frac{2}{d} \frac{\partial L}{\partial \sigma^2} (\mu - x_i) ∂μ∂L=∑i=1d∂x^i∂Lσ2+ϵ−1−d2∂σ2∂L(μ−xi) -
对输入的偏导数:
∂ L ∂ x i = ∂ L ∂ x ^ i 1 σ 2 + ϵ + 2 d ∂ L ∂ σ 2 ( x i − μ ) + 1 d ∂ L ∂ μ \frac{\partial L}{\partial x_i} = \frac{\partial L}{\partial \hat{x}_i} \frac{1}{\sqrt{\sigma^2 + \epsilon}} + \frac{2}{d} \frac{\partial L}{\partial \sigma^2} (x_i - \mu) + \frac{1}{d} \frac{\partial L}{\partial \mu} ∂xi∂L=∂x^i∂Lσ2+ϵ1+d2∂σ2∂L(xi−μ)+d1∂μ∂L
这些偏导数可以通过链式法则和上述前向传播步骤计算,从而实现层归一化的反向传播。这样就可以在训练过程中更新模型参数,并通过梯度下降或其他优化算法进行优化。



![[树形DP] 树的最大独立集](https://img-blog.csdnimg.cn/direct/57445544106240a5bcc4731f4bf37685.png)