文章目录
- 什么是m估计
- 怎么求解m估计呢?
- Huber函数时的线性m估计
什么是m估计
自20世纪60年代稳健统计建立以来,在国内外众多学者的研究之下,诞生了一系列稳健统计重要理论和成果。其中最主要且广泛使用的稳健统计有以下三类:
- L-estimators (linear combinations of order statistics of the observations);
- R-estimators (estimator based on waste ranking);
- M-estimators (generalizations of a Maximum Likelihood estimator)
m估计可以翻译为通用的最大似然估计,其是由Huber提出的,是最常用的稳健统计方法。其标准形式为:
min
S
(
x
j
)
=
min
∑
i
=
1
n
ρ
(
r
i
)
(1)
\min{S(x_j)}=\min \sum_{i=1}^n \rho(r_i)\tag{1}
minS(xj)=mini=1∑nρ(ri)(1)
S
为目标函数,
x
j
为估计参数,
ρ
(
)
为残差函数
,
r
i
为残差
S为目标函数,x_j为估计参数,\rho()为残差函数,r_i为残差
S为目标函数,xj为估计参数,ρ()为残差函数,ri为残差。
ρ
(
)
残差函数需要满足以下性质:
\rho()残差函数需要满足以下性质:
ρ()残差函数需要满足以下性质:
连续性,偶函数,非负性,通过原点,在正半轴单调递增。
提出了很多的残差函数:Huber, l1-l2, Fair, Cauchy, Geman-McClure, Welsch, and Tukey estimators等等。
怎么求解m估计呢?
通常使用迭代加权最小二乘(Iterative Reweight Least Square, IRLS,有时也叫迭代选权最小二乘?)求解m估计。具体过程如下:
要求解的式1,一般需要对其求一阶偏导:
∂
S
∂
x
j
=
∑
i
=
1
m
d
ρ
(
r
i
)
d
r
i
∂
r
i
∂
x
j
=
0
,
j
=
0
,
…
,
n
(2)
\frac{\partial S}{\partial x_j}=\sum_{i=1}^m \frac{d \rho\left(r_i\right)}{d r_i} \frac{\partial r_i}{\partial x_j}=0, j=0, \ldots, n\tag{2}
∂xj∂S=i=1∑mdridρ(ri)∂xj∂ri=0,j=0,…,n(2)令
ρ
(
r
)
\rho(r)
ρ(r) 的一阶导数(梯度)为
ψ
(
r
)
=
a
ρ
(
r
)
d
r
,
ψ
(
r
)
\psi(r)=\frac{a \rho(r)}{d r} , \psi(r)
ψ(r)=draρ(r),ψ(r) 在M估计中被叫做影响力函数(Influence Function);
令
w
(
r
)
=
ψ
(
r
)
r
w(r)=\frac{\psi(r)}{r}
w(r)=rψ(r) ,该函数在M估计中被叫做权重函数(Weight Function);
将
(
2
)
(2)
(2) 变形:
∂
S
∂
x
j
=
∑
i
=
1
m
d
ρ
(
r
i
)
d
r
i
∂
r
i
∂
x
j
=
∑
i
=
1
m
ψ
(
r
i
)
∂
r
i
∂
x
j
=
∑
i
=
1
m
w
(
r
i
)
r
i
∂
r
i
∂
x
j
=
0
(3)
\frac{\partial S}{\partial x_j}=\sum_{i=1}^m \frac{d \rho\left(r_i\right)}{d r_i} \frac{\partial r_i}{\partial x_j}=\sum_{i=1}^m \psi\left(r_i\right) \frac{\partial r_i}{\partial x_j}=\sum_{i=1}^m w\left(r_i\right) r_i \frac{\partial r_i}{\partial x_j}=0\tag{3}
∂xj∂S=i=1∑mdridρ(ri)∂xj∂ri=i=1∑mψ(ri)∂xj∂ri=i=1∑mw(ri)ri∂xj∂ri=0(3)
如果
w
(
r
i
)
w\left(r_i\right)
w(ri) 是一个常数,比如用上一次迭代优化的结果
x
k
x^k
xk 的残差替换:
∑
i
=
1
m
w
(
r
i
k
)
r
i
∂
r
i
∂
x
j
=
0
(4)
\sum_{i=1}^m w\left(r_i^k\right) r_i \frac{\partial r_i}{\partial x_j}=0\tag{4}
i=1∑mw(rik)ri∂xj∂ri=0(4)
式(4)等价于 argmin x 1 2 ∑ i = 1 m w i ( r i k ) . r i ( x ) 2 \underset{x}{\operatorname{argmin}} \frac{1}{2} \sum_{i=1}^m w_i\left(r_i^k\right). r_i(x)^2 xargmin21∑i=1mwi(rik).ri(x)2,即等价于加权最小二乘求解问题。由于权重函数的数值不是固定的,因此我们很自然地想到通过多次迭代求解加权最小二乘来得到的最终的 x x x.因此迭代加权最小二乘算法步骤如下:
- (1)获取 x x x初值,线性最小二乘可以通过 x 0 = ( X T X ) − 1 X T Y x_0=(X^TX)^{-1}X^TY x0=(XTX)−1XTY,非线性问题,可以通过别的方式获得
- (2)利用得到的 x k x_k xk计算 ψ ( r ) \psi(r) ψ(r),再计算 w ( r ) w(r) w(r)
- (3)利用权重求解 argmin x 1 2 ∑ i = 1 m w i ( r i k ) . r i ( x ) 2 \underset{x}{\operatorname{argmin}} \frac{1}{2} \sum_{i=1}^m w_i\left(r_i^k\right). r_i(x)^2 xargmin21∑i=1mwi(rik).ri(x)2,获得新的 x k + 1 x_{k+1} xk+1.非线性问题可以通过梯度法,牛顿高斯法,牛顿法,共轭梯度法或者lm方法求解,线性问题可以利用 x k + 1 = ( X T W X ) − 1 X T W Y , W 为权重 x_{k+1}=(X^TWX)^{-1}X^TWY,W为权重 xk+1=(XTWX)−1XTWY,W为权重
- (4)若 ∣ x k + 1 − x k ∣ < ε |x_{k+1}-x_{k}|<\varepsilon ∣xk+1−xk∣<ε或者大于迭代次数,终止迭代,否则返回第二步
Huber函数时的线性m估计
对于Huber而言:
ρ
(
r
)
=
{
r
2
2
,
∣
r
∣
≤
k
k
∣
r
∣
−
k
2
2
,
∣
r
∣
>
k
\rho(r)= \begin{cases}\frac{r^2}{2}, & |r| \leq k \\ k|r|-\frac{k^2}{2}, & |r|>k\end{cases}
ρ(r)={2r2,k∣r∣−2k2,∣r∣≤k∣r∣>k
φ
(
r
)
\varphi(\mathrm{r})
φ(r) 为
ρ
(
r
)
\rho(\mathrm{r})
ρ(r) 的导数:
φ
(
r
)
=
{
−
k
r
<
−
k
r
∣
r
∣
≤
k
k
r
>
k
\varphi(r)=\left\{\begin{array}{cc} -k & r<-k \\ r & |r| \leq k \\ k & r>k \end{array}\right.
φ(r)=⎩
⎨
⎧−krkr<−k∣r∣≤kr>k
权重函数
w
(
r
)
w(r)
w(r):
w
(
r
)
=
{
−
k
r
r
<
−
k
1
∣
r
∣
≤
k
k
r
r
>
k
w(r)=\left\{\begin{array}{cc} \frac{-k}{r} & r<-k \\ 1 & |r| \leq k \\ \frac{k}{r} & r>k \end{array}\right.
w(r)=⎩
⎨
⎧r−k1rkr<−k∣r∣≤kr>k
已知线性函数的自变量为
x
i
x_i
xi,因变量为
y
i
y_i
yi,设线性函数为
a
x
+
b
=
0
ax+b=0
ax+b=0,有残差
r
i
=
a
x
i
+
b
−
y
i
r_i=ax_i+b-y_i
ri=axi+b−yi,令:
A
=
[
x
1
1
x
2
1
.
.
.
x
i
1
.
.
.
x
n
1
]
,
Y
=
[
y
1
y
2
.
.
.
y
i
.
.
.
y
n
]
,
A= \begin{bmatrix} x_1&1\\ x_2&1\\ ...\\ x_i&1\\ ...\\ x_n&1 \end{bmatrix}, Y=\begin{bmatrix} y_1\\ y_2\\ ...\\ y_i\\ ...\\ y_n \end{bmatrix},
A=
x1x2...xi...xn1111
,Y=
y1y2...yi...yn
,
有:
r
=
A
[
a
,
b
]
T
−
Y
r=A[a,b]^T-Y
r=A[a,b]T−Y
对于最小二乘直接解为:
a
,
b
=
(
X
T
X
)
−
1
X
T
Y
a,b=(X^TX)^{-1}X^TY
a,b=(XTX)−1XTY,对于加权最小二乘直接解为:
a
,
b
=
(
X
T
W
X
)
−
1
X
T
W
Y
,
W
a,b=(X^TWX)^{-1}X^TWY,W
a,b=(XTWX)−1XTWY,W为权重.
codes:
#include <iostream>
#include<Eigen/Core>
#include<Eigen/Dense>
int main()
{
const int size = 7;
const double k = 1.5;//huber超参数
//y=2x+1
double x[size]{ 1.0,2.1,2.9,5.01,8.093,6.0,3.0 };
double y[size]{ 3.02,4.97,7.1,10.88,17.06 ,2.0,17.6};
//初值
Eigen::MatrixXd A = Eigen::MatrixXd::Zero(size, 2);
Eigen::MatrixXd Y = Eigen::MatrixXd::Zero(size, 1);
for (size_t i = 0; i < size; i++)
{
A(i, 0) = x[i];
A(i, 1) = 1;
Y(i, 0) = y[i];
}
Eigen::MatrixXd ab0 = (A.transpose()*A).inverse()*A.transpose()*Y;
std::cout << ab0 << std::endl;
//残差
Eigen::MatrixXd R = Eigen::MatrixXd::Zero(size, 1);
Eigen::MatrixXd W = Eigen::MatrixXd::Zero(size, size);//对角阵
//初值
double a_k = ab0(0, 0);
double b_k = ab0(1, 0);
int iter_times = 1;
while (true)
{
for (size_t j = 0; j < size; j++)
{
//计算残差
R(j, 0) = a_k * x[j] + b_k - y[j];
//计算Huber权重
if (R(j, 0)<-1.0*k)
{
W(j, j) = -1.0*k / R(j, 0);
}
else if (std::abs(R(j, 0)) < k)
{
W(j, j) = 1.0;
}
else if (R(j, 0) > k)
{
W(j, j) = k/ R(j, 0);
}
}
Eigen::MatrixXd ab= (A.transpose()*W*A).inverse()*A.transpose()*W*Y;
++iter_times;
if (std::abs(ab(0,0)-a_k)<1e-3&&std::abs(ab(1, 0) - b_k) < 1e-3)
{
std::cout << ab << std::endl;
break;
}
else if(iter_times>20)
{
std::cout << ab << std::endl;
break;
}
else
{
a_k=ab(0,0);
b_k = ab(1, 0);
}
}
std::cout << "Hello World!\n";
std::cout << iter_times << std::endl;
}
结果:
a0=1.09263
b0=4.56053
a=1.83641
b=1.58977
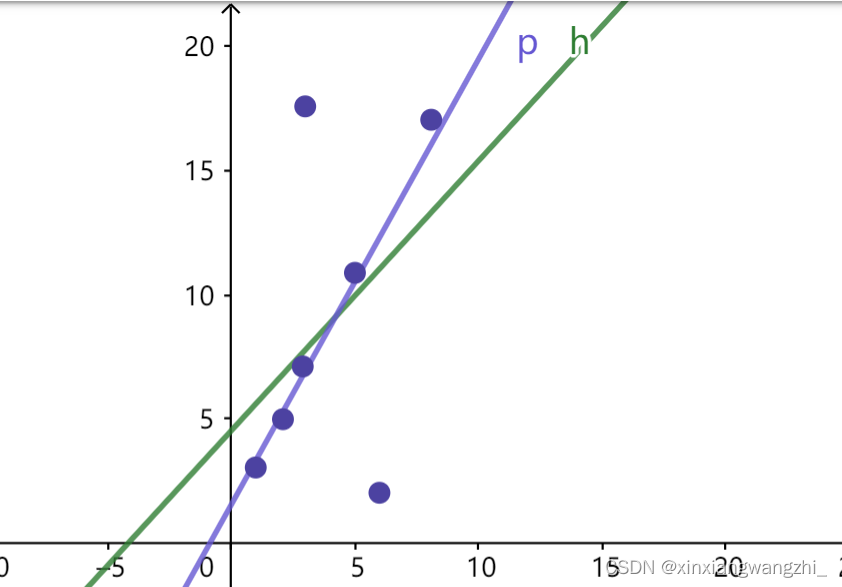
直线h为直接最小二乘计算的结果,直线p为m估计的结果。
参考:
1
2
3
4
《A review on robust M-estimators for regression analysis》
《ROBUST ESTIMATION IN ROBOT VISION AND PHOTOGRAMMETRY: A NEW MODEL AND ITS APPLICATIONS》