动态规划课堂1-----斐波那契数列模型

动态规划的概念：

动态规划的解法流程：

题目: 第 N 个泰波那契数

解法（动态规划）

代码：

优化：

题目：最小花费爬楼梯

解法（动态规划）

解法1：

解法2：

题目：解码方法

解法（动态规划）

结语：

动态规划：斐波那契数列模型

动态规划的概念：

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

动态规划的解法流程：

1.状态表示

dp问题的基础，自己要确定dp表每一个下标值的含义，这是用动态规划解决问题的第一步，只有把这一步确定了再去推出下面的状态转移方程，第一第二步完成后那么dp问题就已经解决了99%因为剩下的345就是处理边界和一些细节问题。

2.状态转移方程

推出状态转移方程可以说是dp问题最难的一步，如果在选定的状态表示下推不出状态转移方程，那么可能要换一个状态表示，因为状态表示可能是错误的。

3.初始化

一般初始化dp[0]和dp[1] .

4.填表顺序

一般有从左向右和从右先左，这取决于题目（覆盖问题）。

5.返回值

最后的返回值（不一定是dp[n]）.

由于是算法只讲知识点是远远不够的，故下面我会用例题来帮助大家理解（例题的链接会在最后给出）。

到这一些基本概念就讲解完毕下面开始用题目要带友友更加深入学习。

题目: 第 N 个泰波那契数

题目链接1137. 第 N 个泰波那契数

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2.

给你整数，请返回第 n 个泰波那契数 Tn 的值。

解法（动态规划）

1. 状态表示：

根据题目来推出状态表示，后面的大部分题目是要经验+题目来推出的

这道题可以「根据题目的要求」直接定义出状态表示：

dp[i] 表示：第i 个泰波那契数的值。

2.状态转移方程

dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]。

3.初始化

从我们的递推公式可以看出， dp[i] 在 i = 0 以及i = 1 的时候是没有办法进行推导的，因为dp[-2] 或dp[-1] 不是⼀个有效的数据。因此我们需要在填表之前，将0, 1, 2 位置的值初始化。题目中已经告诉我们dp[0] = 0, dp[1] = dp[2] = 1 。（处理一些边界问题）

4.填表顺序

毫无疑问是「从左往右」。

5.返回值：

应该返回dp[n] 的值。

代码：

dp问题的代码编写流程一般比较固定分为1.创建dp表,2.初始化,3.填表,4.返回值.

最上面两个if用来解决边界问题。

class Solution {
    public int tribonacci(int n) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        int[] dp = new int[n + 1];
        if(n == 0){
            return 0;
        }
        if(n == 1 || n == 2){
            return 1;
        }
        dp[0] = 0;dp[2] = dp[1] = 1;

        for(int i = 3;i <= n;i++){
            dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];
        }
        return dp[n];

    }
}

优化：

下面动图来自力扣。

一般是利用滚动数组优化（可以是一个小数组也可以是几个变量）

代码如下：

其实就是把表变成几个变量把空间复杂度降低到O（1）。

class Solution {
    public int tribonacci(int n) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        if(n == 0){
            return 0;
        }
        if(n == 1 || n == 2){
            return 1;
        }
        int a = 0,b = 1, c = 1,d = 0;
        for(int i = 3;i <= n;i++){
            d = a + b + c;
            a = b;
            b = c;
            c = d;
        }
        return d;

    }
}

类似题：和上面那题类似给大家练手。

三步问题

参考代码如下：

其中dp[i] 表示：到达i位置时，⼀共有多少种方法。

通过分析知道第i步的方法为前三步方法的总和故状态转移方程为dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]。

class Solution {
    public int waysToStep(int n) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        //处理一下边界问题
        int MOD = (int)1e9 + 7;
        if(n == 1 || n == 2){
            return n;
        }
        if(n == 3){
            return 4;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;dp[2] = 2;dp[3] = 4;
        for(int i = 4;i <= n;i++){
            dp[i] = ((dp[i - 3] + dp[i - 2]) % MOD+ dp[i - 1]) % MOD;
        } 
        return dp[n];
    }
}

题目：最小花费爬楼梯

题目链接：使用最小花费爬楼梯

注意这里的顶部不是数组的最后一个位置，而是在数组最后一个位置再后面一个。

解法（动态规划）

解法1：

1. 状态表示：

这道题可以根据「经验+题⽬要求」直接定义出状态表示：dp[i] 表示：到达i 位置时的最小花费。（注意：到达i 位置的时候， i 位置的钱不需要算上）。

2.状态转移方程

根据最近的⼀步，分情况讨论：

（1）先到达i - 1 的位置，然后⽀付cost[i - 1] ，接下来⾛⼀步⾛到i 位置： dp[i - 1] + csot[i - 1] 。

（2）先到达i - 2 的位置，然后⽀付cost[i - 2] ，接下来⾛⼀步⾛到i 位置： dp[i - 2] + csot[i - 2] 。

3.初始化

从我们的递推公式可以看出，我们需要先初始化i = 0 ，以及i = 1 位置的值。容易得到dp[0] = dp[1] = 0 ，因为不需要任何花费，就可以直接站在第0 层和第1 层上。

4.填表顺序

根据「状态转移方程」可得，遍历的顺序是「从左往右」。

5.返回值

根据「状态表⽰以及题目要求」，需要返回dp[n] 位置的值。

代码：

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        int n = cost.length;
        int[] dp = new int[n + 1];
        dp[0] = 0;dp[1] = 0;
        for(int i = 2;i <=n;i++){
            dp[i] = Math.min((dp[i - 2] + cost[i - 2]),(dp[i - 1] + cost[i - 1]));
        }
        return dp[n];
    }
}

解法2：

解法一和解法二的区别就是状态表示不一样，这样再描述一个解法二是为了告诉大家解法不一定只有一种选定状态表示去试一下状态转移方程（不要怕错）。

1. 状态表示：

dp[i] 表示：从i 位置出发，到达楼顶，此时的最小花费。

2.状态转移方程：

根据最近的⼀步，分情况讨论：

（1）支付cost[i] ，往后走⼀步，接下来从i + 1 的位置出发到终点： dp[i + 1] + cost[i] ；

（2）支付cost[i] ，往后走⼀步，接下来从i + 1 的位置出发到终点： dp[i + 1] + cost[i] ；

我们要的是最小花费，因此dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。

剩下三步我就不多赘述。

代码如下：

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        int n = cost.length;
        int[] dp = new int[n];
        dp[n - 1] = cost[n- 1];dp[n - 2] = cost[n - 2];
        for(int i = n - 3;i >= 0;i--){
            dp[i] = cost[i] + Math.min(dp[i + 1],dp[i + 2]);
        }
        return Math.min(dp[0],dp[1]);

    }
}

题目：解码方法

解法（动态规划）

1. 状态表示：

根据以往的经验，对于⼤多数线性dp ，我们经验上都是「以某个位置结束或者开始」做文章，这⾥我们继续尝试「⽤i位置为结尾」结合「题⽬要求」来定义状态表⽰。dp[i] 表⽰：字符串中[0，i] 区间上，⼀共有多少种编码⽅法。

2.状态转移方程

关于i 位置的编码状况，我们可以分为下⾯两种情况：

（1）让i 位置上的数单独解码成⼀个字⺟。

（2）让i 位置上的数与i - 1 位置上的数结合，解码成⼀个字⺟。

让i位置上的数单独解码成⼀个字⺟，就存在「解码成功」和「解码失败」两种情况：

（1）当i位置上的数单独解码成⼀个字⺟。

解码成功：当i 位置上的数在[1, 9] 之间的时候，说明i 位置上的数是可以单独解码的，那么此时[0, i] 区间上的解码⽅法应该等于[0, i - 1] 区间上的解码方法。因为[0, i - 1] 区间上的所有解码结果，后⾯填上⼀个i 位置解码后的字⺟就可以了。此时dp[i] = dp[i - 1] ；

解码失败：当i 位置上的数是0 的时候，说明i 位置上的数是不能单独解码的，那么此时[0, i] 区间上不存在解码⽅法。因为i 位置如果单独参与解码，但是解码失败了，那么前⾯做的努⼒就全部⽩费了。此时dp[i] = 0 。

（2）让i 位置上的数与i - 1 位置上的数结合，解码成⼀个字⺟。

解码成功：当结合的数在[10, 26] 之间的时候，说明[i - 1, i] 两个位置是可以解码成功的，那么此时[0, i] 区间上的解码⽅法应该等于[0, i - 2 ]区间上的解码⽅法，原因同上。此时dp[i] = dp[i - 2] ；

解码失败：当结合的数在[0, 9] 和[27 , 99] 之间的时候，说明两个位置结合后解码失败（这⾥⼀定要注意00 01 02 03 04 ......这⼏种情况），那么此时[0, i] 区间上的解码⽅法就不存在了，原因依旧同上。此时dp[i] = 0 。

综上所述： dp[i] 最终的结果应该是上⾯四种情况下，解码成功的两种的累加和（因为我们关⼼的是解码⽅法，既然解码失败，就不⽤加⼊到最终结果中去），因此可以得到状态转移⽅程（ dp[i] 默认初始化为0 ）：

（1）当s[i] 上的数在[1, 9] 区间上时： dp[i] += dp[i - 1] ；

（2）当s[i - 1] 与s[i] 上的数结合后，在[10, 26] 之间的时候： dp[i] += dp[i - 2] ；

如果上述两个判断都不成⽴，说明没有解码⽅法， dp[i] 就是默认值0 。

3.初始化

（1）当s[0] != '0' 时，能编码成功， dp[0] = 1 初始化dp[1] ：

（2）当s[1] 在[1，9] 之间时，能单独编码，此时dp[1] += dp[0] （原因同上， dp[1] 默认为0 ）

（3）当s[0] 与s[1] 结合后的数在[10, 26] 之间时，说明在前两个字符中，⼜有⼀种编码⽅式，此时dp[1] += 1 。

4.填表顺序

毫⽆疑问是「从左往右」

5.返回值

应该返回dp[n - 1] 的值，表⽰在[0, n - 1] 区间上的编码⽅法。

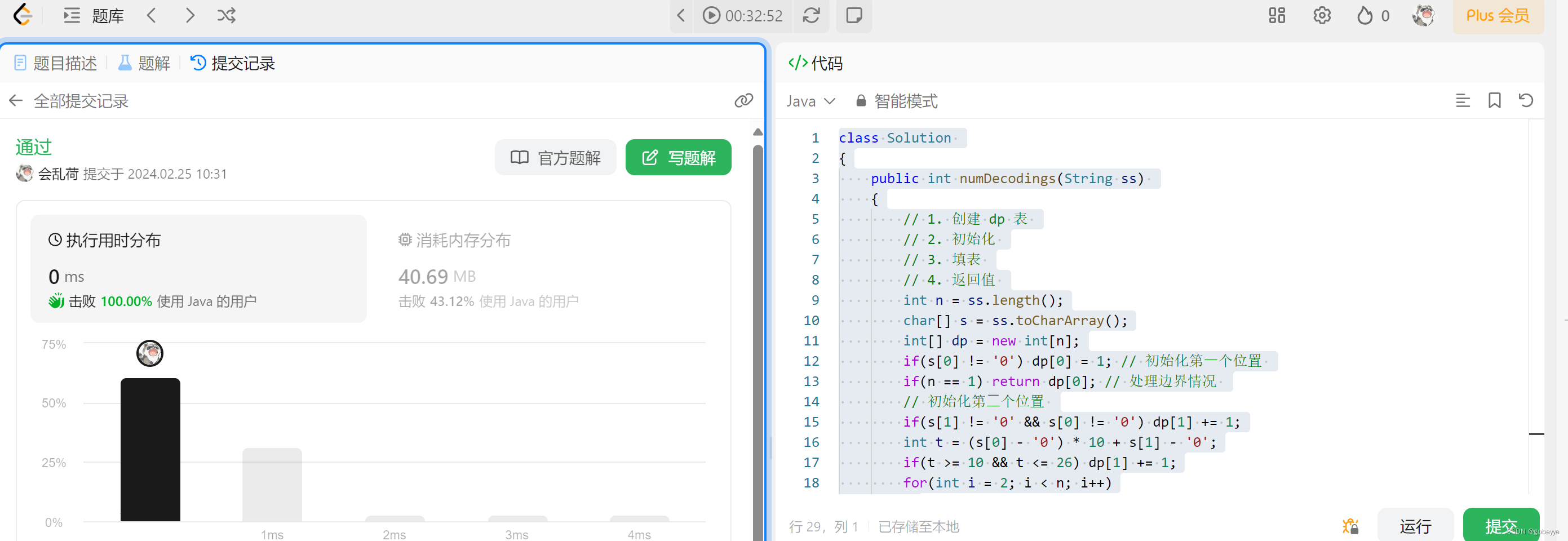
代码：

class Solution 
{
    public int numDecodings(String ss) 
    {
        // 1. 创建 dp 表 
        // 2. 初始化 
        // 3. 填表 
        // 4. 返回值 
        int n = ss.length();
        char[] s = ss.toCharArray();
        int[] dp = new int[n];
        if(s[0] != '0') dp[0] = 1; // 初始化第⼀个位置 
        if(n == 1) return dp[0]; // 处理边界情况 
        // 初始化第⼆个位置 
        if(s[1] != '0' && s[0] != '0') dp[1] += 1;
        int t = (s[0] - '0') * 10 + s[1] - '0';
        if(t >= 10 && t <= 26) dp[1] += 1;
        for(int i = 2; i < n; i++)
        {
         // 先处理第⼀种情况 
            if(s[i] != '0') dp[i] += dp[i - 1];
         // 处理第⼆种情况 
            int tt = (s[i - 1] - '0') * 10 + s[i] - '0';
            if(tt >= 10 && tt <= 26) dp[i] += dp[i - 2];
        }
        return dp[n - 1];
    }
}

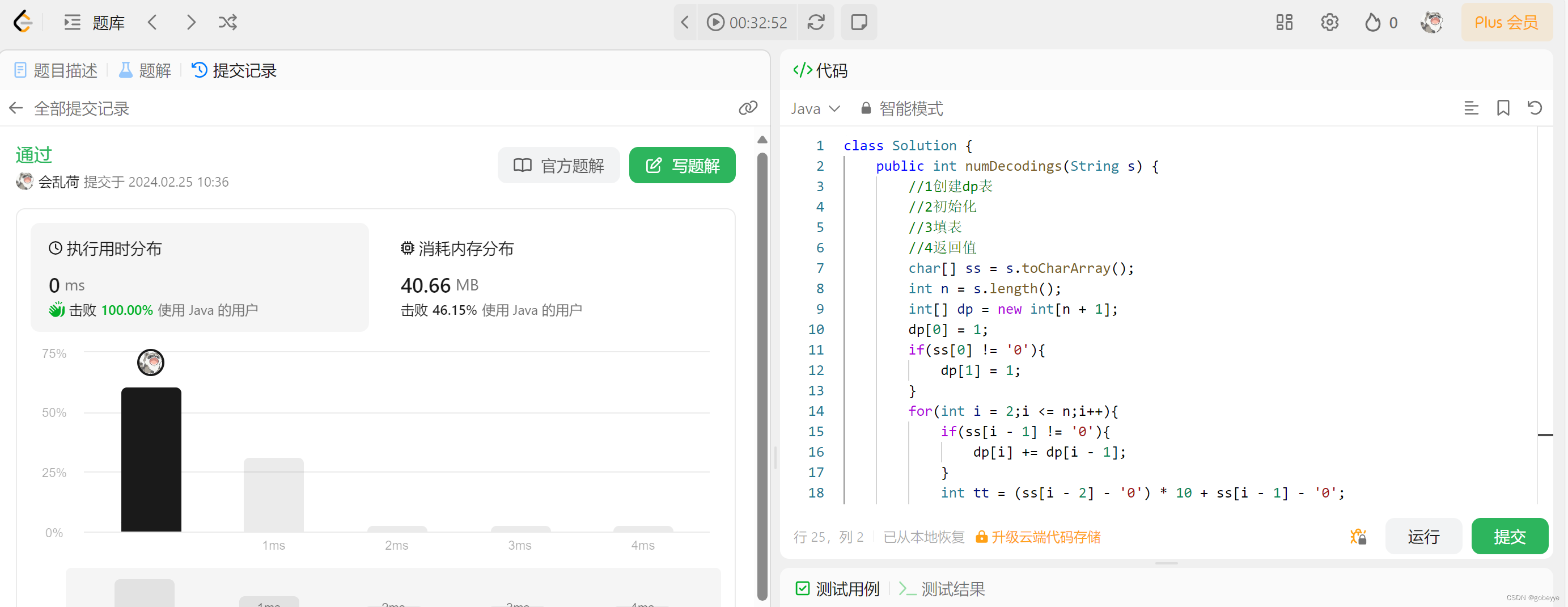
优化：

添加辅助位置初始化

可以在最前⾯加上⼀个辅助结点，帮助我们初始化。使⽤这种技巧要注意两个点：

（1）辅助结点⾥⾯的值要保证后续填表是正确的；

（2）下标的映射关系

使用这种方式可以减少初始化的负担dp[1]就可以不用初始化，且不用考虑边界问题，因为我们的dp数组会开辟n+1，里面原本的数据都向后移动一位，dp[0]一般是0或者1（具体看题）。

代码如下:

class Solution {
    public int numDecodings(String s) {
        //1创建dp表
        //2初始化
        //3填表
        //4返回值
        char[] ss = s.toCharArray();
        int n = s.length();
        int[] dp = new int[n + 1];
        dp[0] = 1;
        if(ss[0] != '0'){
            dp[1] = 1;
        }
        for(int i = 2;i <= n;i++){
            if(ss[i - 1] != '0'){
                dp[i] += dp[i - 1];
            }
            int tt = (ss[i - 2] - '0') * 10 + ss[i - 1] - '0';
            if(tt >= 10 && tt <= 26){
                dp[i] += dp[i - 2];
            }
        }
        return dp[n];
    }
}