什么是动态规划
动态规划简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点一定要和贪心区别出来,贪心没有状态推导,而是直接从局部直接选择最优。
在贪心中,有一个例子是背包问题。
eg:由N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能使用一次,求解将哪些物品装进背包里物品价值总和最大。
动态规划中dp[j]是由dp[j-weight]推导出的,然后取max(dp[j],dp[j-weight[i]+value[i])。
但如果是使用贪心,每次拿物品只会选择一个最大的或者最小的,和之前的状态没有什么关系。所以贪心解决不了动态规划的问题。
大家只需要明白动态规划是由前一个状态推导出来的,而贪心是局部直接选出最优的。
动态规划的解题步骤
做动态规划的题目的时候,很多同学包括我自己都有一个误区,就算将状态转移公式背下,然后照葫芦画瓢,然后根据公式进行代码书写,无论题目是否通过,都不清楚我们使用的dp[i]到底有什么用。
状态转移公式(递推公式)是很重要,但是仔细了解过后,或发现,动态规划不仅仅由递推公式。
对于动态规划,将其拆分为以下五部曲,这五步都搞懂,就基本可以把动态规划掌握:
1.确定dp数组以及其小标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
*一定不要忽略初始化,因为一些情况是递推公式决定了dp数组要如何初始化
动态规划应该如何debug
绝大部分同学,对于动态规划的题目是,看题解感觉会了,然后照葫芦画瓢,如果能过那就没关系,但是如果没过,那么怎么改都过不去,对于之前说的dp数组的初始化,递推公式,遍历顺序,都是处于一种什么都不明白的的状态。
找到问题的最好办法就是将dp数组打印出来,看看究竟是不是按照自己的思路推导的
做动态规划的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,最后确定推出的是否是想要的结果。
然后再写代码,如果代码没有通过,那就打印dp数组,看看是不是自己预先推导的哪里有出入。
如果打印出和自己预先模拟推导的一样,那么就算自己的递归公式、初始化或者遍历顺序有问题。如何还是不一样,那就是代码实现的细节有问题了。
这才是一个完整的思考过程,而不是代码出现了问题,就毫无头绪的乱改,最后依旧过不了,或者是稀里糊涂的过
从现在开始,写动态规划的题目出现问题或者无法通过,自己可以先思考这三个问题:
1.这道题我距离推导状态公式了吗
2.我们打印dp数组了吗
3.打印出的dp数组和我想的一样吗
如果这三个问题实现了,那么基本上动态规划的题目也就是解决了
亦或者是可以更清晰的明白自己究竟是哪一点不明白,是状态转移不明白,还是具体代码不知道该怎么写,还是不理解遍历dp数组的顺序。这样带着目的性的问题,就很好了。
LeetCode509.斐波那契数
题目描述:
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
解题思路:
·这道题大家再熟悉不过了,但是就是因为这题比较简单,所以大家可能并没有做什么分析,就顺手写过了,我们使用动态规划五部曲进行分析
1.确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2.确定递推公式
因为题目已经把递推公式给我们了,所以可以直接使用 dp[i] = dp[i-1] + dp[i-2]
3.dp数组如何初始化
题目中给的也很明确了
dp[0] = 0;dp[1] = 1;
4.确定遍历顺序,从递归公式中我们可以看出dp[i]是依赖dp[i-1]和dp[i-2],那么遍历顺序,就算一定是从前到后遍历
5.举例推导dp数组
按照递推公式,我们推导一下,当n为10时,数列应该是:0 1 1 2 3 5 8 13 21 34 55
如果最终代码无法通过,我们就将dp数组打印出,观察与我们推导的数列是不是一致的
以上,使用动态规划的方法全部分析完毕,代码如下:
class Solution {
public:
int fib(int n) {
if(n <= 1) return n;
vector<int> dp(n+1);
dp[0] = 0;
dp[1] = 1;
for(int i = 2;i <= n;i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
};·时间复杂度:O(n)
·空间复杂度:O(n)
总结:这道题虽然说非常的基础,但是我们严格按照动态规划五部曲进行分析,发现其实分析过程也并不会复杂,我们使用简单题目用于掌握方法,接下来的方法会越来越重要。
LeetCode70.爬楼梯
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
解题思路:
·这题仔细分析,多举几个例子,就会发现其规律。爬一层楼梯有一种方法,爬两层楼梯有两种方法,爬三层楼梯就可以根据前两层的规律进行推导
我们来进行动态规划五部曲的分析:
1.确定dp数组以及下标的含义
dp[i]:爬到第i层楼梯,有dp[i]种方法
2.确定递推公式
这道题怎么样才能推导出dp[i]呢?
从dp[i]的定义可以看出,dp[i]可以有两个方向可以推导出
首先是dp[i-1],上i-1层楼梯,有dp[i-1]种方法,那么再一步跳一个台阶不就是dp[i]了
dp[i-2]也是一样的思想,有dp[i-2]种方法,那么再一步跳两个个台阶不就是dp[i]了
所以就可以得出结论 dp[i]就算dp[i-1]和dp[i-2]之和
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,这就体现出确定dp数组以及下标的含义的重要性
3.dp数组如何初始化
dp[0] = 1,因为不动也是一种移动方法
dp[1] = 1,只有一步可以走
dp[2] = 2 ,有一步和两步可以走,所以我们就可以从i=3开始递推
4.确定遍历顺序
从递推公式dp[i] = dp[i-1]+dp[i-2]可以看出,遍历顺序一定是从前向后的
5.举例推导dp数组
我们会发现这个数组推导出来就算斐波那契,如果代码出现问题,那么就把dp数组打印出来,看看是否和自己推导的一样
代码如下:
class Solution {
public:
int climbStairs(int n) {
if(n <= 1) return n;
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i <= n;i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
};时间复杂度:O(n)
空间复杂度:O(n)
总结:这道题其实和斐波那契数题目是一样的,但是动态规划五部曲,却比上一题复杂了那么多
关键就算斐波那契题目描述中,已经把递归公式和如何初始化都给出来了,剩下的就很好推出
但是本题需要逐个分析,大家应该初步感受出了动态规划的五部曲了
LeetCode746.使用最小花费爬楼梯
题目描述:
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
解题思路:
1.确定dp数组以及下标的含义
使用动态规划,需要使用一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了
dp[i]的定义:达到第i个台阶所花费的最少体力为dp[i]
2.对于递推公式
得到dp[i],需要知道dp[i-1]和dp[i-2]
而dp[i-1]跳到dp[i]需要花费dp[i-1]+cost[i-1]
dp[i-2]跳到dp[i]需要花费dp[i-2]+dp[i-2]
按照题目要求,所以我们选择最小的,dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3.dp数组如何初始化
看了递推公式,所以我们就可以知道需要初始化dp[i-1]和dp[i-2],也就是dp[0]dp[1]
题目中说可以选择下标为0或下标为1的台阶开始爬楼梯,也就是说到达第0个台阶和第一个台阶是不花费的,所以dp[0] = dp[1] = 0
4.确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]和dp[i-2]推出,所以是从前到后遍历cost数组即可\
5.举例推导dp数组
我们使用示例2进行举例
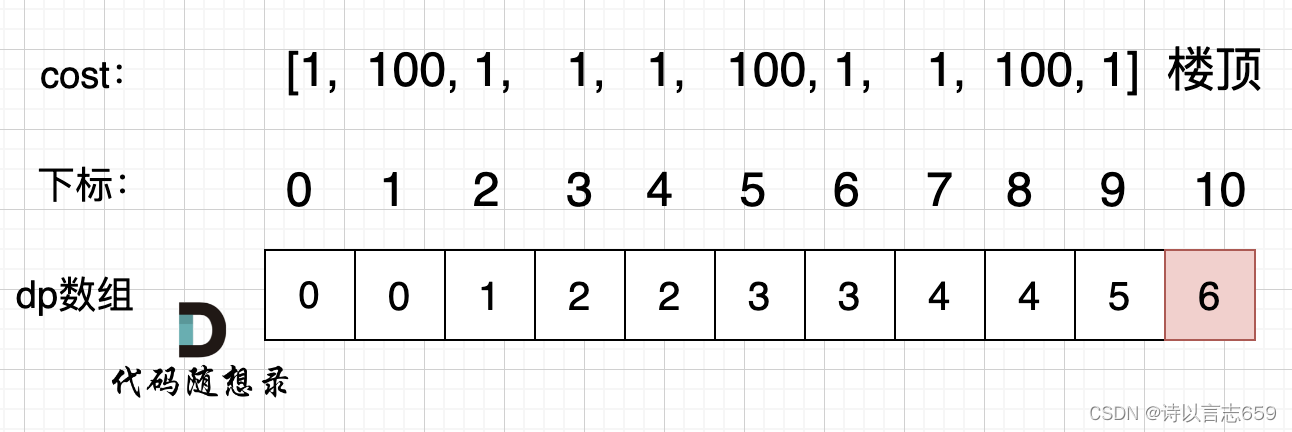
如果代码出现问题,就将dp数组打印出来,看看和如上推导是不是一样的
代码如下:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size()+1);
dp[0] = 0;
dp[1] = 0;
for(int i = 2;i <= cost.size();i++){
dp[i] = min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]);
}
return dp[cost.size()];
}
};·时间复杂度:O(n)
·空间复杂度:O(n)
总结:这题和爬楼梯也是类似,只是多了一个需要花费的部分,所以并没有什么难理解的地方







![[electron]官方示例解析](https://img-blog.csdnimg.cn/direct/fdd74d254f754b21964f63e454af6ebb.png)