pclpy 半径最近邻搜索
- 一、算法原理
- 1.KD-Tree 介绍
- 2.原理
- 二、代码
- 三、结果
- 1.原点云
- 2.半径最近邻搜索的点云
- 四、相关数据
一、算法原理
1.KD-Tree 介绍
kd 树或 k 维树是计算机科学中使用的一种数据结构,用于在具有 k 维的空间中组织一定数量的点。它是一个二叉搜索树,对其施加了其他约束。Kd 树对于范围和最近邻搜索非常有用。出于我们的目的,我们通常只会处理三维的点云,因此我们所有的 kd 树都是三维的。kd 树的每一层使用垂直于相应轴的超平面沿特定维度拆分所有子节点。在树的根部,所有子节点都将根据第一维进行拆分(即,如果第一维坐标小于根,它将在左子树中,如果大于根,则显然将在左子树中右子树)。树中的每一层都在下一个维度上进行划分,一旦所有其他维度都用尽,则返回到第一个维度。构建 kd 树的最有效方法是使用像 Quick Sort 那样的分区方法,将中点放在根处,将一维值较小的所有内容放在左侧,右侧较大。然后在左子树和右子树上重复此过程,直到要分区的最后一棵树仅由一个元素组成。
来自[维基百科]:
这是一个二维 KD-Tree的例子
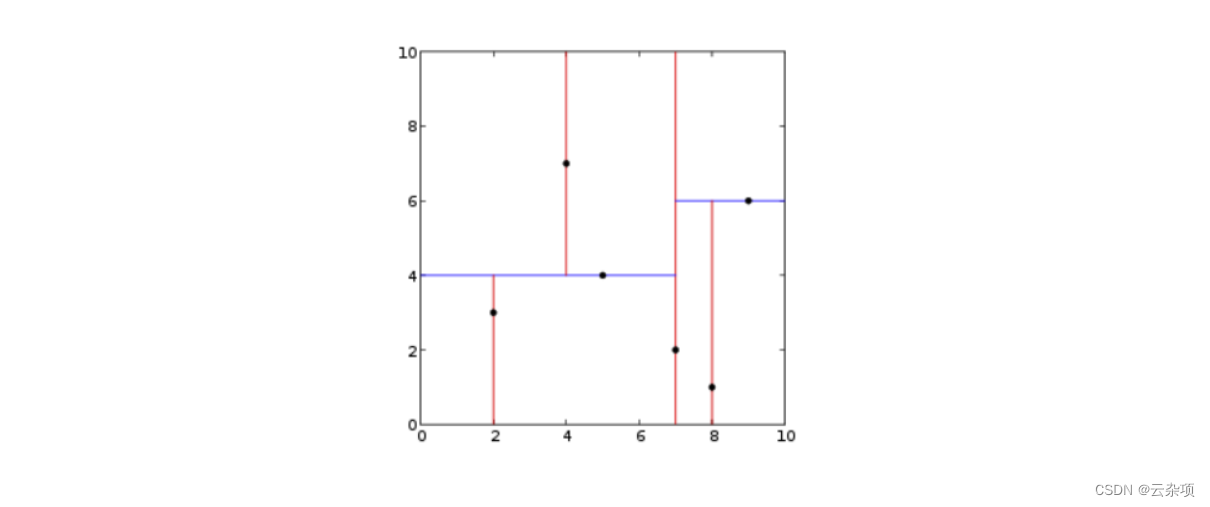
2.原理
- KD-Tree构建: 首先,选择一个数据集中的点作为根节点,并根据这个点的一个坐标轴(通常是数据维度中的一个)将数据集分成两个子集。然后,对每个子集递归地应用相同的过程,选择该子集中的一个点作为子树的根节点,并使用另一个坐标轴来分割子集。这个过程一直持续下去,直到每个子集的大小达到某个阈值,或者直到无法再分割为止。
- 节点分割: 在每一层中,
kd-Tree选择一个坐标轴,然后根据该坐标轴上的中位数将数据集分成两半。这个过程使得树的每个节点都代表一个超矩形区域,其中包含了数据集的部分或全部点。 - **最近半径搜索:**对于每个指定的查询点,搜索其半径范围内的所有邻居点。
二、代码
from pclpy import pcl
if __name__ == '__main__':
# 读取点云数据
cloud = pcl.PointCloud.PointXYZ()
reader = pcl.io.PCDReader()
reader.read("res/bunny.pcd", cloud)
# 构建kd-tree
kdtree = pcl.kdtree.KdTreeFLANN.PointXYZ()
kdtree.setInputCloud(cloud)
# 设置一个点云点
searchPoint = pcl.point_types.PointXYZ()
searchPoint.x = cloud.xyz[0][0] # x
searchPoint.y = cloud.xyz[0][1] # y
searchPoint.z = cloud.xyz[0][2] # z
print(searchPoint)
# # ------------ 使用半径最近邻搜索 -------------
# 创建了2个向量来存储有关我们邻居的信息
pointIdxRadiusSearch = pcl.vectors.Int()
pointRadiusSquaredDistance = pcl.vectors.Float()
# 设置搜索半径
radius = 0.01
print("索引点 (", searchPoint.x,
" ", searchPoint.y, " ", searchPoint.z, ") 半径=",
radius)
if kdtree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0:
for i in range(len(pointIdxRadiusSearch)):
print(" ", cloud.x[pointIdxRadiusSearch[i]],
" ", cloud.y[pointIdxRadiusSearch[i]],
" ", cloud.z[pointIdxRadiusSearch[i]],
" (平方距离: ", pointRadiusSquaredDistance[i], ")")
# # 将搜索的点保存
searchPointArray = cloud.xyz[pointIdxRadiusSearch]
searchCloud = pcl.PointCloud.PointXYZ.from_array(searchPointArray)
viewer = pcl.visualization.PCLVisualizer("3D viewer") # 建立一个可视化对象,窗口名 3D viewer
viewer.addPointCloud(searchCloud) # 点云数据添加到可刷对象中
while not viewer.wasStopped(): # 展示可视化对象
viewer.spinOnce(10)
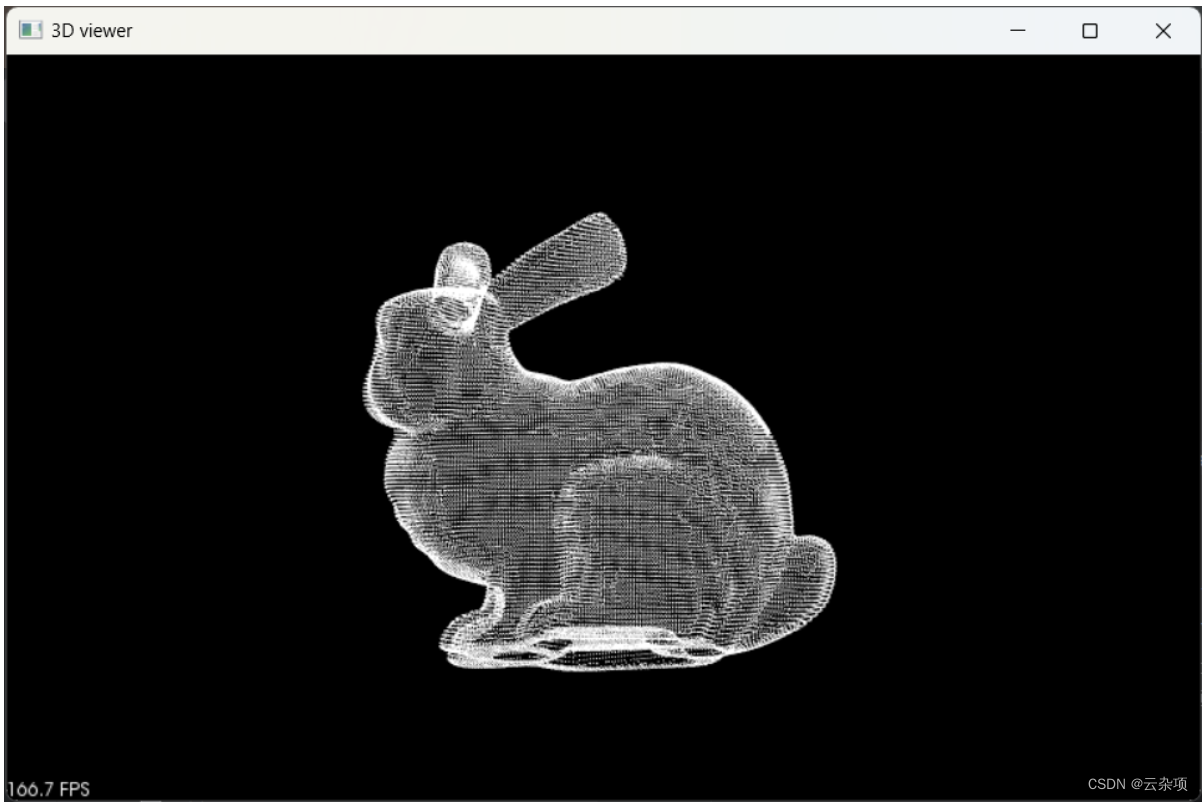
三、结果
1.原点云
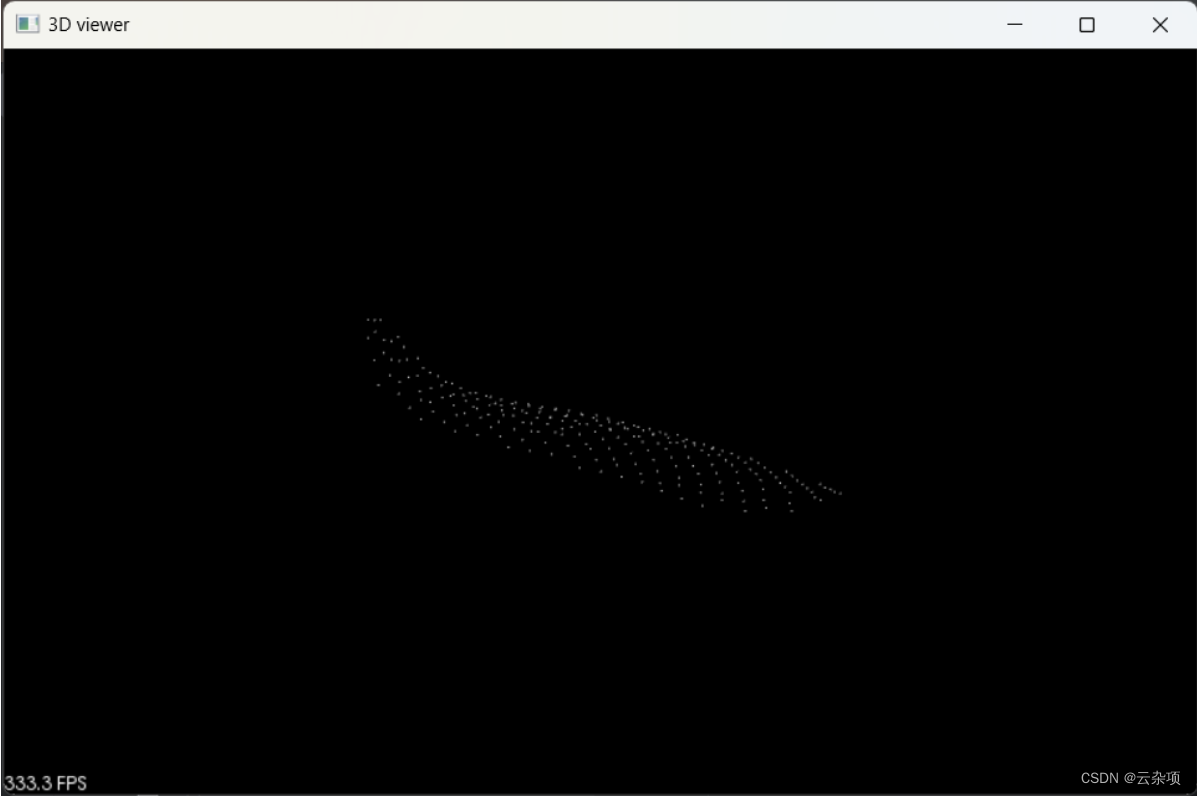
2.半径最近邻搜索的点云
四、相关数据
open3d和numpy计算半径邻搜索:https://blog.csdn.net/m0_73126623/article/details/136124928
测试数据下载链接:https://pan.baidu.com/s/1uT6UbzU5h7wPurnQYUB7TQ
提取码:lsyg







![sql注入 [极客大挑战 2019]FinalSQL1](https://img-blog.csdnimg.cn/direct/b7855373678e4af5a06421440a1183b7.png)


