前言

安卓SparseArray中多次用到了ContainerHelpers的binarySearch方法，其中的核心在于>>>:无符号右移位运算符,所以首先了解一下>>>无符号右移运算位

---

一、JAVA移位运算符

1.1 >> 带符号右移位运算符

在 Java 中，>> 是带符号右移位运算符，用于将一个数的二进制表示向右移动指定的位数，并在左侧用原来的符号位填充。>> 的工作原理如下：

1. 对于正数：

• 右移操作会将二进制数向右移动指定的位数，高位用 0 填充。
• 例如，对于 5 >> 1，二进制表示为 00000101，右移 1 位后变为 00000010，即十进制为 2。

2. 对于负数：

• 如果是负数，右移操作会保留符号位，即最高位的符号位（1 表示负数，0 表示正数）会在移位过程中保持不变。
  例如，对于 -5 >> 1，二进制表示为 11111011（-5 的补码形式），右移 1 位后变为 11111101，即十进制为 -3。

3. 注意事项：

• 右移操作会丢弃被移出的位，所以右移可能导致数据丢失。
• 右移一位相当于除以 2 的整数部分，右移 n 位相当于除以 2 的 n 次方的整数部分。
• 对于负数的右移操作，可能会导致结果不同于直接除以 2 的整数部分，因为符号位的影响。

>> 是 Java 中的带符号右移位运算符，用于将二进制数向右移动指定的位数，保留符号位并用原符号位填充。这个操作在处理二进制数时非常有用，可以实现快速的位运算操作。

1.2 >>> 无符号右移位运算符

在 Java 中，>>> 是无符号右移位运算符，用于将一个数的二进制表示向右移动指定的位数，高位用 0 填充。相比之下，>> 是有符号右移位运算符，高位用原符号位填充。 >>> 的用法和特点：

>>>的使用：
>>> 是 Java 中的无符号右移位运算符，用于将一个数的二进制表示向右移动指定的位数，高位用 0 填充。
例如，5 >>> 1，二进制表示为 00000101，右移 1 位后变为 0000 0010，即十进制为 2。
例如，-5 >>> 1 ，二进制表示为 11111011，右移 1 位后变为 0111 1101，即十进制为 125。
无符号右移的特点：
无符号右移操作会将二进制数向右移动指定的位数，高位用 0 填充。
无符号右移操作可以用于处理无符号数，避免有符号右移可能导致的符号位扩展问题。
对于负数的无符号右移操作，仍然会将二进制数向右移动，高位用 0 填充，不会受到符号位的影响。

>>> 是 Java 中的无符号右移位运算符，用于将一个数的二进制表示向右移动指定的位数，并在高位用 0 填充。与有符号右移位运算符 >> 相比，无符号右移操作不受符号位的影响，适用于处理无符号数。

1.3 << 左移位运算符

在 Java 中，<< 是左移位运算符，用于将一个数的二进制表示向左移动指定的位数，并在右侧用 0 填充。

左移位运算符 <<：
对于正数：
左移操作会将二进制数向左移动指定的位数，低位用 0 填充。
例如，对于 5 << 1，二进制表示为 00000101，左移 1 位后变为 00001010，即十进制为 10。
对于负数：
左移操作同样会将二进制数向左移动指定的位数，低位用 0 填充。
例如，对于 -5 << 1，二进制表示为 11111011（-5 的补码形式），左移 1 位后变为 11110110，即十进制为 -10。
注意事项：
左移操作会在右侧用 0 填充，所以左移可能导致高位溢出。
左移一位相当于乘以 2，左移 n 位相当于乘以 2 的 n 次方。
对于负数的左移操作，可能会导致结果不同于直接乘以 2，因为补码的符号位的影响。

<< 是 Java 中的左移位运算符，用于将一个数的二进制表示向左移动指定的位数，并在右侧用 0 填充。左移操作可以实现快速的位运算操作，对于乘以 2 的整数倍的操作特别有用。

1.4 Java 中没有 <<<

1.5 ~取反操作

当n为正数时，~(n) = -(n+1)  ~(2)=-3

当n为负数时，~(-n) = n - 1，忽略负号。 ~(-3)=2

二、ContainerHelpers二分查找算法

有了上面的基础我们可以更快的分析ContainerHelpers的二分查找算法

ContainerHelpers.java源码如下：

package android.util;

class ContainerHelpers {

    // This is Arrays.binarySearch(), but doesn't do any argument validation.
    static int binarySearch(int[] array, int size, int value) {
        int lo = 0;
        int hi = size - 1;

        while (lo <= hi) {
            final int mid = (lo + hi) >>> 1;
            final int midVal = array[mid];

            if (midVal < value) {
                lo = mid + 1;
            } else if (midVal > value) {
                hi = mid - 1;
            } else {
                return mid;  // value found
            }
        }
        return ~lo;  // value not present
    }

    static int binarySearch(long[] array, int size, long value) {
        int lo = 0;
        int hi = size - 1;

        while (lo <= hi) {
            final int mid = (lo + hi) >>> 1;
            final long midVal = array[mid];

            if (midVal < value) {
                lo = mid + 1;
            } else if (midVal > value) {
                hi = mid - 1;
            } else {
                return mid;  // value found
            }
        }
        return ~lo;  // value not present
    }
}

这段代码是一个经典的二分查找算法实现，用于在一个已排序的数组中查找给定的值。

static int binarySearch(int[] array, int size, int value)：
这是一个静态方法，接受一个 int 类型的数组 array、数组的大小 size 和要查找的值 value 作为参数。
方法返回要查找的值在数组中的索引位置，如果值不存在，则返回一个负数，表示值应该插入的位置。
初始化和循环：
int lo = 0;
int hi = size - 1;
while (lo <= hi) {
首先，初始化两个int类型位置 lo 和 hi，分别指向数组的起始位置和结束位置。
进入一个 while 循环，条件是 lo <= hi，即当搜索范围不为空时继续搜索。
计算中间位置和中间值：
final int mid = (lo + hi) >>> 1;
final long midVal = array[mid];
在每次循环中，计算中间位置 mid，这里使用了无符号右移位运算符 >>> 替换 /2来避免溢出。
获取中间位置对应的值 midVal，即数组中间位置的元素值。
比较中间值和目标值：
if (midVal < value) {
lo = mid + 1;
} else if (midVal > value) {
hi = mid - 1;
} else {
return mid; // value found
}
如果 midVal 小于目标值 value，则更新 lo 为 mid + 1，缩小搜索范围到右半部分。
如果 midVal 大于目标值 value，则更新 hi 为 mid - 1，缩小搜索范围到左半部分。
如果 midVal 等于目标值 value，则直接返回 mid，表示找到了目标值的索引位置。
结果返回：
return ~lo; // value not present
如果循环结束时仍未找到目标值，说明值不存在于数组中，此时返回 ~lo。

二分查找法中为什么使用>>>1 而不是/2呢?

在二分查找算法中，我们需要找到数组的中间位置来比较中间值和目标值，以确定搜索范围的缩小方向。在这里使用无符号右移位运算符 >>> 来计算中间位置的原因是为了避免溢出，并且确保取到的是中间位置。
在计算中间位置时，我们通常使用 (lo + hi) / 2 来获取中间位置，但是这种方式可能存在溢出的风险，尤其是当 lo 和 hi 非常大时。为了避免这种情况，我们可以使用无符号右移位运算符 >>>，它会将二进制数向右移动指定的位数，高位补0。
具体来说，假设 lo 和 hi 都是正整数，无符号右移位运算符 >>> 可以确保取到的中间位置是两者之和的一半，即 (lo + hi) / 2。这样就能够有效地计算中间位置，而且不会出现溢出的情况。
因此，使用无符号右移位运算符 >>> 来计算中间位置可以确保取到正确的中间值，同时避免溢出的问题，从而保证二分查找算法的正确性和效率。

如果数组中没有传入的value,那么返回值是多少呢？
示例：

假设有一个有序数组 array = {2, 4, 6, 8, 10}，我们要在这个数组中查找值为 5 的元素。我们使用给定的二分查找算法进行查找，以下是具体的步骤和结果：

1. 初始时，lo = 0，hi = 4，数组大小为 size = 5。
2. 第一次循环迭代：

• 计算中间索引 mid = (0 + 4) >>> 1 = 2，即中间元素为 6。
• 由于 6 > 5，所以更新 hi = 2 - 1 = 1。

3. 第二次循环迭代：
   - 计算中间索引 mid = (0 + 1) >>> 1 = 0，即中间元素为 2。
   - 由于 2 < 5，所以更新 lo = 0 + 1 = 1。
4. 第三次循环迭代：
   - 此时 lo = 1，hi = 1，计算中间索引 mid = (1 + 1) >>> 1 = 1，即中间元素为 4。
   - 由于 4 < 5，所以更新 lo = 1 + 1 = 2。
5. 循环结束，此时 lo = 2，hi = 1。因为 lo > hi，表示整个数组已经被搜索完毕，但没有找到目标值 5。
6. 最终返回 ~lo，即取反 2 的结果为 -3。

如果索引值为3的话，那岂不是要插入到6-8之间了
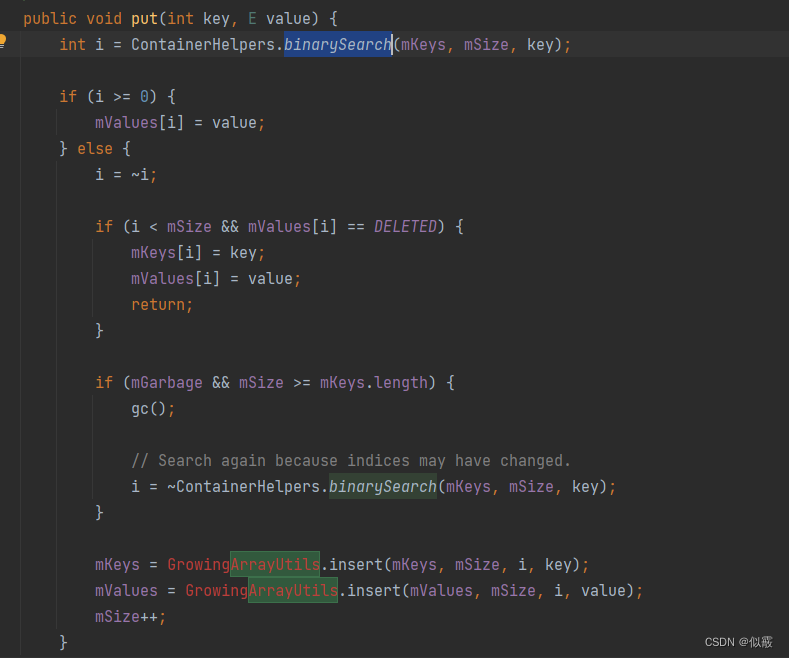
看一下SparseArray的put方法：
如果是负值，还会再取反回来再按照索引2去插入的,即插入到4-6之间。

---

总结

ContainerHelpers这段代码实现了一个二分查找算法，通过不断缩小搜索范围来查找目标值在已排序数组中的位置。如果值存在，则返回其索引位置；如果值不存在，则返回应该插入的位置。这是一个高效的查找算法，时间复杂度为 O(log n)，适用于已排序的数组。