---

---

权重初始化方法

Xavier初始化（Xavier initialization）

是一种用于初始化神经网络权重的方法，也称为Glorot初始化。更有效地传播信号并减少梯度消失或梯度爆炸的问题。适用于激活函数为tanh或sigmoid的情况。

Xavier初始化的计算方法如下：

1. Glorot（或 Xavier）初始化：
   • 适用于激活函数如sigmoid和tanh。
   • 初始化公式：$\sigma =\sqrt{\frac{2}{n_{\text{in}}+n_{\text{out}}}}$
     其中，$n_{\text{in}}$ 是输入单元数，$n_{\text{out}}$ 是输出单元数。

对于单个神经元的权重w，从均匀分布或正态分布中随机采样，具体取决于所选择的激活函数：

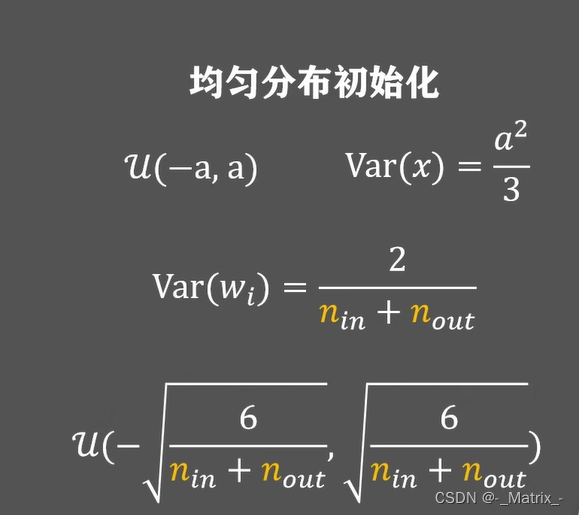
1. 如果使用tanh激活函数，从均匀分布采样：
   • 采样范围：[-sqrt(6 / (n_in + n_out)), sqrt(6 / (n_in + n_out))]
   • 其中n_in是上一层的输入节点数量，n_out是当前层的输出节点数量。

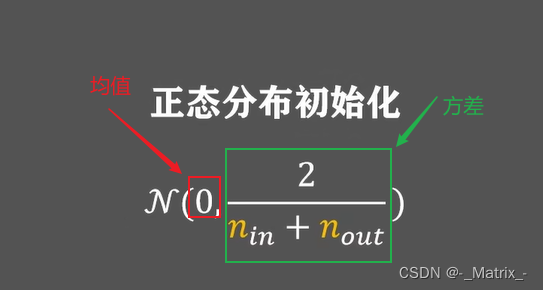
2. 如果使用sigmoid激活函数，从正态分布采样：
   • 均值：0
   • 方差：sqrt(2 / (n_in + n_out))
   • 其中n_in是上一层的输入节点数量，n_out是当前层的输出节点数量。

Kaiming初始化，也称为He初始化

2. He 初始化：
   • 适用于ReLU及其变种（如LeakyReLU）激活函数。
   • 初始化公式：$\sigma =\sqrt{\frac{2}{n_{\text{in}}}}$

这种初始化方法主要用于修正线性单元（Rectified Linear Units，ReLU）激活函数的神经网络。

与Xavier初始化适用于tanh和sigmoid等S型激活函数不同，Kaiming初始化专门针对ReLU激活函数的特性进行优化。ReLU是一个常用的非线性激活函数，它在输入大于零时保持不变，在输入小于等于零时输出为零。

Kaiming初始化的计算方法如下：

对于单个神经元的权重w，从均匀分布或正态分布中随机采样，具体取决于所选择的激活函数：

1. 如果使用ReLU激活函数，从正态分布采样：

   • 均值：0
   • 方差：sqrt(2 / n_in)
   • 其中n_in是上一层的输入节点数量。

2. 对于带有ReLU激活的卷积层，可以使用相同的初始化方法，只是需要考虑卷积层的输入通道数量（即n_in）。

LeCun 初始化

• 适用于Sigmoid激活函数。
• 初始化公式：$\sigma =\sqrt{\frac{1}{n_{\text{in}}}}$

正态分布与均匀分布

• 使用较小的标准差（如0.01）从正态分布中采样权重。
• 使用较小的范围（如-0.01到0.01）从均匀分布中采样权重。

Orthogonal Initialization

• 使用正交矩阵初始化权重。这种初始化方法对于某些任务和模型架构可能很有益。

Sparse Initialization

• 将大部分权重初始化为0，只初始化一小部分非零的权重。

n_in和n_out

n_in和n_out分别表示神经网络层的输入节点数量和输出节点数量。这些节点也称为神经元，它们是网络的基本组成部分。

• n_in：代表上一层（前一层）的节点数量，也就是当前层的输入数量。在神经网络中，每个神经元都会接收来自上一层所有节点的输入，这些输入被加权和后传递给当前神经元的激活函数。因此，n_in指的是上一层与当前层之间的连接数量。

• n_out：代表当前层的节点数量，也就是当前层的输出数量。每个神经元会将经过激活函数处理后的结果传递给下一层所有节点，形成下一层的输入。因此，n_out指的是当前层与下一层之间的连接数量。

代码实现

#include <iostream>
#include <Eigen/Dense>
#include <random>
#include <cmath>

Eigen::MatrixXd glorotInitialize(int rows, int cols);
Eigen::MatrixXd heInitialize(int rows, int cols);
Eigen::MatrixXd lecunInitialize(int rows, int cols);
Eigen::MatrixXd normalDistributionInitialize(int rows, int cols, double std_dev=0.01);
Eigen::MatrixXd uniformDistributionInitialize(int rows, int cols, double limit=0.01);
Eigen::MatrixXd orthogonalInitialize(int rows, int cols);
// Sparse Initialization需要额外参数来确定稀疏度，这里我们使用一个简化版本，指定一个非零的权重数。
Eigen::MatrixXd sparseInitialize(int rows, int cols, int nonZeroCount);



//1. **Glorot (Xavier) Initialization**:

Eigen::MatrixXd glorotInitialize(int rows, int cols) {
    std::random_device rd;
    std::mt19937 gen(rd());
    double limit = sqrt(6.0 / (rows + cols));
    std::uniform_real_distribution<> dis(-limit, limit);

    Eigen::MatrixXd matrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            matrix(i, j) = dis(gen);
        }
    }
    return matrix;
}


//**He Initialization**:

Eigen::MatrixXd heInitialize(int rows, int cols) {
    std::random_device rd;
    std::mt19937 gen(rd());
    double std_dev = sqrt(2.0 / rows);
    std::normal_distribution<> dis(0, std_dev);

    Eigen::MatrixXd matrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            matrix(i, j) = dis(gen);
        }
    }
    return matrix;
}


//3. **LeCun Initialization**:

Eigen::MatrixXd lecunInitialize(int rows, int cols) {
    std::random_device rd;
    std::mt19937 gen(rd());
    double std_dev = sqrt(1.0 / rows);
    std::normal_distribution<> dis(0, std_dev);

    Eigen::MatrixXd matrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            matrix(i, j) = dis(gen);
        }
    }
    return matrix;
}


//4. **Normal Distribution Initialization**:

Eigen::MatrixXd normalDistributionInitialize(int rows, int cols, double std_dev) {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::normal_distribution<> dis(0, std_dev);

    Eigen::MatrixXd matrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            matrix(i, j) = dis(gen);
        }
    }
    return matrix;
}

//5. **Uniform Distribution Initialization**:

Eigen::MatrixXd uniformDistributionInitialize(int rows, int cols, double limit) {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> dis(-limit, limit);

    Eigen::MatrixXd matrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            matrix(i, j) = dis(gen);
        }
    }
    return matrix;
}


//6. **Orthogonal Initialization**:
Eigen::MatrixXd orthogonalInitialize(int rows, int cols) {
    // 创建一个随机矩阵
    std::random_device rd;
    std::mt19937 gen(rd());
    std::normal_distribution<> dis(0, 1);

    Eigen::MatrixXd randomMatrix(rows, cols);
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            randomMatrix(i, j) = dis(gen);
        }
    }

    // 使用QR分解获得正交矩阵
    Eigen::HouseholderQR<Eigen::MatrixXd> qr(randomMatrix);
    Eigen::MatrixXd orthogonalMatrix = qr.householderQ();

    // 如果您需要一个具有特定维度的正交矩阵（例如rows != cols），您可以选择一个子矩阵
    return orthogonalMatrix.block(0, 0, rows, cols);
}


//7. **Sparse Initialization**:

Eigen::MatrixXd sparseInitialize(int rows, int cols, int nonZeroCount) {
    Eigen::MatrixXd matrix = Eigen::MatrixXd::Zero(rows, cols);
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> dis(-1, 1);

    for(int i = 0; i < nonZeroCount; i++) {
        int r = rand() % rows;
        int c = rand() % cols;
        matrix(r, c) = dis(gen);
    }

    return matrix;
}
int main() {
    int rows = 5;
    int cols = 5;

    // Glorot Initialization
    Eigen::MatrixXd weights_glorot = glorotInitialize(rows, cols);
    std::cout << "Glorot Initialized Weights:" << std::endl << weights_glorot << std::endl << std::endl;

    // He Initialization
    Eigen::MatrixXd weights_he = heInitialize(rows, cols);
    std::cout << "He Initialized Weights:" << std::endl << weights_he << std::endl << std::endl;

    // LeCun Initialization
    Eigen::MatrixXd weights_lecun = lecunInitialize(rows, cols);
    std::cout << "LeCun Initialized Weights:" << std::endl << weights_lecun << std::endl << std::endl;

    // Normal Distribution Initialization
    Eigen::MatrixXd weights_normal = normalDistributionInitialize(rows, cols);
    std::cout << "Normal Distribution Initialized Weights:" << std::endl << weights_normal << std::endl << std::endl;

    // Uniform Distribution Initialization
    Eigen::MatrixXd weights_uniform = uniformDistributionInitialize(rows, cols);
    std::cout << "Uniform Distribution Initialized Weights:" << std::endl << weights_uniform << std::endl << std::endl;

    // Sparse Initialization
    int nonZeroCount = 10; // As an example, set 10 weights to non-zero values
    Eigen::MatrixXd weights_sparse = sparseInitialize(rows, cols, nonZeroCount);
    std::cout << "Sparse Initialized Weights with " << nonZeroCount << " non-zero values:" << std::endl << weights_sparse << std::endl;

    return 0;
}