学习参考:
- 动手学深度学习2.0
- Deep-Learning-with-TensorFlow-book
- pytorchlightning
一、数组与张量
虽然张量看起来是复杂的对象,但它们可以理解为向量和矩阵的集合。理解向量和矩阵对于理解张量至关重要。
- 向量是元素的一维列表,向量是一个有序的数列,可以表示为一维数组。通常用来表示空间中的方向和大小。
- 矩阵是向量的二维列表,阵是一个二维数组,由行和列组成。通常用来表示线性变换、数据集合等。
- 张量可以被视为多维矩阵列表,张量是一个多维数组,可以看作是向量和矩阵的推广。在深度学习和机器学习中,张量是数据的基本表示形式。0阶张量是标量(Scalar)、1阶张量是向量、2阶张量是矩阵,以此类推。
TensorFlow中的Tensors是不可变的,也不能被赋值。 TensorFlow中的Variables是支持赋值的可变容器。 请记住,TensorFlow中的梯度不会通过Variable反向传播。
1.张量创建
张量表示一个由数值组成的数组,这个数组可能有多个维度]。 具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix); 具有两个轴以上的张量没有特殊的数学名称。
如何创建张量?
(1)range方法
import tensorflow as tf
x = tf.range(12)
#可以通过张量的shape属性来访问张量(沿每个轴的长度)的形状
print(x.shape)
# 如果只想知道张量中元素的总数,即形状的所有元素乘积,可以检查它的大小(size)。
print(tf.size(x))
使用全0、全1、其他常量,或者从特定分布中随机采样的数字]来初始化张量。
print(tf.ones((2, 3, 4)))
tf.zeros((2, 3, 4))
(2)从某个概率分布中采样创建
通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。 例如,当构造数组来作为神经网络中的参数时,通常会随机初始化参数的值。 以下代码创建一个形状为(3,4)的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
tf.random.normal(shape=[3, 4])
<tf.Tensor: shape=(3, 4), dtype=float32, numpy=
array([[ 0.77872986, -0.82767004, 1.489659 , 0.3403899 ],
[-0.07687712, -1.2800221 , 0.48299474, -0.5643912 ],
[-1.0667747 , 0.32837722, -0.02862396, -0.49701583]],
dtype=float32)>
(3)从其它数据结构(如列表)创建
通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值]
tf.constant([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
<tf.Tensor: shape=(3, 4), dtype=int32, numpy=
array([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])>
2.改变维度
要想改变一个张量的形状而不改变元素数量和元素值,可以调用reshape函数。
X = tf.reshape(x, (3, 4))
X
<tf.Tensor: shape=(3, 4), dtype=int32, numpy=
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])>
不需要通过手动指定每个维度来改变形状。 也就是说,如果的目标形状是(高度,宽度), 那么在知道宽度后,高度会被自动计算得出,不必自己做除法。 在上面的例子中,为了获得一个3行的矩阵,我们手动指定了它有3行和4列。 幸运的是,可以通过-1来调用此自动计算出维度的功能。 即可以用x.reshape(-1,4)或x.reshape(3,-1)来取代x.reshape(3,4)。
tf.reshape(x, (4, -1))
<tf.Tensor: shape=(4, 3), dtype=int32, numpy=
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])>
3.长度、维度和形状
调用Python的内置len()函数来访问张量的长度
x = tf.range(4)
len(x),len(tf.constant([[1,2,3,5,6],[1,2,3,9,6]]))
形状(shape)是一个元素组,列出了张量沿每个轴的长度(维数)。
x.shape
二、按元素运算(运算符)
在数据上执行数学运算,其中最简单且最有用的操作是按元素(elementwise)运算。 它们将标准标量运算符应用于数组的每个元素。 对于将两个数组作为输入的函数,按元素运算将二元运算符应用于两个数组中的每对位置对应的元素。 可以基于任何从标量到标量的函数来创建按元素函数。
1. 基本运算(按元素位置)
对于任意具有相同形状的张量, [常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算]。 可以在同一形状的任意两个张量上调用按元素操作。
x = tf.constant([1.0, 2, 4, 8])
y = tf.constant([2.0, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 3., 4., 6., 10.], dtype=float32)>,
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-1., 0., 2., 6.], dtype=float32)>,
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 2., 4., 8., 16.], dtype=float32)>,
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0.5, 1. , 2. , 4. ], dtype=float32)>,
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 1., 4., 16., 64.], dtype=float32)>)
#求幂运算也可以如下
tf.exp(x)
有时,想[通过逻辑运算符构建二元张量]。 以X == Y为例: 对于每个位置,如果X和Y在该位置相等,则新张量中相应项的值为1。 这意味着逻辑语句X == Y在该位置处为真,否则该位置为0。
X = tf.reshape(tf.range(12, dtype=tf.float32), (3, 4))
Y = tf.constant([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X == Y
对张量中的所有元素进行求和,会产生一个单元素张量。
tf.reduce_sum(X)
2.张量连结(拼接)
把多个张量连结(concatenate)在一起], 把它们端对端地叠起来形成一个更大的张量。 只需要提供张量列表,并给出沿哪个轴连结。
X = tf.reshape(tf.range(12, dtype=tf.float32), (3, 4))
Y = tf.constant([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X)
print(Y)
print("\n")
print(tf.concat([X, Y], axis=1))
tf.concat([X, Y], axis=0)
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]], shape=(3, 4), dtype=float32)
tf.Tensor(
[[2. 1. 4. 3.]
[1. 2. 3. 4.]
[4. 3. 2. 1.]], shape=(3, 4), dtype=float32)
tf.Tensor(
[[ 0. 1. 2. 3. 2. 1. 4. 3.]
[ 4. 5. 6. 7. 1. 2. 3. 4.]
[ 8. 9. 10. 11. 4. 3. 2. 1.]], shape=(3, 8), dtype=float32)
<tf.Tensor: shape=(6, 4), dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]], dtype=float32)>
3.张量的广播机制
在某些情况下,[即使形状不同,仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作]。 这种机制的工作方式如下:
- 通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状;
- 对生成的数组执行按元素操作。
a和b分别是 3×1 和 1×2矩阵,如果让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的 3×2矩阵,如下所示:矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
a = tf.reshape(tf.range(3), (3, 1))
b = tf.reshape(tf.range(2), (1, 2))
print(a, b)
a + b
返回:
(<tf.Tensor: shape=(3, 1), dtype=int32, numpy=
array([[0],
[1],
[2]])>,
<tf.Tensor: shape=(1, 2), dtype=int32, numpy=array([[0, 1]])>)
<tf.Tensor: shape=(3, 2), dtype=int32, numpy=
array([[0, 1],
[1, 2],
[2, 3]])>
三、张量的数据操作
1. 张量的访问:索引和切片
张量中的元素可以通过索引访问。 与任何Python数组一样:第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素。
可以用[-1]选择最后一个元素,可以用[1:3]选择第二个和第三个元素:
X = tf.reshape(tf.range(12, dtype=tf.float32), (3, 4))
X[-1], X[1:3]
索引、切片可以用来访问元素也可以用来更改和删除元素,但仅在Variable类型的张量中可进行更改和删除元素
X_var = tf.Variable(X)
print(X_var)
X_var[1, 2].assign(9)
X_var
<tf.Variable 'Variable:0' shape=(3, 4) dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]], dtype=float32)>
<tf.Variable 'Variable:0' shape=(3, 4) dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 5., 9., 7.],
[ 8., 9., 10., 11.]], dtype=float32)>
为多个元素赋值相同的值,只需要索引所有元素,然后为它们赋值。] 例如,[0:2, :]访问第1行和第2行,其中“:”代表沿轴1(列)的所有元素。
X_var = tf.Variable(X)
print(X_var)
X_var[0:2, :].assign(tf.ones(X_var[0:2,:].shape, dtype = tf.float32) * 12)
X_var
<tf.Variable 'Variable:0' shape=(3, 4) dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]], dtype=float32)>
<tf.Variable 'Variable:0' shape=(3, 4) dtype=float32, numpy=
array([[12., 12., 12., 12.],
[12., 12., 12., 12.],
[ 8., 9., 10., 11.]], dtype=float32)>
2.张量和其他python对象互相转换
将深度学习框架定义的张量[转换为NumPy张量(ndarray)]很容易,反之也同样容易。 转换后的结果不共享内存。
(1)将张量和numpy数组互相转换
print(type(X))
A = X.numpy()
B = tf.constant(A)
type(A), type(B)
<class 'tensorflow.python.framework.ops.EagerTensor'>
(numpy.ndarray, tensorflow.python.framework.ops.EagerTensor)
(2)将大小为1的张量转换为Python标量
a = tf.constant([3.5]).numpy()
a, a.item(), float(a), int(a)
(3)将pandas的df转换为张量
首先读取数据并预处理,这里不多说,很简单,基操。
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
# 如果没有安装pandas,只需取消对以下行的注释来安装pandas
# !pip install pandas
import pandas as pd
data = pd.read_csv(data_file)
print(data)
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
print(inputs)
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
print(inputs)
print(outputs)
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
0 127500
1 106000
2 178100
3 140000
Name: Price, dtype: int64
现在inputs和outputs中的所有条目都是数值类型,它们可以转换为张量格式。
import tensorflow as tf
X, y = tf.constant(inputs.values), tf.constant(outputs.values)
X, y
(<tf.Tensor: shape=(4, 3), dtype=float64, numpy=
array([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]])>,
<tf.Tensor: shape=(4,), dtype=int64, numpy=array([127500, 106000, 178100, 140000], dtype=int64)>)
3.可变张量与不可变张量(深浅复制、涉及节省内存和优化程序必需)
TensorFlow中的Tensors是不可变的,也不能被赋值。 TensorFlow中的Variables是支持赋值的可变容器。 请记住,TensorFlow中的梯度不会通过Variable反向传播。
运行一些操作可能会导致为新结果分配内存,这种情况下内存会快速增长、从而导致程序崩溃的可能性,但是有时候又需要使用新的张量结果、有时候又需要使用旧的张量结果 例如,如果用Y = X + Y,将取消引用Y指向的原有张量,而是指向新分配的内存处的张量。
before = id(Y)
Y = Y + X
id(Y) == before
返回
False
Variables是TensorFlow中的可变容器,它们提供了一种存储模型参数的方法。 如此一来,在机器学习中,可能有数百兆的参数,并且在一秒内多次更新所有参数。通常情况下,希望原地执行这些更新,Variables张量就能做到此需求;
Z = tf.Variable(tf.zeros_like(Y))
print('id(Z):', id(Z))
Z.assign(X + Y)
print('id(Z):', id(Z))
id(Z): 139712800290752
id(Z): 139712800290752
即使你将状态持久存储在Variable中, 你也可能希望避免为不是模型参数的张量过度分配内存,从而进一步减少内存使用量。由于TensorFlow的Tensors是不可变的,而且梯度不会通过Variable流动, 因此TensorFlow没有提供一种明确的方式来原地运行单个操作。
TensorFlow提供了tf.function修饰符, 将计算封装在TensorFlow图中,该图在运行前经过编译和优化。 这允许TensorFlow删除未使用的值,并复用先前分配的且不再需要的值。 这样可以最大限度地减少TensorFlow计算的内存开销。
@tf.function
def computation(X, Y):
Z = tf.zeros_like(Y) # 这个未使用的值将被删除
A = X + Y # 当不再需要时,分配将被复用
B = A + Y
C = B + Y
return C + Y
computation(X, Y)
<tf.Tensor: shape=(3, 4), dtype=float32, numpy=
array([[ 8., 9., 26., 27.],
[24., 33., 42., 51.],
[56., 57., 58., 59.]], dtype=float32)>
四、线性代数
除了按元素计算外,还可以执行线性代数运算,包括向量点积和矩阵乘法。
1.标量、向量、矩阵、张量
(1)标量
严格来说,仅包含一个数值被称为标量(scalar),标量由只有一个元素的张量表示。
import tensorflow as tf
x = tf.constant(3.0)
y = tf.constant(2.0)
x + y, x * y, x / y, x**y
(<tf.Tensor: shape=(), dtype=float32, numpy=5.0>,
<tf.Tensor: shape=(), dtype=float32, numpy=6.0>,
<tf.Tensor: shape=(), dtype=float32, numpy=1.5>,
<tf.Tensor: shape=(), dtype=float32, numpy=9.0>)
(2)向量
向量可以被视为标量值组成的列表。 这些标量值被称为向量的元素(element)或分量(component)。 当向量表示数据集中的样本时,它们的值具有一定的现实意义。 例如,如果正在训练一个模型来预测贷款违约风险,可能会将每个申请人与一个向量相关联, 其分量与其收入、工作年限、过往违约次数和其他因素相对应。
通过一维张量表示向量。一般来说,张量可以具有任意长度,取决于机器的内存限制。通过张量的索引来访问任一元素。
x = tf.range(4)
x
x[3]
<tf.Tensor: shape=(4,), dtype=int32, numpy=array([0, 1, 2, 3])>
<tf.Tensor: shape=(), dtype=int32, numpy=3>
使用下标来引用向量的任一元素,例如可以通过 𝑥𝑖来引用第 𝑖个元素。 注意,元素 𝑥𝑖是一个标量,所以在引用它时不会加粗。 大量文献认为列向量是向量的默认方向:
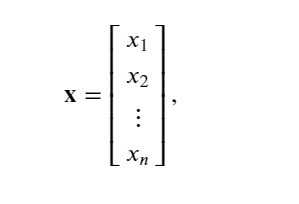
(3)矩阵
矩阵:正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。 矩阵,我们通常用粗体、大写字母来表示 (例如, 𝐗 、 𝐘 和 𝐙 ), 在代码中表示为具有两个轴的张量。

𝐀 的形状是( 𝑚 , 𝑛 )或 𝑚×𝑛 。 当矩阵具有相同数量的行和列时,其形状将变为正方形; 因此,它被称为方阵(square matrix)。当调用函数来实例化张量时, 可以[通过指定两个分量 𝑚 和 𝑛 来创建一个形状为 𝑚×𝑛 的矩阵]。
A = tf.reshape(tf.range(20), (5, 4))
A
矩阵转置:当交换矩阵的行和列时,结果称为矩阵的转置(transpose)。
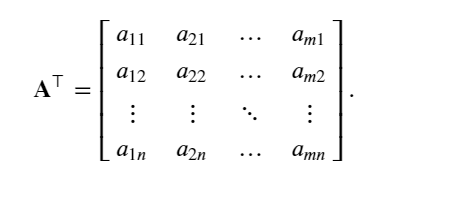
tf.transpose(A)
(4)张量
就像向量是标量的推广,矩阵是向量的推广一样,可以构建具有更多轴的数据结构。当开始处理图像时,张量将变得更加重要,图像以 𝑛 维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。
X = tf.reshape(tf.range(24), (2, 3, 4))
X
<tf.Tensor: shape=(2, 3, 4), dtype=int32, numpy=
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])>
2.张量计算的基本性质
任何按元素的一元运算都不会改变其操作数的形状。 同样,给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。
(1)直接赋值旧变量到形变量、不会分配新内存
A = tf.reshape(tf.range(20, dtype=tf.float32), (5, 4))
print(A)
B = A # 不能通过分配新内存将A克隆到B
id(A)==id(B) # 两个变量的内存地址一样,没有产生新的内存地址
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]
[16. 17. 18. 19.]], shape=(5, 4), dtype=float32)
True
(2)两个矩阵的Hadamard积(按元素乘法)
两个矩阵的按元素乘法称为Hadamard积(Hadamard product)(数学符号 ⊙):

(3)矩阵与标量的运算
将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。加减乘除、次幂等皆不会改变张量的形状。
a = 2
X = tf.reshape(tf.range(24), (2, 3, 4))
print(X)
a + X, (a * X).shape
tf.Tensor(
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]], shape=(2, 3, 4), dtype=int32)
(<tf.Tensor: shape=(2, 3, 4), dtype=int32, numpy=
array([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]])>,
TensorShape([2, 3, 4]))
X.shape,(a / X).shape,(a-X).shape
(TensorShape([2, 3, 4]), TensorShape([2, 3, 4]), TensorShape([2, 3, 4]))
(4)降维计算
以对任意张量进行的一个有用的操作是计算其元素的和。 数学表示法使用 ∑ 符号表示求和。
当然,也可以计算均值等。
x = tf.range(4, dtype=tf.float32)
x, tf.reduce_sum(x)
(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>,
<tf.Tensor: shape=(), dtype=float32, numpy=6.0>)
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。 还可以指定张量沿哪一个轴来通过求和降低维度。
print(A)
A_sum_axis0 = tf.reduce_sum(A, axis=0)
A_sum_axis0, A_sum_axis0.shape
#指定axis=1将通过汇总所有列的元素降维(轴1)。因此,输入轴1的维数在输出形状中消失。
A_sum_axis1 = tf.reduce_sum(A, axis=1)
A_sum_axis1, A_sum_axis1.shape
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]
[16. 17. 18. 19.]], shape=(5, 4), dtype=float32)
(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([40., 45., 50., 55.], dtype=float32)>,
TensorShape([4]))
(<tf.Tensor: shape=(5,), dtype=float32, numpy=array([ 6., 22., 38., 54., 70.], dtype=float32)>,
TensorShape([5]))
tf.reduce_sum(A, axis=[0, 1]) # 结果和tf.reduce_sum(A)相同
<tf.Tensor: shape=(), dtype=float32, numpy=190.0>
同样,计算平均值的函数也可以沿指定轴降低张量的维度。
tf.reduce_mean(A, axis=0), tf.reduce_sum(A, axis=0) / A.shape[0]
(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 8., 9., 10., 11.], dtype=float32)>,
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 8., 9., 10., 11.], dtype=float32)>)
(5)非降维求和
有时在调用函数来计算总和或均值时保持轴数不变会很有用。
print(A)
sum_A = tf.reduce_sum(A, axis=1, keepdims=True)
sum_A
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]
[16. 17. 18. 19.]], shape=(5, 4), dtype=float32)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[ 6.],
[22.],
[38.],
[54.],
[70.]], dtype=float32)>
想沿某个轴计算A元素的累积总和, 比如axis=0(按行计算),可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。
A,tf.cumsum(A, axis=0),tf.cumsum(A, axis=1)
(<tf.Tensor: shape=(5, 4), dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]], dtype=float32)>,
<tf.Tensor: shape=(5, 4), dtype=float32, numpy=
array([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]], dtype=float32)>,
<tf.Tensor: shape=(5, 4), dtype=float32, numpy=
array([[ 0., 1., 3., 6.],
[ 4., 9., 15., 22.],
[ 8., 17., 27., 38.],
[12., 25., 39., 54.],
[16., 33., 51., 70.]], dtype=float32)>)
(6)点积(Dot Product)
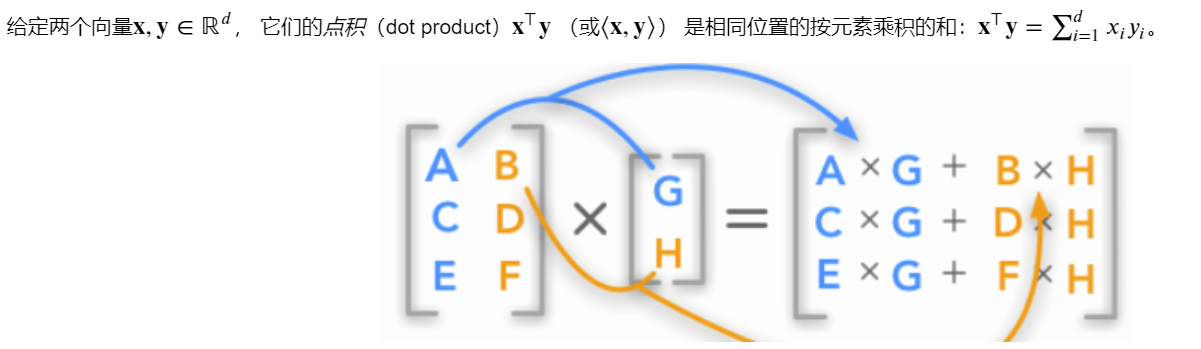
y = tf.ones(4, dtype=tf.float32)
print(x, y)
tf.tensordot(x, y, axes=1)#点积
tf.Tensor([0. 1. 2. 3.], shape=(4,), dtype=float32) tf.Tensor([1. 1. 1. 1.], shape=(4,), dtype=float32)
<tf.Tensor: shape=(), dtype=float32, numpy=6.0>
(7)矩阵-向量积

使用与点积相同的matvec函数。 当为矩阵A和向量x调用tf.linalg.matvec(A, x)时,会执行矩阵-向量积。 注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
print(A.shape, x.shape)
print(A,x)
tf.linalg.matvec(A, x)
(5, 4) (4,)
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]
[16. 17. 18. 19.]], shape=(5, 4), dtype=float32) tf.Tensor([0. 1. 2. 3.], shape=(4,), dtype=float32)
<tf.Tensor: shape=(5,), dtype=float32, numpy=array([ 14., 38., 62., 86., 110.], dtype=float32)>
(8)矩阵-矩阵乘积(矩阵乘法)
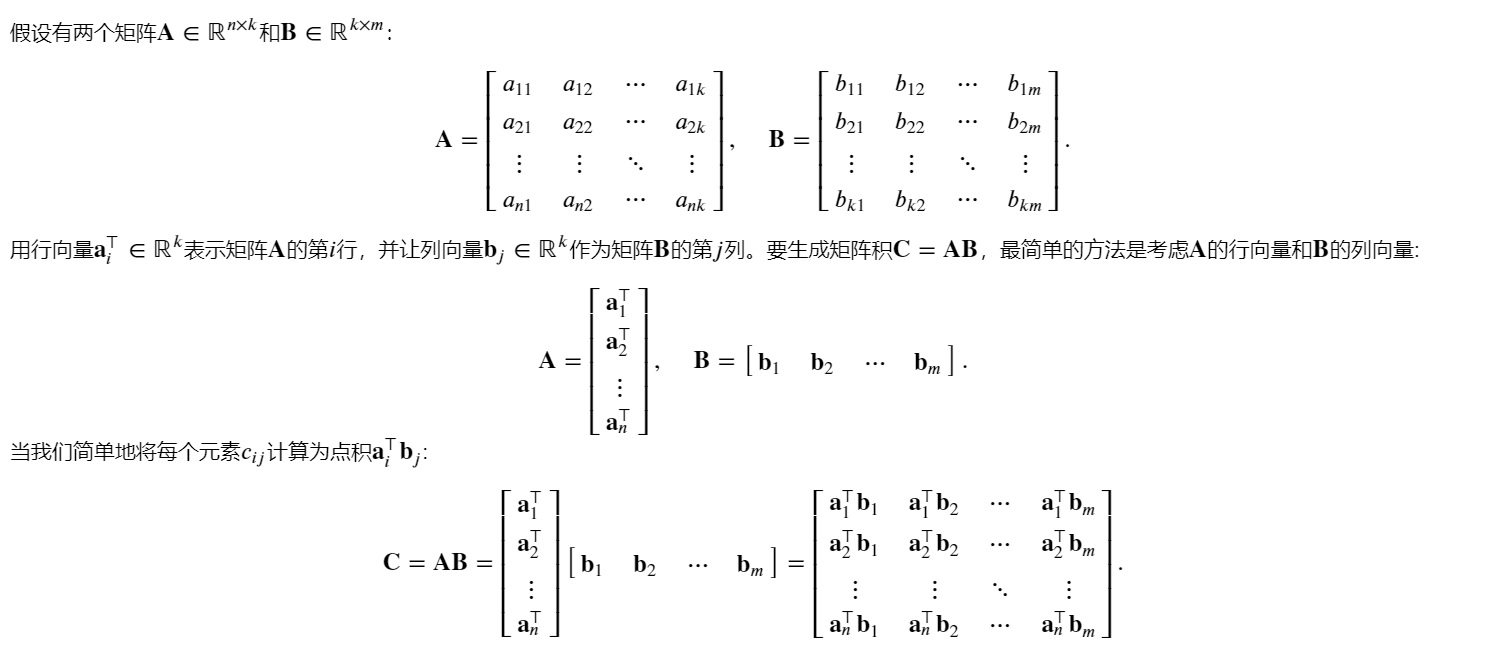
可以将矩阵-矩阵乘法 𝐀𝐁 看作简单地执行 𝑚次矩阵-向量积,并将结果拼接在一起,形成一个 𝑛×𝑚
矩阵。 在下面的代码中,我们在A和B上执行矩阵乘法。 这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。 两者相乘后,我们得到了一个5行3列的矩阵。
B = tf.ones((4, 3), tf.float32)
print(A,B)
tf.matmul(A, B)
tf.Tensor(
[[ 0. 1. 2. 3.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]
[12. 13. 14. 15.]
[16. 17. 18. 19.]], shape=(5, 4), dtype=float32) tf.Tensor(
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]], shape=(4, 3), dtype=float32)
<tf.Tensor: shape=(5, 3), dtype=float32, numpy=
array([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]], dtype=float32)>
(9)范数
线性代数中最有用的一些运算符是范数(norm)。 非正式地说,向量的范数是表示一个向量有多大。 这里考虑的大小(size)概念不涉及维度,而是分量的大小。

范数听起来很像距离的度量。 欧几里得距离和毕达哥拉斯定理中的非负性概念和三角不等式可能会给出一些启发。 事实上,欧几里得距离是一个 𝐿2范数。度学习中更经常地使用 𝐿2 范数的平方,也会经常遇到 𝐿1 范数,它表示为向量元素的绝对值之和。
计算L2范数:
u = tf.constant([3.0, -4.0])
tf.norm(u)
<tf.Tensor: shape=(), dtype=float32, numpy=5.0>
计算L1范数:
tf.reduce_sum(tf.abs(u))
<tf.Tensor: shape=(), dtype=float32, numpy=7.0>