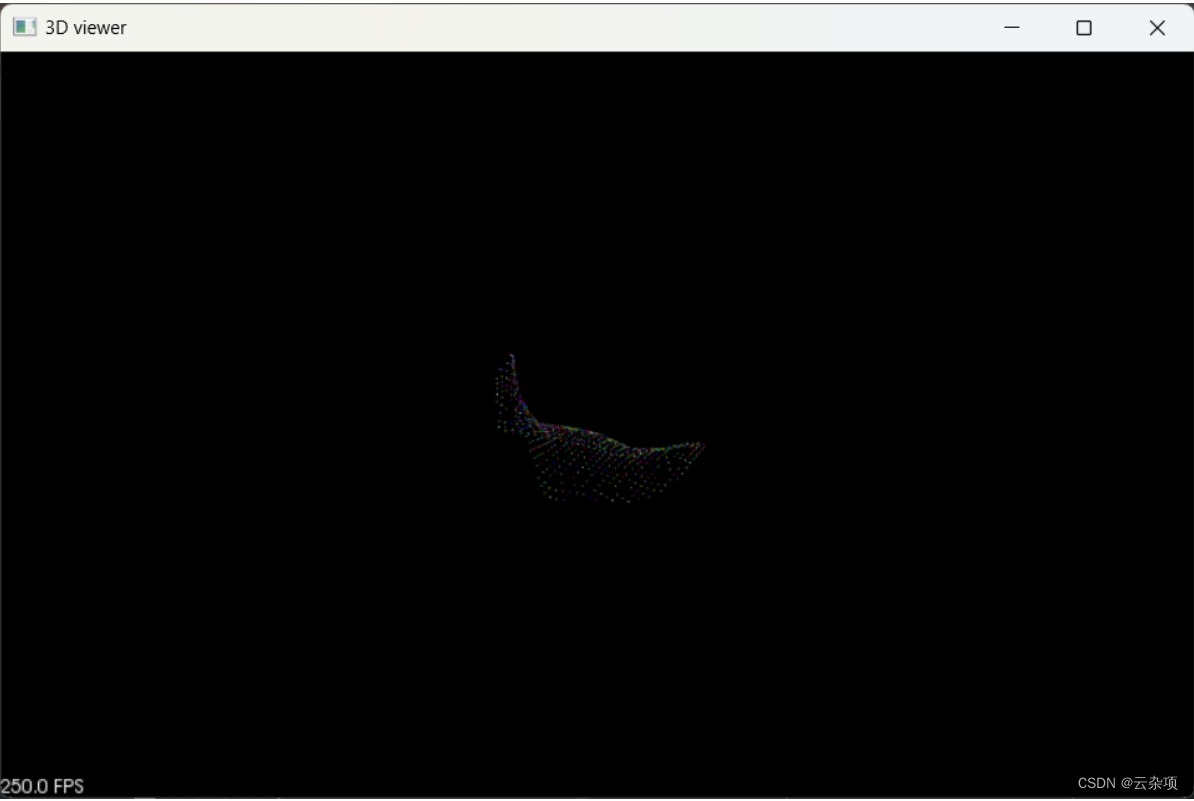
今天绘制一个砂轮，其轮廓由两条直线段和两段圆弧构成，圆弧分别与直线相切，两条圆弧之间相交而非相切。建模思路是：先给定两条直线段的起始点及长度，画出直线段，然后给定其中一圆弧的半径及圆心角，依据此计算出该圆弧圆心，接着求出另一圆弧圆心和半径，最后创建边和环，对环进行环形扫掠，得到砂轮实体。构建过程主要涉及：

直线、直线段创建

直线的创建通常涉及gp_Lin类，它代表一个无限长的直线。而直线段的创建则涉及Geom_TrimmedCurve类，它是表示修剪曲线的基类，可以用于表示直线段、圆弧段等。

圆、圆弧创建

创建圆和圆弧涉及使用gp_Circ类来表示圆，以及Geom_TrimmedCurve类来表示圆弧。

求直线上一点的垂线

平面内两直线相交求交点

创建TopoDS_Edge

TopoDS_Edge 是表示拓扑边缘的类，通常它是构成几何形状边界的一部分。要创建一个 TopoDS_Edge 对象，你通常需要从几何形状（如线段、圆弧、圆、椭圆等）开始，并将其转换为拓扑边缘。

创建TopoDS_Wire

TopoDS_Wire表示一个由有序的边(edge)序列构成的拓扑线框。创建TopoDS_Wire通常涉及使用BRep类库中的构造器来构建一系列的边，并将它们组合成一个线框。

创建旋转扫掠

建旋转扫掠（也称为旋转体或回转体）通常涉及使用BRepPrimAPI_MakeRevolution类。这个类允许围绕一个指定的轴旋转一个二维轮廓来创建一个三维实体。

前面已经使用SW绘制过：Solidworks二次开发：python画砂轮

基于C++的具体实现如下：

#include <GC_MakeSegment.hxx>
#include <BRepBuilderAPI_MakeVertex.hxx>
#include <gp_Circ.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <GC_MakeArcOfCircle.hxx>
#include <gp_Lin2d.hxx>
#include <gp_Pnt2d.hxx>
#include <BRepBuilderAPI_MakeWire.hxx>
#include <gp_Lin.hxx>
#include <IntAna2d_AnaIntersection.hxx>
#include <BRepPrimAPI_MakeRevol.hxx>
​
#include"Viewer.h"
​
​
int main(int argc, char* argv[])
{
    Standard_Real Line1_angle = 280 * M_PI / 180;
    Standard_Real Line1_length = 0.762;
    Standard_Real Line2_angle = 236 * M_PI / 180;
    Standard_Real Line2_length = 0.9081;
    Standard_Real Arc1_r = 0.159;
    Standard_Real Arc1_angle = 48;
    gp_Pnt Line1_p1(-0.9832 / 2, 0, 0);
    gp_Pnt Line2_p1(0.9832 / 2, 0, 0);
    gp_Lin Line1(Line1_p1, gp_Dir(cos(Line1_angle), sin(Line1_angle), 0.));
    gp_Lin Line2(Line2_p1, gp_Dir(cos(Line2_angle), sin(Line2_angle), 0.));
    Handle(Geom_TrimmedCurve) L1 = GC_MakeSegment(Line1, 0., Line1_length);
    TopoDS_Edge L1e = BRepBuilderAPI_MakeEdge(L1);
    Handle(Geom_TrimmedCurve) L2 = GC_MakeSegment(Line2, 0., Line2_length);
    TopoDS_Edge L2e = BRepBuilderAPI_MakeEdge(L2);
    gp_Pnt l1end = L1->EndPoint();
    gp_Pnt l2end = L2->EndPoint();
    gp_Lin Line1v(l1end, gp_Dir(cos(Line1_angle+M_PI_2), sin(Line1_angle+ M_PI_2), 0.));
    gp_Lin2d Line2v(gp_Pnt2d(l2end.X(), l2end.Y()), gp_Dir2d(cos(Line2_angle- M_PI_2), sin(Line2_angle- M_PI_2)));
    gp_Lin Line2v3d(l2end, gp_Dir(cos(Line2_angle - M_PI_2), sin(Line2_angle - M_PI_2),0.));
    Handle(Geom_TrimmedCurve) L1v = GC_MakeSegment(Line1v, 0., Arc1_r);
    gp_Pnt l1vend = L1v->EndPoint();
    gp_Circ c1(gp_Ax2(l1vend,gp_Dir(0,0,1)), Arc1_r);
    Handle(Geom_TrimmedCurve) c1c = GC_MakeArcOfCircle(c1, l1end, Arc1_angle, 1);
    gp_Pnt c1end = c1c->EndPoint();
    gp_Lin2d Line3(gp_Pnt2d(c1end.X(),c1end.Y()),gp_Dir2d(l2end.X() - c1end.X(), l2end.Y() - c1end.Y()));
    gp_Lin2d Line3v = Line3.Normal(gp_Pnt2d((l2end.X() + c1end.X())/2,(l2end.Y() + c1end.Y())/2));
    IntAna2d_AnaIntersection aIntAna;
    aIntAna.Perform(Line2v, Line3v); 
    IntAna2d_IntPoint aIntPoint = aIntAna.Point(1);
    gp_Pnt o2(aIntPoint.Value().X(), aIntPoint.Value().Y(),0.);
    Handle(Geom_TrimmedCurve) L2v = GC_MakeSegment(Line2v3d, l2end, o2);
    Standard_Real r2=L2v->LastParameter();
    gp_Circ c2(gp_Ax2(o2, gp_Dir(0, 0, 1)), r2);
    Handle(Geom_TrimmedCurve) c2c = GC_MakeArcOfCircle(c2, c1end, l2end, 1);
​
    TopoDS_Edge c1ce = BRepBuilderAPI_MakeEdge(c1c);
    TopoDS_Edge L1ev = BRepBuilderAPI_MakeEdge(L1v);
    TopoDS_Edge c2ce = BRepBuilderAPI_MakeEdge(c2c);
​
    gp_Pnt Line1_up(-0.9832 / 2, 5, 0);
    gp_Pnt Line2_up(0.9832 / 2, 5, 0);
    TopoDS_Edge anEdge1 = BRepBuilderAPI_MakeEdge(Line1_p1, Line1_up);
    TopoDS_Edge anEdge2 = BRepBuilderAPI_MakeEdge(Line1_up, Line2_up);
    TopoDS_Edge anEdge3 = BRepBuilderAPI_MakeEdge(Line2_up, Line2_p1);
    TopTools_ListOfShape listEdge;
    listEdge.Append(anEdge1);
    listEdge.Append(anEdge2);
    listEdge.Append(anEdge3);
    listEdge.Append(L1e);
    listEdge.Append(c1ce);
    listEdge.Append(c2ce);
    listEdge.Append(L2e);
    BRepBuilderAPI_MakeWire mw;
    mw.Add(listEdge);
    mw.Build();
    TopoDS_Shape gwheel = BRepPrimAPI_MakeRevol(mw, gp_Ax1(gp_Pnt(0, 5, 0), gp_Dir(1, 0, 0)), 2*M_PI);
    Viewer vout(50, 50, 500, 500);
    vout << gwheel;
   
    vout.StartMessageLoop();
    return 0;
}
​