政安晨的个人主页：政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正，让小伙伴们一起学习、交流进步，不论是学业还是工作都取得好成绩！
前言
咱们这个系列的前面几篇机器学习示例演绎的文章中，演绎的都是分类问题，其目标是预测输入数据点所对应的单一离散标签。
其实还有另一种常见的机器学习问题是回归（regression）问题，它预测的是一个连续值，而不是离散标签，比如根据气象数据预测明日气温，或者根据软件说明书预测完成软件项目所需时间。
这个系列的前面三篇文章为：
政安晨：【示例演绎机器学习】（一）—— 剖析神经网络：学习核心的Keras API
https://blog.csdn.net/snowdenkeke/article/details/136187781政安晨：【示例演绎机器学习】（二）—— 神经网络的二分类问题示例 (影评分类)https://blog.csdn.net/snowdenkeke/article/details/136204994政安晨：【示例演绎机器学习】（三）—— 神经网络的多分类问题示例 (新闻分类)https://blog.csdn.net/snowdenkeke/article/details/136218745咱们准备好环境后开始机器学习的演绎。
导入数据集
本节将尝试预测上世纪某个时期波士顿郊区房价的中位数，已知当时郊区的一些数据点，如犯罪率、地方房产税率等。本节用到的数据集与前两个例子有一个有趣的区别。
它包含的数据点相对较少，只有506个，划分为404个训练样本和102个测试样本。
输入数据的每个特征（比如犯罪率）都有不同的取值范围。
有的特征是比例，取值在0和1之间；
有的取值在1和12之间；
还有的取值在0和100之间。
我们首先加载波士顿房价数据集，如代码如下所示：
（加载波士顿房价数据集）
from tensorflow.keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = (
boston_housing.load_data())
咱们来看一下数据：
可以看到，我们有404个训练样本和102个测试样本，每个样本都有13个数值特征，比如人均犯罪率、住宅的平均房间数、高速公路可达性等。
目标是房价中位数，单位是千美元。
房价大都介于10 000美元～50 000美元。如果你觉得这很便宜，请不要忘记当时是20世纪70年代中期，而且这些价格没有按通货膨胀进行调整。
准备数据
将取值范围差异很大的数据输入到神经网络中，这是有问题的。
模型可能会自动适应这种取值范围不同的数据，但这肯定会让学习变得更加困难。
对于这类数据，普遍采用的最佳处理方法是对每个特征进行标准化，即对于输入数据的每个特征（输入数据矩阵的每一列），减去特征平均值，再除以标准差，这样得到的特征平均值为0，标准差为1。
用NumPy可以很容易实现数据标准化，如下代码所示：
（数据标准化）
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std注意，对测试数据进行标准化的平均值和标准差都是在训练数据上计算得到的。
在深度学习工作流程中，你不能使用在测试数据上计算得到的任何结果，即使是像数据标准化这么简单的事情也不行。
构建模型
由于样本数量很少，因此我们将使用一个非常小的模型。它包含两个中间层，每层有64个单元，如下代码所示（模型定义）：
（一般来说，训练数据越少，过拟合就会越严重，而较小的模型可以降低过拟合。）
from tensorflow import keras
from tensorflow.keras import layers
def build_model():
# 由于需要将同一个模型多次实例化，因此我们用一个函数来构建模型
model = keras.Sequential([
layers.Dense(64, activation="relu"),
layers.Dense(64, activation="relu"),
layers.Dense(1)
])
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
return model模型的最后一层只有一个单元且没有激活，它是一个线性层。
这是标量回归（标量回归是预测单一连续值的回归）的典型设置。
添加激活函数将限制输出范围。
如果向最后一层添加sigmoid激活函数，那么模型只能学会预测0到1的值。这里最后一层是纯线性的，所以模型可以学会预测任意范围的值。
注意，我们编译模型用的是mse损失函数，即均方误差（mean squared error，MSE），预测值与目标值之差的平方。这是回归问题常用的损失函数。
在训练过程中还要监控一个新指标：平均绝对误差（mean absolute error，MAE）。
它是预测值与目标值之差的绝对值。如果这个问题的MAE等于0.5，就表示预测房价与实际价格平均相差500美元。
利用K折交叉验证来验证你的方法
为了在调节参数（比如训练轮数）的同时对模型进行评估，我们可以将数据划分为训练集和验证集，正如前面的例子所做的那样。
但由于数据点很少，验证集会非常小（比如大约100个样本），因此验证分数可能会有很大波动，这取决于我们所选择的验证集和训练集。也就是说，验证分数对于验证集的划分方式可能会有很大的方差，这样我们就无法对模型进行可靠的评估。
在这种情况下，最佳做法是使用K折交叉验证，如下图所示：
这种方法将可用数据划分为K个分区（K通常取4或5），实例化K个相同的模型，然后将每个模型在K-1个分区上训练，并在剩下的一个分区上进行评估。模型的验证分数等于这K个验证分数的平均值。
这种方法的代码实现很简单，如下代码所示（K折交叉验证）：
k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
print(f"Processing fold #{i}")
# 准备验证数据：第k个分区的数据
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# 准备训练数据：其余所有分区的数据
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
# 构建Keras模型（已编译）
model = build_model()
# 训练模型（静默模式，verbose=0）
model.fit(partial_train_data, partial_train_targets,
epochs=num_epochs, batch_size=16, verbose=0)
# 验证数据上评估模型
val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
all_scores.append(val_mae)演绎：
设置num_epochs = 100，运行结果如下：
每次运行模型得到的验证分数确实有很大差异，从2.1到3.1不等。
平均分数（2.6）是比单一分数更可靠的指标——这就是K折交叉验证的核心要点。
在这个例子中，预测房价与实际房价平均相差2600美元，考虑到实际房价范围是10 000美元～50000美元，这一差别还是很大的。
我们让模型训练时间更长一点：500轮。为了记录模型每轮的表现，我们需要修改训练循环，在每轮都保存每折的验证分数，如下代码所示（保存每折的验证分数）：
num_epochs = 500
all_mae_histories = []
for i in range(k):
print(f"Processing fold #{i}")
# 准备验证数据：第k个分区的数据
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# 准备训练数据：其余所有分区的数据
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
# 构建Keras模型（已编译）
model = build_model()
# 训练模型（静默模式，verbose=0）
history = model.fit(partial_train_data, partial_train_targets,
validation_data=(val_data, val_targets),
epochs=num_epochs, batch_size=16, verbose=0)
mae_history = history.history["val_mae"]
all_mae_histories.append(mae_history)演绎：
然后，计算每轮所有折MAE的平均值，如下代码所示：
（计算每轮的K折验证分数平均值）
average_mae_history = [
np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]我们来画图看看，如下代码所示：
（绘制验证MAE曲线）
import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel("Epochs")
plt.ylabel("Validation MAE")
plt.show()
由于比例问题，前几轮的验证MAE远大于后面的轮次，很难看清这张图的规律。我们忽略前10个数据点，因为它们的取值范围与曲线上的其他点不同，如下代码所示：
（绘制验证MAE曲线（剔除前10个数据点））
truncated_mae_history = average_mae_history[10:]
plt.plot(range(1, len(truncated_mae_history) + 1), truncated_mae_history)
plt.xlabel("Epochs")
plt.ylabel("Validation MAE")
plt.show()
从上图可以看出，验证MAE在120～140轮（包含剔除的那10轮）后不再显著降低，再之后就开始过拟合了。
完成模型调参之后（除了轮数，还可以调节中间层大小），你可以使用最佳参数在所有训练数据上训练最终的生产模型，然后查看模型在测试数据上的表现，如下代码所示：
（训练最终模型）
# 一个全新的已编译模型
model = build_model()
# 在所有训练数据上训练模型
model.fit(train_data, train_targets,
epochs=130, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)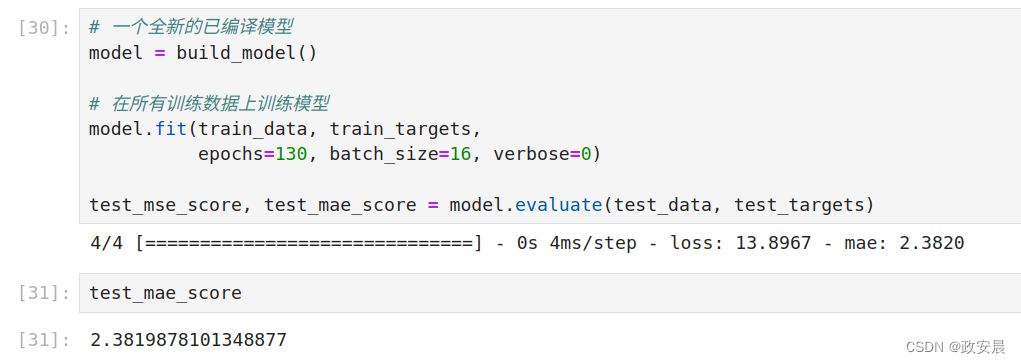
预测房价和实际房价还是相差不到2500美元。不过有进步！就像前两个任务一样，你可以尝试改变模型的层数或每层的单元个数，看是否能够降低测试误差。
对新数据进行预测
在调用二分类模型的predict()时，每个输入样本都得到一个介于0和1之间的标量值。
对于多分类模型，每个样本都得到一个在所有类别上的概率分布。对于这个标量回归模型，predict()返回的是模型对样本价格的猜测，单位是千美元。
predictions = model.predict(test_data)
predictions[0]模型预测，测试集中的第一所房子的价格约为10 000美元。
结论
回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差（MSE）。
同样，回归问题使用的评估指标也与分类问题不同。显然，精度的概念不再适用于回归问题。常用的回归指标是平均绝对误差（MAE）。如果输入数据的特征具有不同的取值范围，那么应该先进行预处理，对每个特征单独进行缩放。如果可用的数据很少，那么K折交叉验证是评估模型的可靠方法。
如果可用的训练数据很少，那么最好使用中间层较少（通常只有一两个）的小模型，以避免严重的过拟合。
