代码随想录算法训练营第四十天 | 343. 整数拆分、 96.不同的二叉搜索树
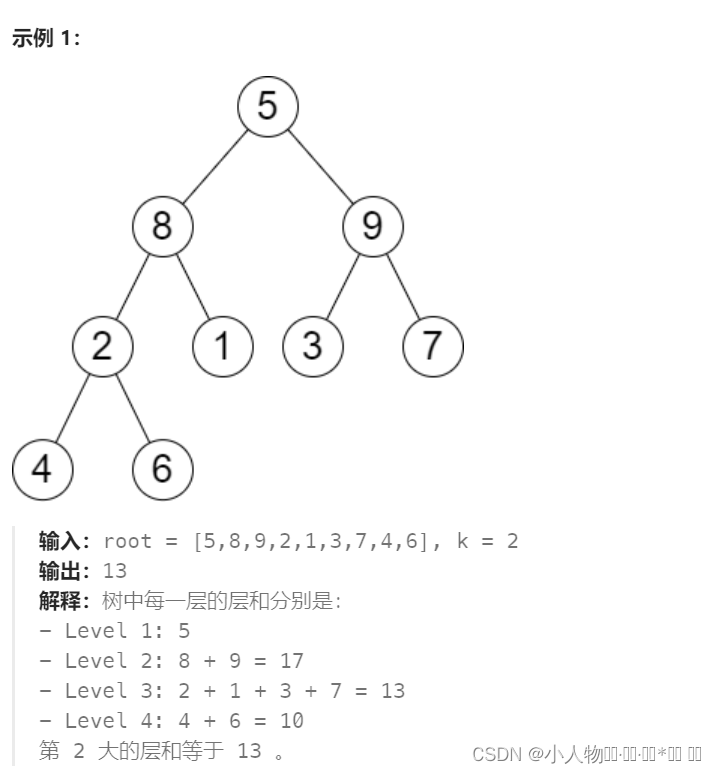
343. 整数拆分
题目链接:343. 整数拆分 - 力扣(LeetCode)
例如 n = 10, 可以拆分为 3 * dp[7] 。因为dp[7]之前已经计算过最大= 3 * 4, 所以dp[10] = 3 * 3 * 4
class Solution {
public int integerBreak(int n) {
//dp[i] 为正整数 i 拆分后的结果的最大乘积
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i <= n; i++) {
for(int j = 1; j <= i-j; j++) {
// 这里的 j 其实最大值为 i-j,再大只不过是重复而已,
//并且,在本题中,我们分析 dp[0], dp[1]都是无意义的,
//j 最大到 i-j,就不会用到 dp[0]与dp[1]
dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
// j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ,再相乘
//而j * dp[i - j]是将 i 拆分成两个以上的个数,再相乘。
}
}
return dp[n];
}
}
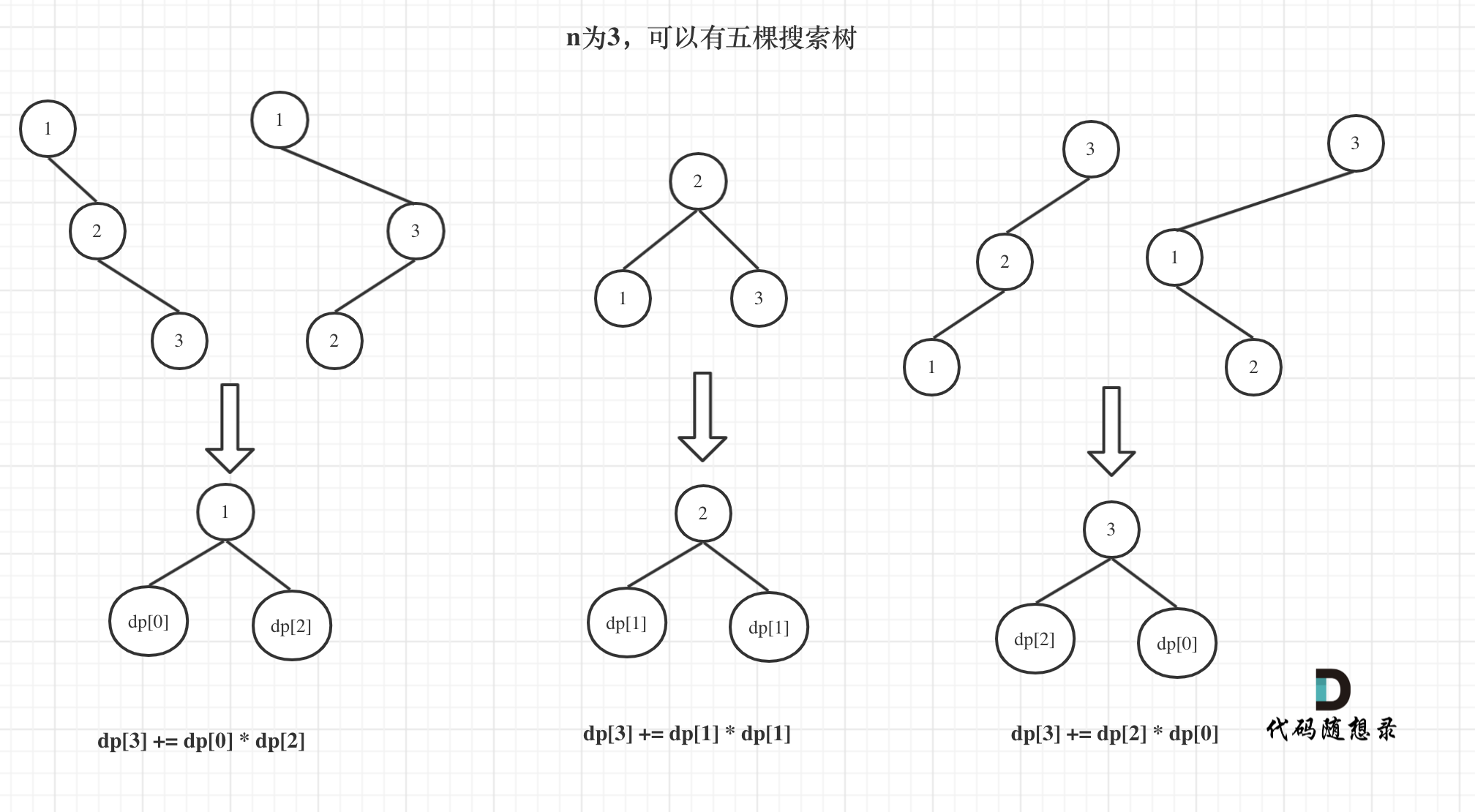
96.不同的二叉搜索树
题目链接:96. 不同的二叉搜索树 - 力扣(LeetCode)
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
//初始化 dp 数组
dp[0] = 1;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= i; ++j) {
// 对于第i个节点,需要考虑1作为根节点直到i作为根节点的情况,所以需要累加
// 一共i个节点,对于根节点j时,左子树的节点个数为j-1,右子树的节点个数为i-j
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}
总结
}
return dp[n];
}
}
## 总结
今天的两题类似,题目读起来比较难以理解,但是掌握了dp递推公式的就能简单解出(能想到递推公式还是难呀)