【LetMeFly】2583.二叉树中的第 K 大层和：层序遍历 + 排序

力扣题目链接：https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/

给你一棵二叉树的根节点 root 和一个正整数 k 。

树中的 层和 是指 同一层 上节点值的总和。

返回树中第 k 大的层和（不一定不同）。如果树少于 k 层，则返回 -1 。

注意，如果两个节点与根节点的距离相同，则认为它们在同一层。

 

示例 1：

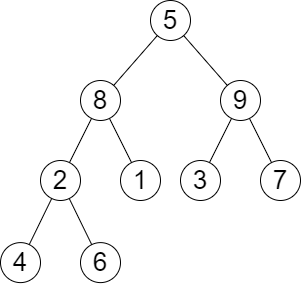
输入：root = [5,8,9,2,1,3,7,4,6], k = 2
输出：13
解释：树中每一层的层和分别是：
- Level 1: 5
- Level 2: 8 + 9 = 17
- Level 3: 2 + 1 + 3 + 7 = 13
- Level 4: 4 + 6 = 10
第 2 大的层和等于 13 。

示例 2：

输入：root = [1,2,null,3], k = 1
输出：3
解释：最大的层和是 3 。

 

提示：

• 树中的节点数为 n
• 2 <= n <= 105
• 1 <= Node.val <= 106
• 1 <= k <= n

方法一：层序遍历 + 排序

如果已经掌握了二叉树的层序遍历，那么这道题将会如鱼得水。

我们依然进行层序遍历，在层序遍历的过程中，计算每一层的节点值之和，并加入到一个数组中。

遍历结束后，对数组进行排序，返回第k大值或-1即可。

• 时间复杂度$O(N1+N2\log N2)$，其中$N1$是二叉树节点个数，$N2$是二叉树深度
• 空间复杂度$O(N3+N2)$，其中$N3$是最多一层的节点个数

时空复杂度也可以将全部的$N$都视为二叉树节点个数。

AC代码

C++

typedef long long ll;
class Solution {
public:
    ll kthLargestLevelSum(TreeNode* root, int k) {
        vector<ll> values;
        queue<TreeNode*> q;
        q.push(root);
        while (q.size()) {
            ll cnt = 0;
            for (int _ = q.size(); _ > 0; _--) {
                TreeNode* thisNode = q.front();
                q.pop();
                cnt += thisNode->val;
                if (thisNode->left) {
                    q.push(thisNode->left);
                }
                if (thisNode->right) {
                    q.push(thisNode->right);
                }
            }
            values.push_back(cnt);
        }
        sort(values.begin(), values.end());
        return k > values.size() ? -1 : values[values.size() - k];
    }
};

Python

注意本题数据级别是$10^5$，不能使用数组切片模拟队列的方式。

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthLargestLevelSum(self, root: TreeNode, k: int) -> int:
        values = []
        q = [root]
        while q:
            cnt = 0
            thisLayer = q
            q = []
            for thisNode in thisLayer:
                cnt += thisNode.val
                if thisNode.left:
                    q.append(thisNode.left)
                if thisNode.right:
                    q.append(thisNode.right)
            values.append(cnt)
        values.sort()
        return values[len(values) - k] if len(values) >= k else -1

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136252010