洛谷 P9221 「TAOI-1」Pentiment

题解区说这题同类型，先码住，有时间做一下。

---

思路：

这题是个动态规划，如何动规在洛谷题解区第一篇题解中讲的非常详细了，不赘述了。

这里主要考虑如何快速实现求解，假设现在第 $i-1$ 行的 $dp$ 值已经算出来了了，现在要算第 $i$ 行的 $dp$ 值，先不看第 $i$ 行上的障碍，那么形状差不多像下面：

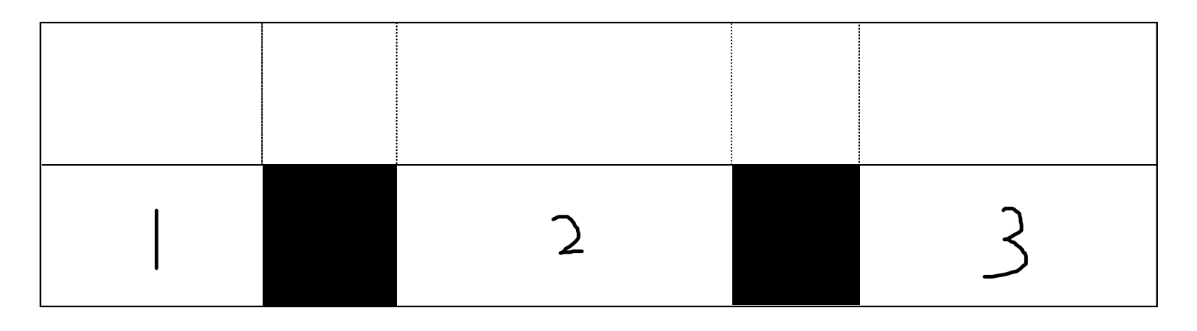
假设第一，二行就是第 $i$，$i-1$ 行。那么第 $i$ 行的区间 $1$ 上的每个位置都相当于第 $i-1$ 行的区间 $1$ 中的元素之和（也就是区间长度乘以一个元素值），同理其他对应的区间。障碍上面位置答案值就是0。现在加入障碍：

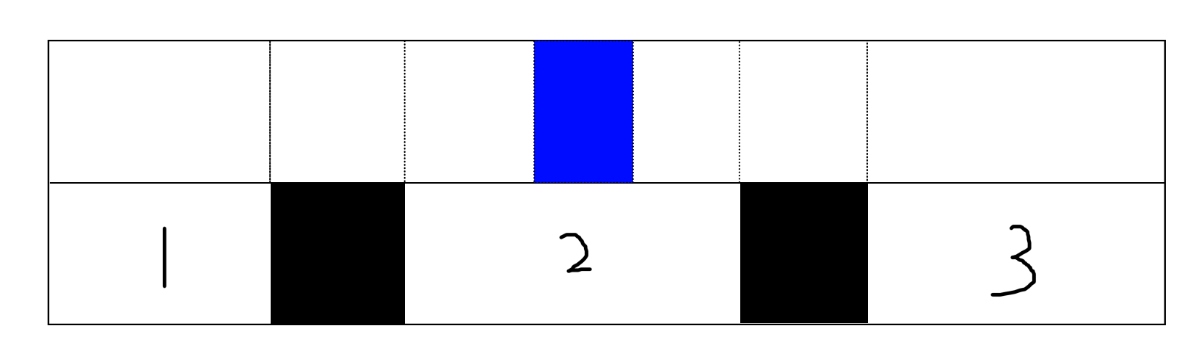
放入障碍的地方答案被清零。其他地方的答案值不变。

这样递推的过程就分析结束了。考虑到区间长度可能会很大，但是区间个数本身很小，因此考虑将每个区间压成一个点，这就和珂朵莉树的思想相似了。尝试用珂朵莉树维护一行的信息。

一开始有区间123以及两个障碍点，如果我们对第 $i$ 行边界到蓝色障碍这一块去找珂朵莉树中的区间12并计算答案之和会很麻烦，而且也不能使用split对区间进行拆开。求和之后也不能覆盖到珂朵莉树中。

考虑到我们可以先把答案算出来，然后再放入障碍。假设我们算出了第 $i-1$ 行区间1，2，3分别的区间和并保存在珂朵莉树中，这就相当于算出了第 $i$ 行中对应区间1，2，3上的每个元素值。现在直接加入蓝色障碍，并对前一个障碍或边界到加入的蓝色障碍这一段区间进行求和并用assign函数把它缩成一个点，这样得到的就是第 $i$ 行这一段上的区间和。算出所有的区间和后。问题就又回到了开头——我们算出了第 $i$ 行的每段区间的区间和，问第 $i+1$ 行的每段的区间和。

但是这样还是会超时，因为 $n$ 太大了，而 $q$ 相对来说就很小。因此会出现很多空行，考虑对空行进行合并，发现如果经过了 $k$ 个空行，其实就相当于对整段上的区间和乘以 $m^{k-1}$。所以在枚举第 $col$ 行的障碍时，如果发现障碍在第 $s$ 行，那么中间会经过 $s-col$ 个空行，区间和乘上 $m^{s-col-1}$ 即可。或者后面没有障碍了，直接到第 $n$ 行会有 $n-col+1$ 个空行，区间和乘上 $m^{n-col}$。

颜色段均摊是一种思想，说白了就是把一段性质相同的区间压成一个点。这个广义的颜色段其实就是具有某一性质的一段区间。实现颜色段均摊的思想用珂朵莉树相当合适。因为珂朵莉树就是把值相同的区间合并成一个结点保存在 set 里面。

code：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <set>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll mod=998244353;

ll n,m,q;

ll qpow(ll a,ll b){
	ll base=a%mod,ans=1;
	while(b){
		if(b&1){
			ans*=base;
			ans%=mod;
		}
		base*=base;
		base%=mod;
		b>>=1;
	}
	return ans;
}

struct ODT{
	#define SIT set<Node>::iterator
	
	struct Node{
		int l,r;
		mutable ll val;
		Node(int l,int r=0,ll val=0):l(l),r(r),val(val){};
		bool operator<(const Node x)const{return l<x.l;}
	};
	set<Node> s;
	
	void print(){
		for(auto x:s)printf("[%d,%d] %lld\n",x.l,x.r,x.val);
		printf("\n");
	}
	void build(int n){
		s.insert(Node(1,n,1));
		s.insert(Node(n+1,n+1,0));
	}
	SIT split(int pos){
		SIT it=s.lower_bound(pos);
		if(it!=s.end() && it->l==pos)return it;
		it--;
		int l=it->l,r=it->r;
		ll val=it->val;
		s.erase(it);
		s.insert(Node(l,pos-1,val));
		return s.insert(Node(pos,r,val)).first;
	}
	SIT assign(int l,int r,ll v){
		SIT it2=split(r+1),it1=split(l);
		s.erase(it1,it2);
		return s.insert(Node(l,r,v)).first;
	}
	ll query(int l,int r){
		SIT it2=split(r+1),it1=split(l);
		ll ans=0;
		for(;it1!=it2;it1++)
			ans=(ans+(it1->r-it1->l+1)*it1->val%mod)%mod;
		return ans;
	}
	
	#undef SIT
}tr;

pair<ll,ll> bar[maxn];

int main(){
	cin>>n>>m>>q;
	for(int i=1;i<=q;i++)cin>>bar[i].first>>bar[i].second;
	tr.build(m);
	for(int p=1,col=1,l;col<=n;col++){
		if(p>q){
			ll line=n-col;
			tr.assign(1,m,tr.query(1,m)*qpow(m,line)%mod);
			break;
		}
		if(bar[p].first>col){
			ll line=bar[p].first-col-1;
			tr.assign(1,m,tr.query(1,m)*qpow(m,line)%mod);
			col=bar[p].first;
		}
		
		l=1;
		while(bar[p].first==col){
			int r=bar[p].second;
			if(l<r){
				tr.assign(l,r-1,tr.query(l,r-1));
			}
			tr.assign(r,r,0);
			l=r+1;
			p++;
		}
		if(l<=m){
			tr.assign(l,m,tr.query(l,m));
			l=m+1;
		}
	}
	cout<<tr.query(1,m)<<endl;
	
	return 0;
}