题目

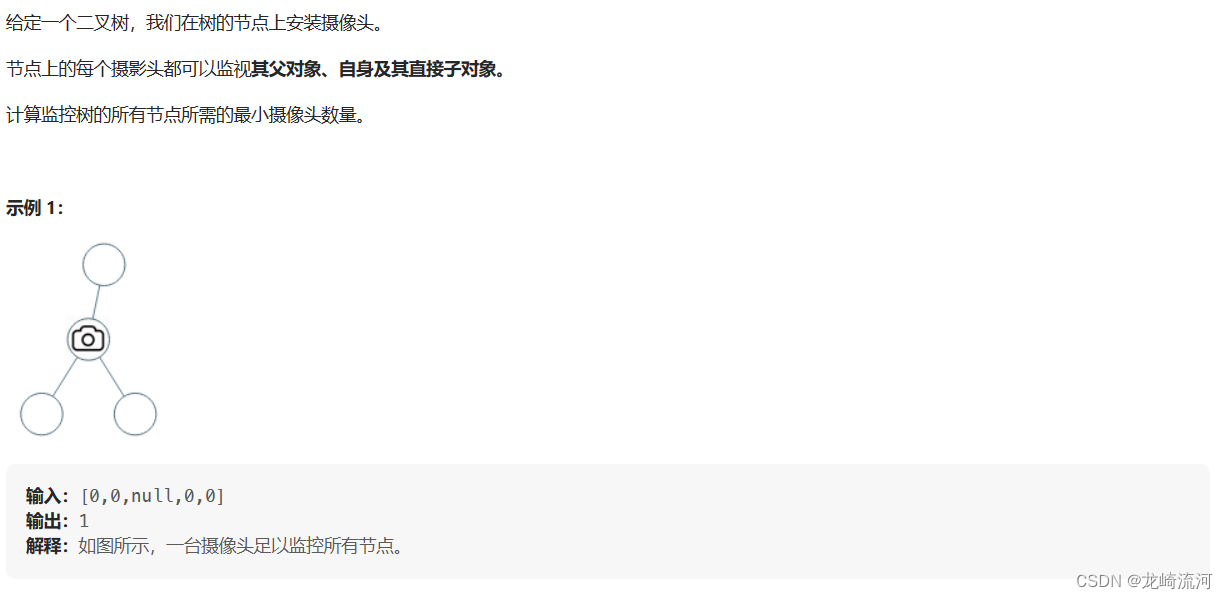
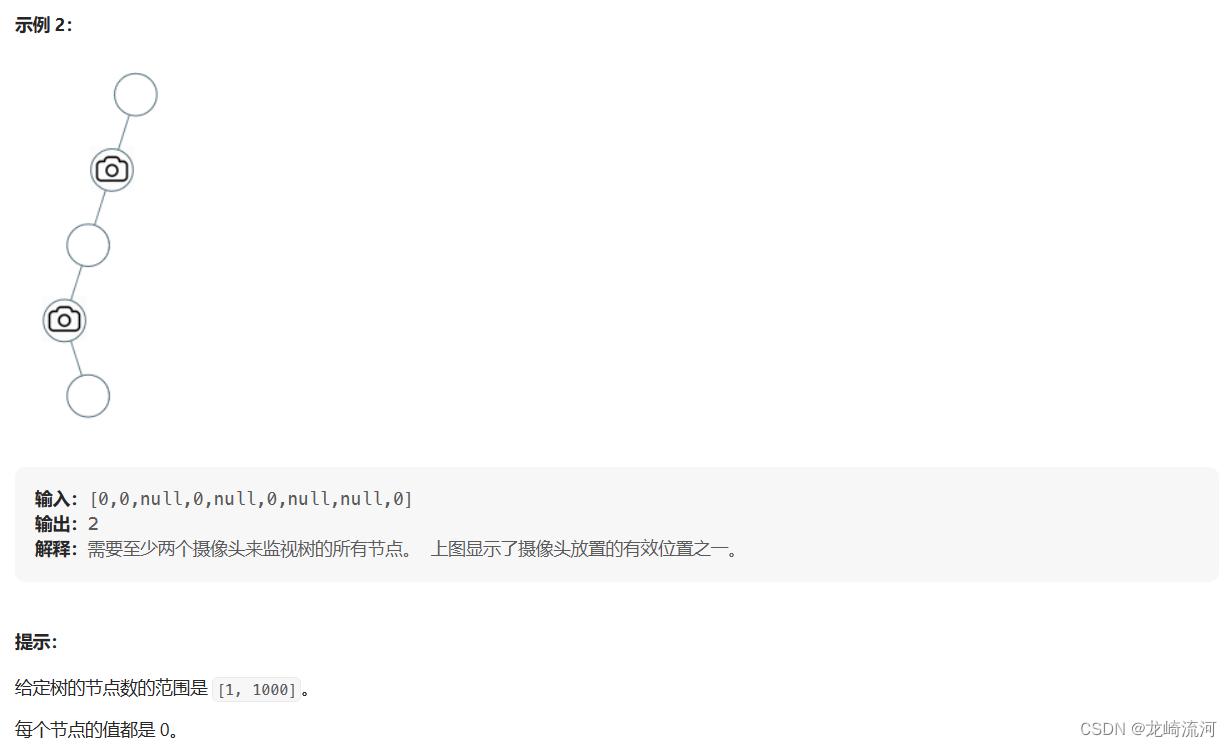
分析

首先明确把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。
贪心算法：
从下到上看局部最优，因为下面的节点最多，让叶子节点的父节点安摄像头最合理，所用摄像头最少。
整体全局最优，全部摄像头数量最少。
采用后序遍历能做到从下到上遍历。
来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

• 0：该节点无覆盖
• 1：本节点有摄像头
• 2：本节点有覆盖

判断空节点状态：
空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了。
四种情况：

• 左右节点都有覆盖，中间节点就是无覆盖状态：
  
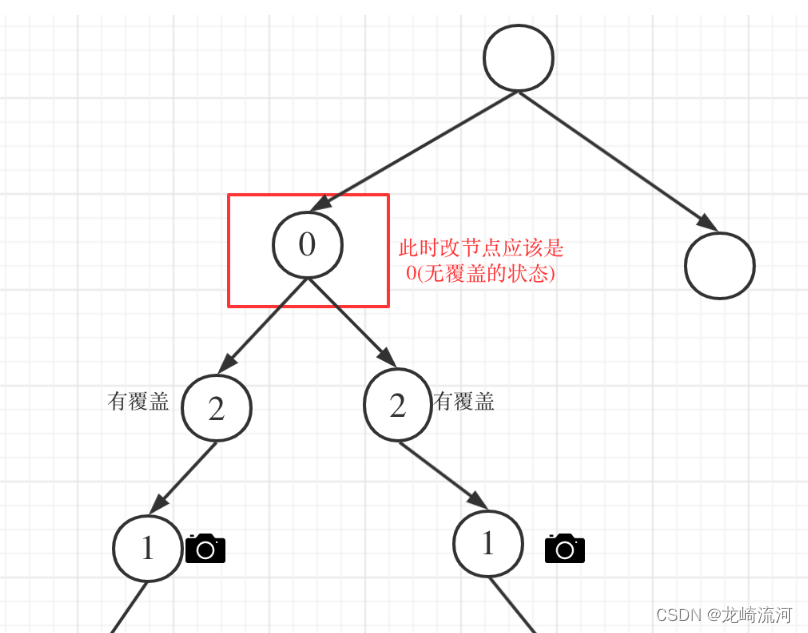
• 左右节点至少有一个无覆盖的情况：

left == 0 && right == 0 左右节点无覆盖 ，
left == 1 && right == 0 左节点有摄像头，
右节点无覆盖 left == 0 && right == 1 左节点有无覆盖，
右节点摄像头 left == 0 && right == 2 左节点无覆盖，
右节点覆盖 left == 2 && right == 0 左节点覆盖，右节点无覆盖

这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。
此时摄像头的数量要加一，并且return 1，代表中间节点放摄像头。

• 左右节点至少有一个有摄像头：
  如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

left == 1 && right == 2 左节点有摄像头，
右节点有覆盖 left == 2 && right == 1 左节点有覆盖，
右节点有摄像头 left == 1 && right == 1 左右节点都有摄像头

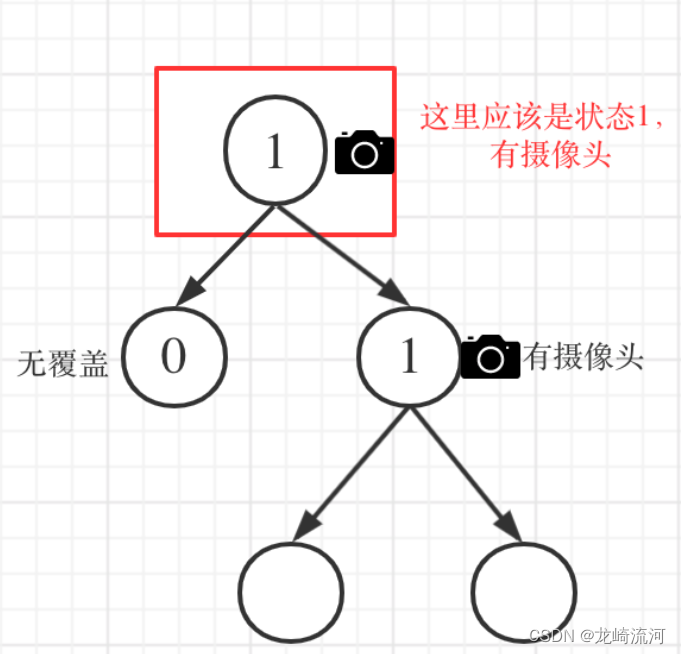
• 头结点没有覆盖
  最后判断下头节点是否为0，如果为0则将其变成摄像头。
  

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int nums = 0;
    public int minCameraCover(TreeNode root) {
        if(minCame(root) == 0){
            nums++;
        }
        return nums;
    }
    public int minCame(TreeNode root){
        if(root == null) return 2;
        int left = minCame(root.left);
        int right = minCame(root.right);
        if(left == 2 && right == 2){
            return 0;
        }else if(left == 0 || right == 0){
            nums++;
            return 1;
        }else{
            return 2;
        }
    }
}