倒计时49天！

前缀和的拓展——压缩矩阵

最大子段和

7
2 -4 3 -1 2 -4 3

4

题目分析

提供一下类似动态规划的解法，而这个动态规划dp数组的定义类似最长上升子序列里面dp数组的定义。

第一阶段定义dp数组

直接定义dp数组。dp[i]表示以第i个字母结尾的最大字段和。

第二阶段推导状态转移方程

对于dp[i]我可以从两个地方转移过来，即以a[i-1]结尾的最大子段和加上a[i]和a[i]自己，那么从这两个转移状态里面选一个最大的就可以了，状态转移方程是下面的式子。

$dp[i]=max(dp[i-1]+a[i],a[i])$

第三阶段写代码

（1）dp数组初始化。这里求的是最大值，一般初始状态是为0，但是这里可能会出现负数的情况，要初始化为较小值吗？不需要，我们可以看一下$dp[1]=max(dp[0]+a[1],a[1])$，这里的dp[0]=0是对的，因为对于前0个数字，它的和就是0。每次dp[i]都会可能的值被更新，而dp[i+1]只用到了dp[i]。所以不用初始化。写的有点啰嗦了。

（2）递推dp数组。这里只需要遍历一次a数组就行了。

（3）答案。min(dp[i])。

题目代码

import java.util.Scanner;
public class Main {
public static void main(String[] args) {
	Scanner scanner=new Scanner(System.in);
	int n = scanner.nextInt();
	int a[] = new int[n+1];
	int dp[] = new int[n+1];
	int ans = Integer.MIN_VALUE;
	for(int i = 1;i <= n;i++) {
		a[i] = scanner.nextInt();
		dp[i] = Math.max(dp[i-1]+a[i], a[i]);
		ans = Math.max(dp[i], ans);
	}
	System.out.println(ans);
}
}

最大加权矩形

 0 –2 –7  0 
 9  2 –6  2
-4  1 –4  1 
-1  8  0 –2

9  2
-4  1
-1  8

4
0 -2 -7 0
 9 2 -6 2
-4 1 -4  1 
-1 8  0 -2

15

题目分析

这道题是最大子段和的二维形式。可尝试把它压缩成一维。我们利用前缀和对矩阵进行行压缩。行压缩的结果是$a[i][j]$里面存的是前i行第j列的和，其实就是相对于第j列的前缀和。假设$a[i][j]$初始值是矩阵的值，那么类比于$sum[i]=sum[i-1]+a[i]$的前缀和求解方法，可以利用下式求前缀和，
$$a[i][j]+=a[i-1][j]$$
求完前缀和后，如果我要求第j列，第l行到第r行的和，用$a[r][j]-a[l-1][j]$表示。如果我要求以i行结尾的矩阵的最大值，那么应该怎么求？如下图所示，

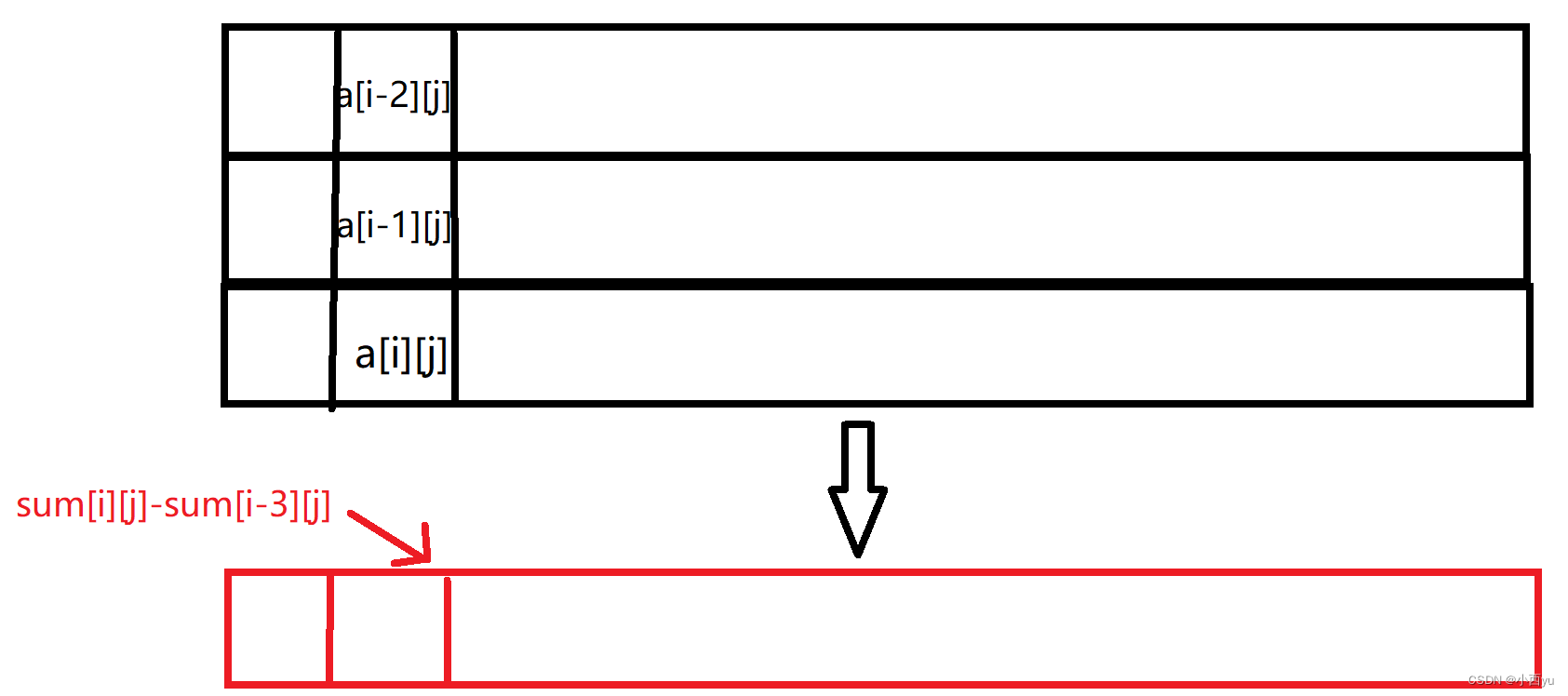
原本我求第j列某几行的和，我需要依次相加，但是压缩后，我只需要用一个式子一下子就可以表示出来第j列某几行的和，现在相当于把矩阵压缩成了一维的形式，我只需要移动j就可以了。定义两个数组f[j]和dp[j]，dp[j]的含义和最大子段和的含义一样，在行固定的情况下以第j列结尾的最大矩阵和，那么它的转移也和最大子段和一样，f[j]就表示在行固定的情况下第j列的矩阵和，它相当于最大子段和里面的a[i]。

对应的关键代码如下，

for(int i = 1;i <= n;i++) {
		for(int k = 1; k <= i;k++) {
			int f[] = new int[n+1];
			int dp[] = new int[n+1];
			for(int j = 1;j <= n;j++) {
				f[j] = a[i][j]-a[i-k][j];
				dp[j] = Math.max(dp[j-1]+f[j], f[j]);
				ans = Math.max(dp[j], ans);
			}
		}
	}

要想固定行，最低行和最高行都要固定，所以两层for循环是不可少的，固定了行之后再遍历列就可以了。

题目代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Scanner;

public class Main {
public static void main(String[] args) throws IOException {
	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	Scanner scanner = new Scanner(System.in);
	int n = scanner.nextInt();
	int a[][] = new int[n+1][n+1];
	for(int i = 1;i <= n;i++){
		int id = 1;
		for(int j = 1;j <= n;j++) {
			a[i][j] = scanner.nextInt();
			a[i][j] += a[i-1][j];//利用前缀和进行矩阵的行压缩
		}
	}
	long ans = 0;
	for(int i = 1;i <= n;i++) {
		for(int k = 1; k <= i;k++) {
			int f[] = new int[n+1];
			int dp[] = new int[n+1];
			for(int j = 1;j <= n;j++) {
				f[j] = a[i][j]-a[i-k][j];
				dp[j] = Math.max(dp[j-1]+f[j], f[j]);
				ans = Math.max(dp[j], ans);
			}
		}
	}
	System.out.println(ans);
}
}