l) 时域相位分析技术 在光 学测量 的许 多情况 下 , 时变图像信 号 的背景光 强 与调制 度可 以看作是 常 数 ,并且 其光 强 随时 间 的变化也满足 正 弦条件 。 那 么针 对某 一 空 间采样 点 (x ,y) , 某时刻 采 集到 的光 强 可 以表 示 为:
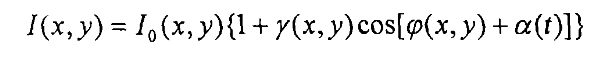

-
三步法(Three-step method):
- 采集三幅相移条纹图像,相移量取3个不同的数值。这种方法采集图像数量少,处理速度快,但不能有效抑制相移误差对检测精度的影响。
-
Carré法(Carré method):
- 不需要对相移量进行校准,对相移误差敏感,但线性误差不敏感。这种方法能有效抑制探测器的二次非线性响应。
-
四步法(Four-step method):
- 能有效地抑制探测器的二次非线性响应,对相移误差的影响较小,但采集图像数量相对较多。
-
五步法(Five-step method):
- 相比四步法,能抑制包括背景调制在内的多种误差,但采集的图像数量更多,计算量相对较大。
-
最小二乘法(Least Squares Method):
- 有效抑制包括背景调制与图像信噪比在内的误差,特别是对于呈正态分布的随机误差。
-
迭代最小二乘法(Iterative Least Squares Method):
- 提出了一种基于最小二乘的迭代算法,用于求解相移量,能够提供更精确的相位数据。
ll) 空域相位测量技术试图从单幅条纹图中获取相位数据,因而更适合于动态的三维测量。常见的方法有傅里叶变换法(Fourier Transform Method,FTM)l1,21,空间相移法(Spatial Phase-shifting Method,SPSM)[33-38],卷积解调法[39.40],等等,
-
傅里叶变换法(Fourier Transform Method):
- 通过在干涉条纹图像上应用傅里叶变换,将条纹频谱与背景频谱分离,从而提取出相位信息。这种方法适用于动态三维测量,因为它仅需要单幅条纹图像

- 通过在干涉条纹图像上应用傅里叶变换,将条纹频谱与背景频谱分离,从而提取出相位信息。这种方法适用于动态三维测量,因为它仅需要单幅条纹图像
-
空间相移法(Spatial Phase-shifting Method):
- 在这种方法中,通过在空间上移动参考镜来引入人为的空间载波,然后对多个相移后的条纹图像进行处理,以求解相位。
-
卷积解调法(Convolution Decoding Method):
- 利用卷积定理,将条纹图像与已知的参考波形进行卷积,以分离出相位信息。
-
小波变换(Wavelet Transform):
- 小波变换是一种多分辨率分析方法,可以用来处理非平稳信号。在三维测量中,小波变换可以用来分析和提取条纹图像中的相位信息。
-
迭代的最小二乘相移算法(Iterative Least Square Phase-shifting Algorithm):
- 这种方法结合了时域和空域的相位分析技术,通过迭代过程来优化相位解包裹的结果。
-
短时傅里叶变换(Short-Time Fourier Transform, STFT):
- 也称为加窗傅里叶变换,它通过在信号上滑动一个固定大小的窗口,然后对窗口内的信号进行傅里叶变换,以分析信号在不同时间点的频率成分。
-
连续小波变换(Continuous Wavelet Transform, CWT):
- 与STFT类似,CWT使用可变大小的窗口来适应信号的局部特性,适用于分析具有不同频率成分的信号。