知乎同名账号同步发表

无/自监督去噪(1)——一个变迁：N2N→N2V→HQ-SSL

读前须知

注意：本文不含$L_0$ loss的理论分析及相关实验，仅对N2N原文部分实验进行解析，主要从数学角度分析N2N为什么能work。

1. 前置知识——L1和L2 loss的特性

此处参考https://www.cnblogs.com/wangguchangqing/p/12021638.html

此部分仅讲述特性。$L_2$ loss或者叫均方误差（MSE），简单来说就是预测值和GT之间差值的平方的均值。MSE的特点是曲线光滑、连续、处处可导。MSE对离群点比较敏感，如果样本中存在离群点，则会给离群点更高的权重，这样会牺牲正常点数据的预测结果，降低总体性能。当离极小值较远的时候，梯度也比较大，好处是初期可能因此收敛快，坏处是可能遭遇梯度爆炸的情况。

至于$L_1$ loss，或者叫均绝对误差（MAE），是预测值和GT之间差值的绝对值的均值。MAE曲线在极小值处不可导，同时在大部分情况下梯度都是相等的，这意味着对于很小的损失值（此时需要慢点下降）梯度显得大，而对于很大的损失值（此时需要快速收敛）梯度显得小。也许这样不利于模型的收敛，但是梯度较为稳定，不会导致梯度爆炸问题，而且具有较为稳健的解。正因为损失很大时梯度也保持和小损失时的一致，所以MAE对离群点不是太敏感。

⭐️为了便于理解，我在此举例：如果我们给了一堆数据点，并以它拟合了一条直线。大部分数据点都在直线上或者直线附近，但是存在极少量数据点距离直线较远，明显偏离了直线所能描述的情况。这种极少数的点我们称之为离群点。进一步，我给一个定义叫：离群性，它能够描述一个点的离群程度。表现在这个例子上即为距离直线越远的数据点，离群性越高。

⭐️均值和中位数是两种不同的概念，在本文中，我采用一个新颖的观点描述它们的区别：离群性是均值和中位数区别的来源。假设有一个样本集合，其中90%的值都是145~155，只有10%的值为0~10，我们姑且可以认为在0~10之间的值表示离群点，它们的离群性较高。显然，它们的中位数将会是145~150之间，也许就刚好是150，进一步，如果样本集合中没有10%的离群点，中位数的结果似乎不会有太大的影响，就仿佛在求解中位数时，离群点被“忽略”了一样；然而，它们的均值会受到离群点较大的影响，也许会明显低于150，因为均值要充分考虑离群点，进一步，极端情况下如果那10%的数字范围在-1000000000左右，那么最终求得的均值将会远远偏离150这个数量级，此时均值将不能描述这个样本集的基本状况。由此，我们给出该角度下均值和中位数的根本区别：均值是充分考虑到离群点的统计量，考虑的是全面；中位数是适当舍弃离群点的统计量，考虑的是大局

⭐️给定一个样本，90%都是150，10%是0。当采用$L_2$ loss时，由于会考虑到所有样本点，预测值会低于150，向均值收敛；当采用$L_1$ loss时，由于可能会忽略离群点，预测值倾向于向150——也就是中位数收敛。

有了此部分补充，我们接下来仔细了解Noise2Noise的几个实验，以及它们对应的理论分析。（关于Noise2Noise的简单讲解，可以参考我之前的文章，或者自行搜索相关详解。读者需要格外注意$L_2$ loss和$L_1$ loss的区别，Noise2Noise针对不同的任务采用了不同的loss。简单回顾结论：用$L_2$ loss则向均值mean收敛，用$L_1$ loss则向中位数median收敛）

2. additive Gaussian noise (spatial independent noise), $L_2$首杀

满足噪声零均值假设，故而此项实验采用$L_2$ loss，根据前文分析，这会使得网络输出的每个像素收敛到mean——也就是$E(信号+噪声)=信号+E(噪声)=信号$

数据集为$256\times 256$的patches，来自IMAGENET validation set的50k张图片。对于每个训练数据，随机添加标准差为$\sigma \in [0,50]$的加性高斯噪声。作者称这是盲去噪，因为magnitude(大小，数量级) of noise也是未知的。

通过实验，作者说明无论从效果还是收敛速度的角度，在加性高斯噪声去噪任务中，有监督学习都是没有必要的。不过需要注意加性高斯噪声在所有像素中都是独立同分布的(i.i.d.)，也就是说该项实验应对的是spatial independent noise

3. brown Gaussian noise (spatial dependent noise), $L_2$双杀

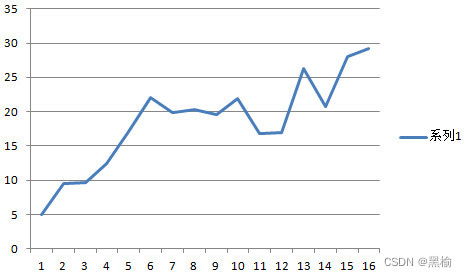
作者在加性高斯噪声的实验介绍部分，插入了brown Gaussian noise去噪任务的讲解。此项试验同样采用$L_2$ loss，但是在收敛速度上有所区别。

For brown Gaussian noise, we observe that increased inter-pixel noise correlation (wider spatial blur; one graph per bandwidth) slows convergence down

博主对brown Gaussian noise不太了解，该引用是论文原文内容，它的意思是：当增加了像素间的noise correlation时，网络的收敛速度会变慢。加性高斯噪声是spatial independent noise，brown Gaussian noise是spatial dependent noise。

⭐️通过一个例子讲讲我个人的理解——为什么增加inter-pixel noise correlation时，会造成网络的收敛速度变慢？假设现在有三个靶子，你需要用枪射击。每个靶子上有一个致命位置，但是你不知道在哪里。如果每次射击过后，我都会告诉你一个假的坐标，骗你这是该靶子的致命位置。N2N的思想就是如果我给的若干错误答案，其平均值是正确答案，那么你就能学会打靶。当增加inter-pixel noise correlation时，相当于增加这样的条件：如果你打第一个靶子偏左，那么第二个靶子一定会偏右。这样就破坏了随机性，仔细思考一下N2N的数学基础，其核心是噪声是随机的且均值为0。如果添加了inter-pixel noise correlation，噪声就倾向于变成一个结构信息，没准一张inter-pixel noise correlation足够强的noisy image，只保留noise的部分，你也能一眼看出有意义的内容。网络在学习的过程中，正是因为$随机噪声\to 随机噪声$这一$随机\to 随机$的映射无法学习，所以才会向mean收敛。然而，网络是有感受野的，因此结构信息（structural information）是可学习的。如果这个随机噪声在若干相邻像素组成的patch中表示了一种structural information，那么网络就会因此试图产生学习行为，这样方才提到的$随机\to 随机$这一映射，在少量feed forward+back propagation（单个epoch）中就很难被网络判定为不可学的。虽然inter-pixel correlated noise具备structural information，但不同epoch的noise，通过它们对应的structural information们并无法总结出统一的规律，仍旧具备随机性。所以，在经历了较大的epoch后，网络无法总结出大量epoch的structural information之间的规律，于是网络才会逐渐判定$随机噪声\to 随机噪声$这一映射无法学习，便会向mean收敛。

综上，添加inter-pixel noise correlation时，或者noise拥有more spatial dependent时，网络需要更多的epoch来确认$随机噪声\to 随机噪声$这一映射无法学习，“认识到”向mean收敛才是光明大道。总之当变成spatial dependent noise时，收敛速度会变慢，这些是有些文章(比如SA-SSID, 2023 CVPR)将N2N归类为只能处理spatial independent noise的算法的原因。不过根据原文来看，最终效果还可以，较为接近有监督学习，即便是extreme blur的情况。

⭐️此实验说明N2N可以应对spatial dependent noise，即包含inter-pixel noise correlation的情况，只是收敛速度相较于spatial independent noise更慢。

4. blind text removal, $L_2$导致结果偏灰, $L_1$前来破局

该项实验采用$L_1$ loss，根据前文分析，网络输出的像素点倾向于收敛到中位数。

我们先简单介绍该项实验的概况：

将大量随机颜色的文字添加到图片上，对图片原本的内容形成一定的遮盖。这些文字的方向和字体保持不变。需注意这些文字的颜色和位置都是随机的，而且和图像原本的signal pixel没有关联。该任务的目标就是将随机添加的文字都从图片中去除掉，理想的输出是原始的图片。注意所添加的文字数量是有限的，在训练阶段$p$在$[0,0.5]$之间，p表示每个像素被遮盖的概率；在测试阶段$p$大约是$0.25$。

在继续之前，我们先看一下中灰色，因为它和理解作者原文描述密切相关。网上搜索了一个中灰色的色号：

GSB05-1426-2001 72 B02色号的RGB色值为(114,123,124)

可以以此判断RGB均在0~255的平均值，颜色的视觉效果就是中灰色。接下来我们看原文中的一段话：

In this test the mean (L2 loss) is not the correct answer because the overlaid text has colors unrelated to the actual image, and the resulting image would incorrectly tend towards a linear combination of the right answer and the average text color (medium gray).

原作者的意思是这里的mean不代表correct answer，因为所添加的大量随机颜色的文字，经过叠加之后的平均值应该是中灰色这一RGB为0~255平均值的颜色。也就是说根据Noise2Noise的理论，如果在这里直接用$L_2$ loss进行训练，会导致像素被还原为中灰色，而不是signal pixel。

不过，我们可以考虑用$L_1$ loss，因为$p$ (每个像素被遮盖的概率)的值在$[0,0.5]$这个范围，意味着一个像素点没有被遮盖的概率更大一些。此时样本的中位数倾向于为原始图像信号，而非添加的文字像素。我们可以视添加的文字像素点具备一定的离群性（此概念详见前文），而$L_1$的作用就是抑制具备离群性的数据，推动网络还原出原始图像信号。摘录一段作者原文如下：

However, with any reasonable amount of overlaid text, a pixel retains the original color more often than not, and therefore the median is the correctstatistic.

在该任务中，mean不能代表正确的图像信号，所以不能用$L_2$ loss促进网络向预测出mean收敛，但是median（中位数）恰恰是正确的统计量，所以采用$L_{1}loss$促进网络向预测出median收敛。通过实验结果，可以发现$L_2$ loss效果比较差，$L_1$ loss更佳：

5(选读). ——random-valued impulse noise, 使用$L_0$的情况(无理论分析)

论文原文有Dirac（狄拉克）字样，此处附上狄拉克分布资料：https://blog.csdn.net/hy592070616/article/details/120605471

对于图像中每个像素点，依概率p将该像素点替换为一个color，该color采样自一个均匀分布$[0,1{]}^3$；依概率1-p将该像素点维持原样。类似于章节4，$L_2$在此实验中不可用，会导致结果向中灰色偏移；与章节4不同，此处没有限制p小于0.5，所以median可能不是正确答案（但是p小于0.5时实验结果不错，作者在原论文中提到了这一点；大于这个阈值则会导致bright和dark向灰色偏移）。故而不能采用$L_1$或者$L_2$ loss进行解答。

作者采用的是annealed version of $L_0$ loss，定义如下：
$$(|f_{\theta }(x)-y|+ϵ{)}^{\gamma },$$
其中$ϵ=10^{-8}$，$\gamma$在训练期间从2到0线性衰退。

在训练时，p随机从$[0,0.95]$采样。可以看到p可能是一个远大于0.5的值，所以此时如果强行使用$L_1$ loss，如果碰巧p小于0.5（此时median是正确答案），作者发现会获得一个不错的结果；如果大于0.5这个阈值，作者发现图像中bright或者dark的区域会向gray偏移。如果采用$L_2$ loss，作者发现结果会严重向gray偏移，这是因为此时mean是correct answer+mean of uniform random corruption（在章节4中，我们描述过RGB均在平均值的颜色是中灰色，这意味着此处每个像素都会在原来的基础上叠加一个中灰色）。当作者采用$L_0$ loss时，几乎没有偏移，即便是p到达90%（很严重的corruption）。此处作者在原文有相关描述：

$L_0$, on the other hand, shows little bias even with extreme corruptions (e.g. 90% pixels), because of all the possible pixel values, the correct answer (e.g. 10%) is still the most common.

（总之在作者的实验中，如果平均数和中位数都不是正确答案时，作者尝试采用了L0 loss，获得了不错的结果。L0 loss的原理博主不太了解，为什么它能够解决L1和L2都不能解决的问题呢？如果读者有相关资料，欢迎在评论区补充。）

不同loss对应的实验结果如下：

可以看到不同的loss会带来不同的效果。本文呈现了N2N中多个loss对结果的不同影响，并通过对部分loss的特性分析，理解了造成这种不同的原因。Noise2Noise是无监督领域的经典大作，它巧用数学为无监督学习打开了一扇大门，欢迎有兴趣的朋友们评论区交流观点、指正本文的不足。

本账号关于无监督图像去噪系列的文章按原计划还有一期，此后将开始涉足AIGC、后端开发等领域，欢迎且感谢交流、关注、批评。