互联网的大龄焦虑
今天看到一个老生常谈的话题「大龄焦虑:都市容不下躯壳,老家容不下灵魂」。
现如今,内卷已不是互联网行业专属名称,早已渗透到一线城市中的各行各业。
但地域落差对职业的影响,互联网行业还是稳稳的位于第一梯队。
一些出生在相对落后省份的同学,回老家意味着失业换行。
某些城镇可能根本没有匹配程序员的岗位,而在一线城市,程序员又是碗"青春饭"。
近两年的毕业生人生屡创新高,不少同学是因为当时选专业的时候,未能突破原生家庭及周边环境的信息差,单纯因为听说「计算机行业工资高」选中当前专业。
入行了才知道「35 岁无人要」等黑话,于是转念一想,又从新把希望寄托于「像前几年毕业的小伙伴那样,在一线城市卷几年,等到年纪大的时候也就存够钱,到时再回老家」这样的计划。
但随着这几年互联网的急转直下,再结合一线城市房租的稳步上升,计划又一次败给了现实变化。
一位网友说出了自己的情况:
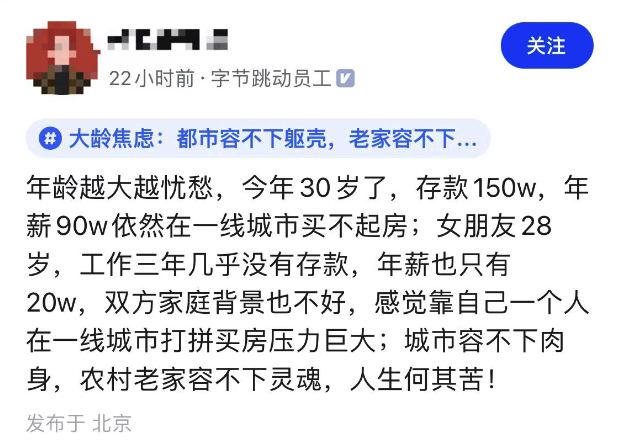
这位就职于「字节跳动」的同学已年到 30,存款 150W,伴侣存款不多,双方也都是普通家庭,对前途感到十分迷茫。
150W,如果是想在一线城市买房,再凑凑或许能在较远地区交个首付,但月供会成为大问题,贷款年限可能远比职业生涯要长 ...
150W,如果是回老家,肯定不是一笔小钱,但也不足以完全躺平 ...
这可是字节跳动,宇宙厂尚且如此。
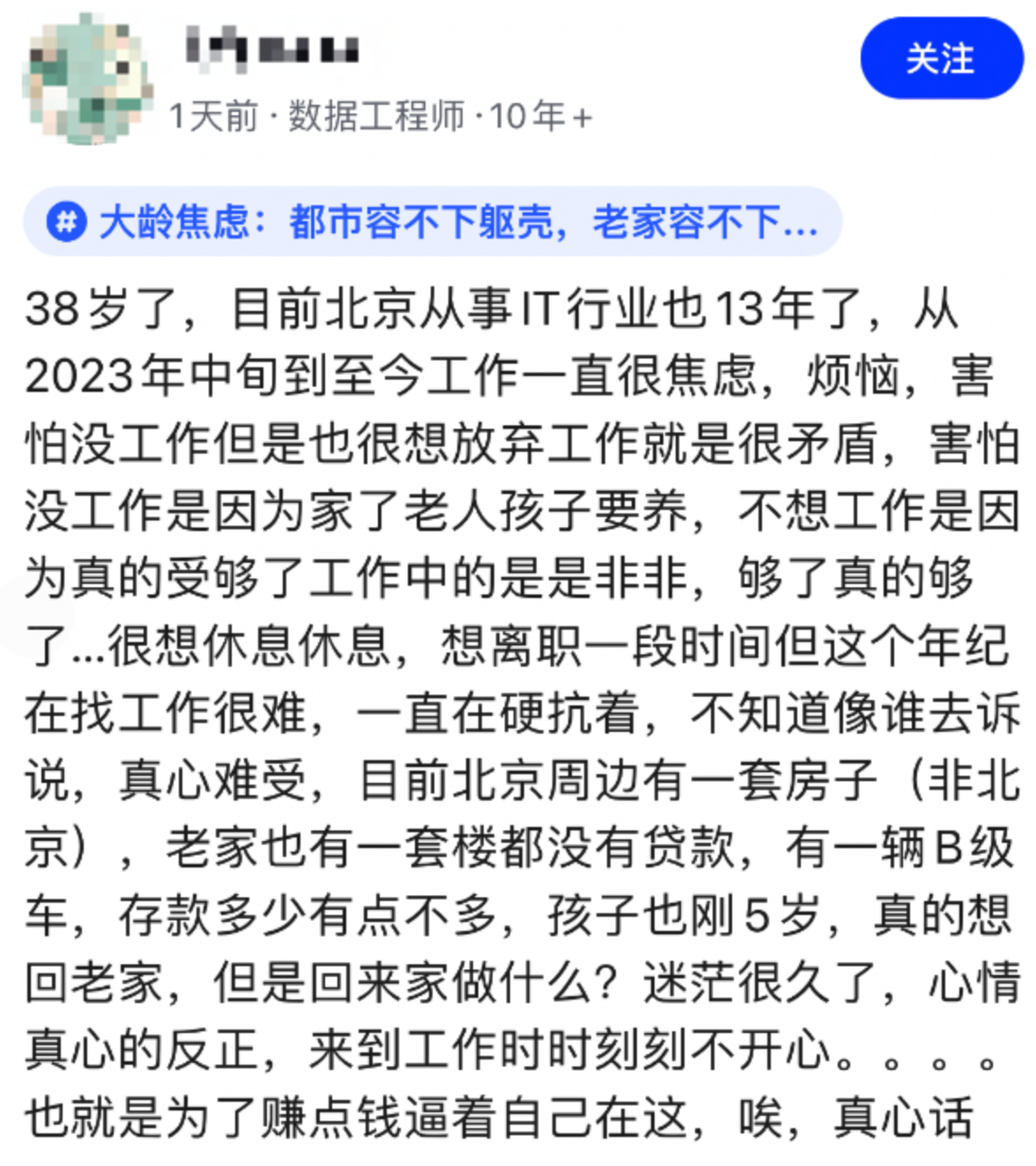
其他年龄更大的,或待遇更低的一线互联网从业者更是没有破局之路。

...
回归主线。
来一道最近网友们问得最多的,华为 OD 一面算法原题,题面略有修改(本题面剔除掉了故事背景,更裸),解法和代码完全一致。
现在华为 OD 都考 Hard 了,也是够卷的。
题目描述
平台:LeetCode
题号:891
一个序列的「宽度」定义为该序列中最大元素和最小元素的差值。
给你一个整数数组 nums,返回 nums 的所有非空子序列的宽度之和。
由于答案可能非常大,请返回对 取余后的结果。
子序列定义为从一个数组里删除一些(或者不删除)元素,但不改变剩下元素的顺序得到的数组。
例如,[3,6,2,7] 就是数组 [0,3,1,6,2,2,7] 的一个子序列。
示例 1:
输入:nums = [2,1,3]
输出:6
解释:子序列为 [1], [2], [3], [2,1], [2,3], [1,3], [2,1,3] 。
相应的宽度是 0, 0, 0, 1, 1, 2, 2 。
宽度之和是 6 。
示例 2:
输入:nums = [2]
输出:0
提示:
数学
提示一:每个子序列对答案的贡献
对于某个子序列而言,若其最大值为 ,最小值为 ,则该子序列对答案的贡献为 。
我们有若干个子序列,即有若干个
,答案为所有
之和,我们称一个
为 item。
提示二:每个
参与了多少个 item 的组成,在最终展开式中又是如何
对于每个
而言,a 和 b 均必然是具体的
。
同时易知若 作为了 个子序列的最小值,那么在最终表达式展开中,必然有 个 ;同理若 作为了 个子序列的最大值,那么在最终表达式展开中,必然有 个 。
提示三:统计每个 作为最值时,有多少个子序列
先不考虑 的重复问题。
若 作为子序列最小值时,首先 必选,小于 的必不选,而大于 的可选可不选,组合个数取决于大于 的数的个数,假设有 个,那么根据组合数原理,共有 个组合,即共有 个子序列。此时 对答案的贡献为 。
同理, 作为子序列最大值时,子序列个数取决于小于 的数的个数,假设有 个,此时 对答案的贡献为 。
提示四:如何快速得知比 大/小 的数的个数
排序。
提示五: 的重复问题
无论是将 视作最大值还是最小值,我们的组合数均取决于某一侧的数的个数,因此不会答案正确性产生影响。
提示六: 操作的重复计算问题
将 视作最值,我们都需要统计两边数所产生的组合数个数,因此即使对于单个用例都会面临重复计算某个 的问题(对称性)。
同时对于跨样例而言,我们仍会重复计算某些 (尤其是较小的 值),为避免重复计算,我们可以通过打表预处理的方式算得所有可能要用到 结果,在使用的时候直接通过查表取得。
Java 代码:
class Solution {
static int N = 100010, MOD = (int)1e9+7;
static long[] p = new long[N];
static {
p[0] = 1;
for (int i = 1; i < N; i++) p[i] = p[i - 1] * 2 % MOD;
}
public int sumSubseqWidths(int[] nums) {
int n = nums.length;
long ans = 0;
Arrays.sort(nums);
for (int i = 0; i < n; i++) {
ans += (p[i] * nums[i]) % MOD;
ans %= MOD;
ans -= (p[n - i - 1] * nums[i]) % MOD;
ans %= MOD;
}
return (int) ans;
}
}
TypeScript 代码:
function sumSubseqWidths(nums: number[]): number {
let n = nums.length, mod = 1000000007, ans = 0
const p = new Array<number>(n + 10).fill(1)
for (let i = 1; i <= n; i++) p[i] = p[i - 1] * 2 % mod
nums.sort((a,b)=>a-b)
for (let i = 0; i < n; i++) {
ans += p[i] * nums[i] % mod
ans %= mod
ans -= p[n - i - 1] * nums[i] % mod
ans %= mod
}
return ans
}
Python3 代码:
class Solution:
def sumSubseqWidths(self, nums: List[int]) -> int:
n, mod, ans = len(nums), 1000000007, 0
p = [1] * (n + 10)
for i in range(1, n + 1):
p[i] = p[i - 1] * 2 % mod
nums.sort()
for i in range(n):
ans = ans + p[i] * nums[i] % mod
ans = ans - p[n - i - 1] * nums[i] % mod
return ans % mod
-
时间复杂度:排序复杂度为 ;统计答案复杂度为 。整体复杂度为 -
空间复杂度:
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉