参考资料：https://zhuanlan.zhihu.com/p/273595649

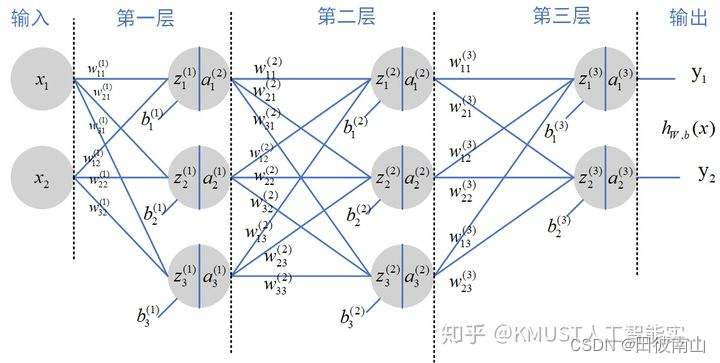
一、前向传播

1、第一层

（1）线性层

$$\{\begin{array}{c}{z}_1^{(1)}=w_{11}^{(1)}\ast x_1+w_{12}^{(1)}\ast x_2+b_1^{(1)}\\ z_2^{(1)}=w_{21}^{(1)}\ast x_1+w_{22}^{(1)}\ast x_2+b_2^{(1)}\\ z_3^{(1)}=w_{31}^{(1)}\ast x_1+w_{32}^{(1)}\ast x_2+b_3^{(1)}\end{array}$$

（2）非线性层

$$\{\begin{array}{c}{a}_1^{(1)}=f(z_1^{(1)})\\ a_2^{(1)}=f(z_2^{(1)})\\ a_3^{(1)}=f(z_3^{(1)})\end{array}$$

（3）矩阵化

$$X^{(1)}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$
$$Z^{(1)}=\left[\begin{array}{c}{z}_1^{(1)}\\ z_2^{(1)}\\ z_3^{(1)}\end{array}\right]$$

$$W^{(1)}=\left[\begin{array}{cc}{w}_{11}^{(1)}& w_{12}^{(1)}\\ w_{21}^{(1)}& w_{22}^{(1)}\end{array}\right]$$
$$B^{(1)}=\left[\begin{array}{c}{b}_1^{(1)}\\ b_2^{(1)}\\ b_3^{(1)}\end{array}\right]$$
$$Z^{(1)}=W^{(1)}\ast X^{(1)}+B^{(1)}$$

2、第二层

$$\{\begin{array}{c}{z}_1^{(2)}=w_{11}^{(2)}\ast a_1^{(1)}+w_{12}^{(2)}\ast a_2^{(1)}+w_{13}^{(2)}\ast a_3^{(1)}+b_1^{(2)}\\ z_2^{(2)}=w_{21}^{(2)}\ast a_1^{(1)}+w_{22}^{(2)}\ast a_2^{(1)}+w_{23}^{(2)}\ast a_3^{(1)}+b_2^{(2)}\\ z_3^{(2)}=w_{31}^{(2)}\ast a_1^{(1)}+w_{32}^{(2)}\ast a_2^{(1)}+w_{33}^{(2)}\ast a_3^{(1)}+b_3^{(2)}\end{array}$$

非线性层

$$\{\begin{array}{c}{a}_1^{(2)}=f(z_1^{(2)})\\ a_2^{(2)}=f(z_2^{(2)})\\ a_3^{(2)}=f(z_3^{(2)})\end{array}$$

3、第三层

$$\{\begin{array}{c}{z}_1^{(3)}=w_{11}^{(3)}\ast a_1^{(2)}+w_{12}^{(3)}\ast a_2^{(2)}+w_{13}^{(3)}\ast a_3^{(2)}+b_1^{(3)}\\ z_2^{(3)}=w_{21}^{(3)}\ast a_1^{(2)}+w_{22}^{(3)}\ast a_2^{(2)}+w_{23}^{(3)}\ast a_3^{(2)}+b_2^{(3)}\end{array}$$

非线性层

$$\{\begin{array}{c}{a}_1^{(3)}=f(z_1^{(3)})\\ a_2^{(3)}=f(z_2^{(3)})\end{array}$$

4、输出层

$$\{\begin{array}{c}{y}_1=a_1^{(3)}\\ y_2=a_2^{(3)}\end{array}$$

5、计算损失函数

$$loss=\frac{1}{2}|y_{ref}-y_{des}{|}^2$$
展开损失：
$$loss=\frac{1}{2}[(y_1-y_{1_{des}}{)}^2+(y_2-y_{2_{des}}{)}^2]$$

二、后向传播

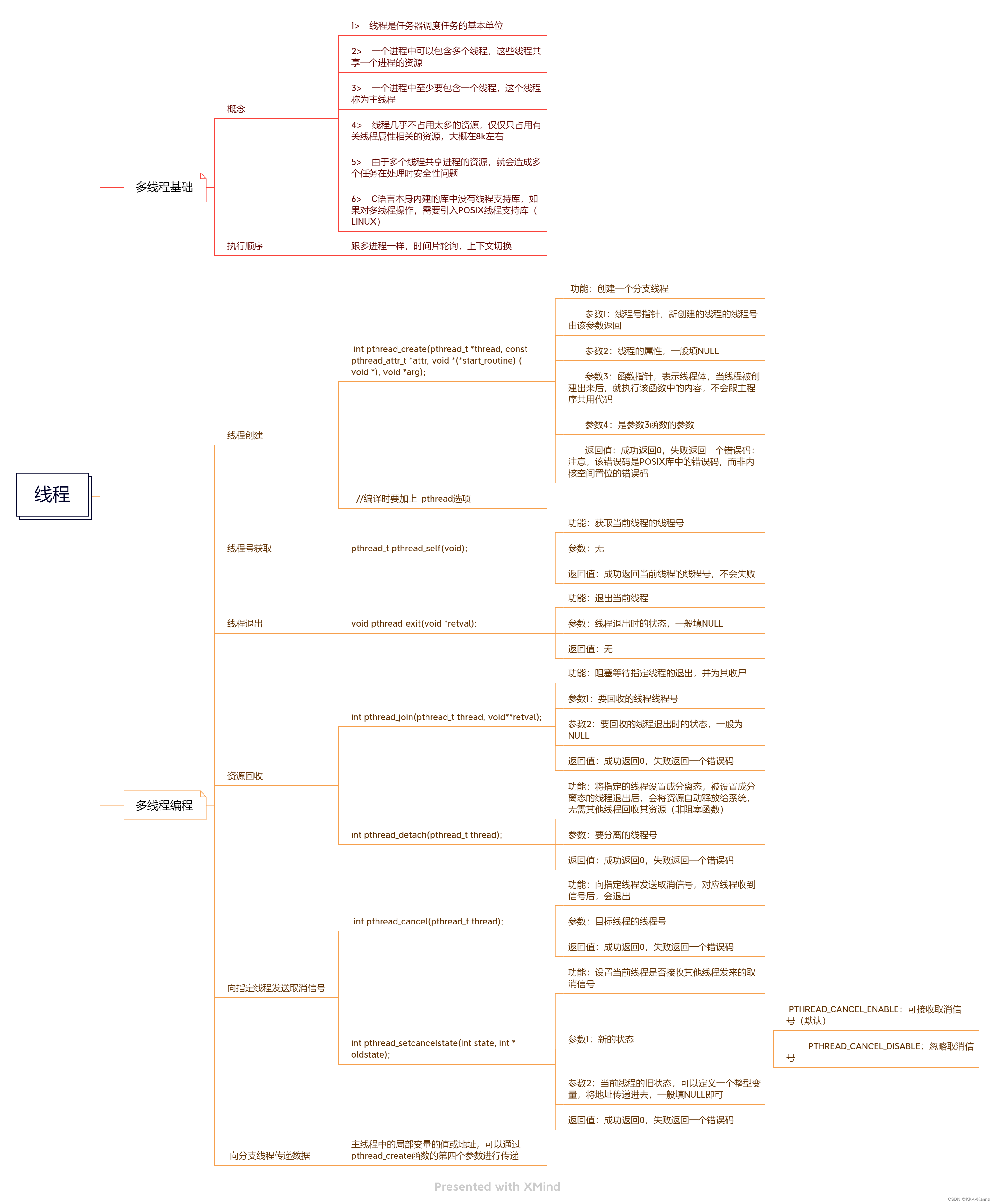
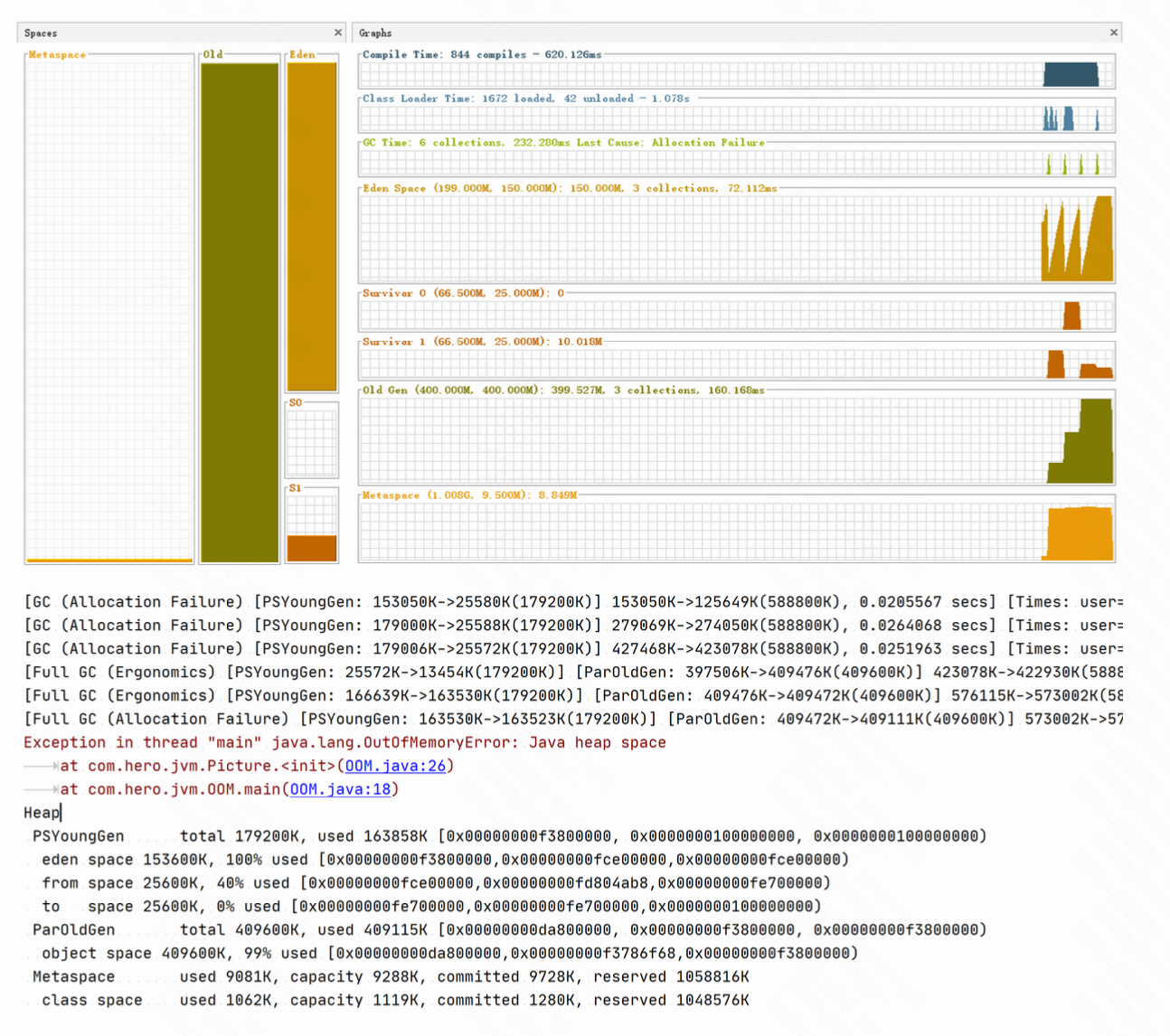
1、更新参数

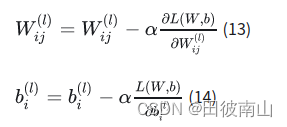
2、定义误差项

3、通过误差项计算两个偏导

（1）计算最后一层δ

单个误差项

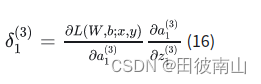
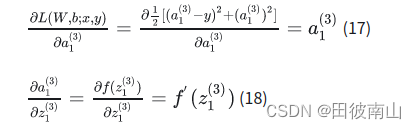
结合上面三个公式：

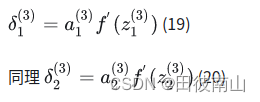
（2）推导前一层的δ

利用前向传播的链式法则：

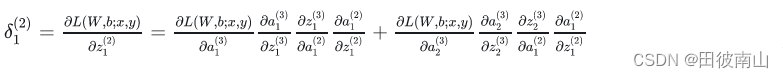
每项的前三个就是后一层的误差项：

计算上面公式中的三个偏导，得出下式：

考虑同一层的误差项目，写成一般形式：

（3）计算偏导

关于权重的偏导

关于偏置的偏导