【力扣hot100】刷题笔记Day7

news2024/10/5 20:24:31

前言

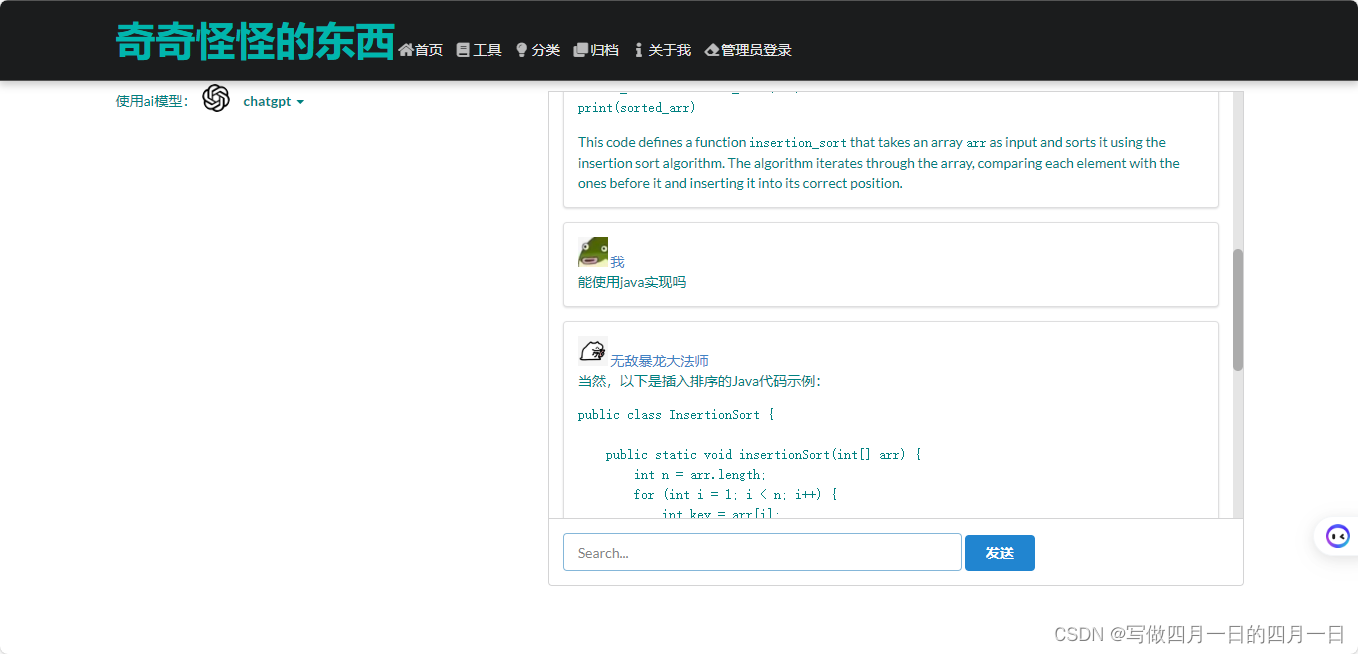
身边同学已经陆陆续续回来啦，舍友都开始投简历了，我也要加油啦！刷完hot100就投！

73. 矩阵置零 - 力扣（LeetCode）

标记数组：空间复杂度O(m+n)

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m, n = len(matrix), len(matrix[0])
        row, col = [False] * m, [False] * n  # 标记数组
        # 遍历一次，标记对应的行列为0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    row[i] = col[j] = True
        # 遍历二次，根据标记修改对应行列
        for i in range(m):
            for j in range(n):
                if row[i] or col[j]:
                    matrix[i][j] = 0

两个标记变量：空间复杂度O(1)

思路参考题解，遇到0就向首行首列汇报，最后再把首行首列置0

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m, n = len(matrix), len(matrix[0])
        # 如果可迭代对象中有任何一个元素为 True，则 any 函数返回 True；否则返回 False
        flag_col0 = any(matrix[i][0] == 0 for i in range(m))  # 判断首行是否有0
        flag_row0 = any(matrix[0][j] == 0 for j in range(n))  # 判读首列是否有0
        # 迭代非首行非首列，遇到0就把置0指令放在首行首列
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = matrix[0][j] = 0
        # 迭代非首行非首列，根据指令置0
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0
        # 首行有0，则全置0
        if flag_col0:
            for i in range(m):
                matrix[i][0] = 0
        # 首列有0，则全置0
        if flag_row0:
            for j in range(n):
                matrix[0][j] = 0

一个标记变量：空间复杂度O(1)

参考题解，保存首行，但是要全部倒序遍历，防止提前更新，太难想仅作参考

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m = len(matrix)
        n = len(matrix[0])
        first_row = False   # 标记首行是否有0元素
        for i, row in enumerate(matrix):
            for j, item in enumerate(row):
                if i == 0 and item == 0:
                    first_row = True    # 首行出现0元素，用标志位标记
                elif item == 0:
                    matrix[i][0] = 0    # 非首行出现0元素，将对应的列首置为0，说明该列要置为0
                    matrix[0][j] = 0    # 将对应的行首置为0，说明该行要置为0
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                # 从最后一个元素反向遍历，避免行首和列首的信息被篡改
                if i == 0 and first_row:
                    matrix[i][j] = 0    # 首行元素是否置为0看标志位
                elif i != 0 and (matrix[i][0] == 0 or matrix[0][j] == 0):
                    matrix[i][j] = 0    # 非首行元素是否置为0看行首和列首是否为0

54. 螺旋矩阵 - 力扣（LeetCode）

边界模拟

类似之前C++版本，设置边界，依次循环模拟输出，边界溢出则跳出循环

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        l, r, u, d = 0, len(matrix[0])-1, 0, len(matrix)-1
        while True:
            # 向右
            for i in range(l, r+1): res.append(matrix[u][i])
            u += 1
            if u > d: break
            # 向下
            for i in range(u, d+1): res.append(matrix[i][r])
            r -= 1
            if r < l: break
            # 向左
            for i in range(r, l-1, -1): res.append(matrix[d][i])
            d -= 1
            if d < u: break
            # 向上
            for i in range(d, u-1, -1): res.append(matrix[i][l])
            l += 1
            if l > r: break
        return res

48. 旋转图像 - 力扣（LeetCode）

辅助数组

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        matrix_new = [[0] * n for _ in range(n)]  # 新的n*n的矩阵
        for i in range(n):
            for j in range(n):
                # matrix[row][col]旋转到matrix_new[col][n−row−1]
                matrix_new[j][n-i-1] = matrix[i][j]
        # 不能写成 matrix = matrix_new
        matrix[:] = matrix_new

原地旋转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n // 2):  # 偶数n/2，奇数(n-1)/2
            for j in range((n + 1) // 2):  # 偶数n/2，奇数(n+1)/2
                matrix[i][j], matrix[n-j-1][i], matrix[n-i-1][n-j-1], matrix[j][n-i-1] \
                = matrix[n-j-1][i], matrix[n-i-1][n-j-1], matrix[j][n-i-1], matrix[i][j]

两次翻转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # 上下翻转：只遍历上半部
        for i in range(n // 2):
            for j in range(n):
                matrix[i][j], matrix[n-i-1][j] = matrix[n-i-1][j], matrix[i][j]
        # 对角翻转：只遍历下三角
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

240. 搜索二维矩阵 II - 力扣（LeetCode）

直接搜索：N(mn)

就不用传统的遍历写法了，这里记录两种仅用一行就可以实现的搜索算法

class Solution:
    def searchMatrix(self, M: List[List[int]], target: int) -> bool:
    # chain()函数于将多个可迭代对象连接成一个单独的迭代器
    # 这里用于连接多个被*M解包得到的多个一维列表   
    return target in chain(*M)
    # 直接利用sum函数转化为一个一维列表
    return target in sum(M,[])

二分查找：N(log(mn))

class Solution:
    def searchMatrix(self, M: List[List[int]], target: int) -> bool:
        def bin_search(arr,target):
            l,r = 0,len(arr)-1
            while l <= r:
                mid = (l+r) // 2
                if arr[mid] == target:
                    return True
                elif arr[mid] < target:
                    l = mid + 1
                else:
                    r = mid - 1
            return False
        m = len(M)
        # 逐行进行二分查找
        for i in range(m):
            if bin_search(M[i], target):
                return True
        return False

贪心BST

也叫折线搜索，来源于题解，图画的很清晰，从右上角出发进行搜索

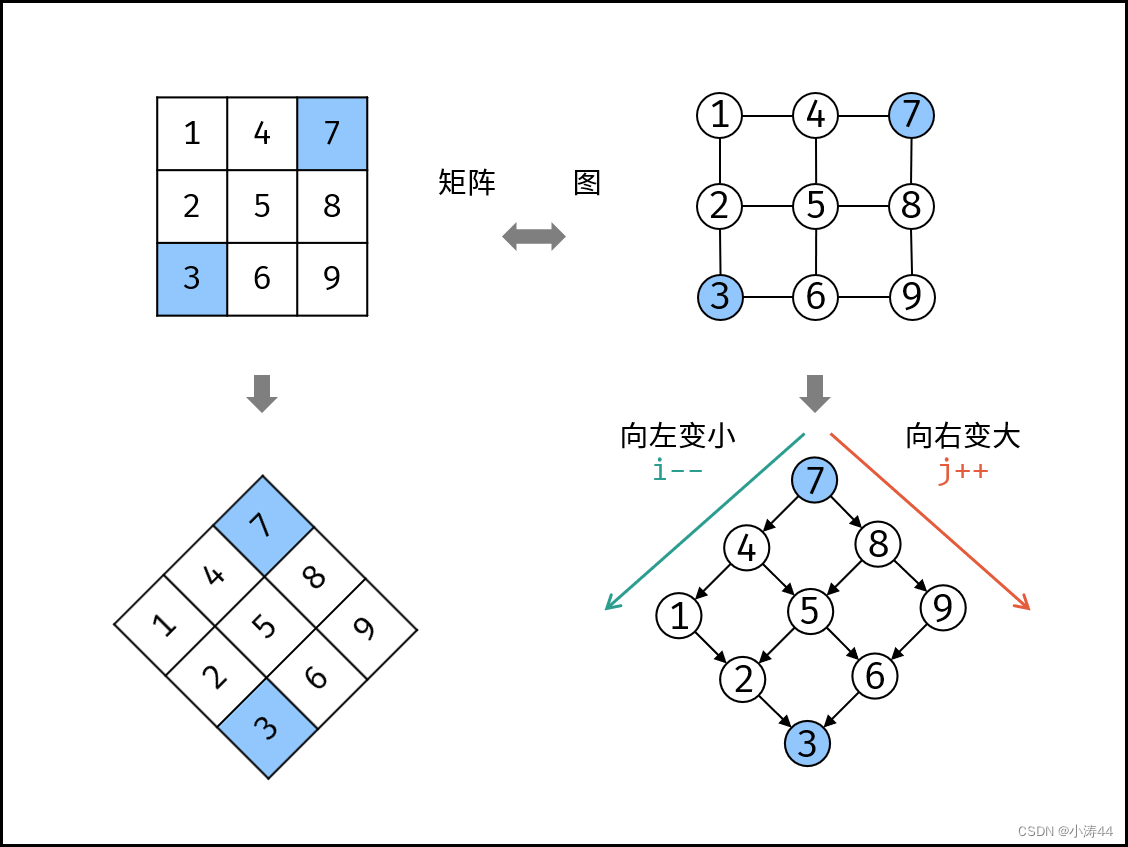
class Solution:
    def searchMatrix(self, M: List[List[int]], target: int) -> bool:
        i, j = len(M) - 1, 0
        # 右上角出发进行搜索
        while i >= 0 and j <= len(M[0]) - 1:
            if target > M[i][j]:
                j += 1  # 往下移，排除一行
            elif target < M[i][j]:
                i -= 1  # 往左移，排除一列
            else:
                return True
        return False