【二十五】【C++】二叉搜索树及其简单实现

二叉搜索树的性质

二叉搜索树（BST）是一种特殊的二叉树，它具有以下性质：

每个节点都有一个键（或值），并且每个节点最多有两个子节点。
左子树上所有节点的键都小于其根节点的键。
右子树上所有节点的键都大于其根节点的键。
左右子树也都是二叉搜索树。

二叉搜索树的常见方法

1. 插入节点（Insertion）

插入操作是将一个新的键值对添加到二叉搜索树中。插入过程需要保证树的二叉搜索属性：节点的左子树只包含小于节点键的节点，节点的右子树只包含大于节点键的节点。

2. 搜索节点（Search）

搜索操作用于在二叉搜索树中查找一个键。如果键存在，返回对应的节点；否则，返回nullptr或一些标志值表示键不存在。

3. 删除节点（Deletion）

删除操作涉及三种情况：

叶子节点：直接删除。
一个子节点：删除节点并用其子节点替代。
两个子节点：用其右子树的最小节点（或左子树的最大节点）替代该节点，然后删除那个最小（或最大）节点。

4. 遍历（Traversal）

二叉树的遍历通常有三种方式：前序（Pre-order）、中序（In-order）和后序（Post-order）遍历。对于二叉搜索树，中序遍历会按照键的升序访问所有节点。

二叉搜索树的中序遍历

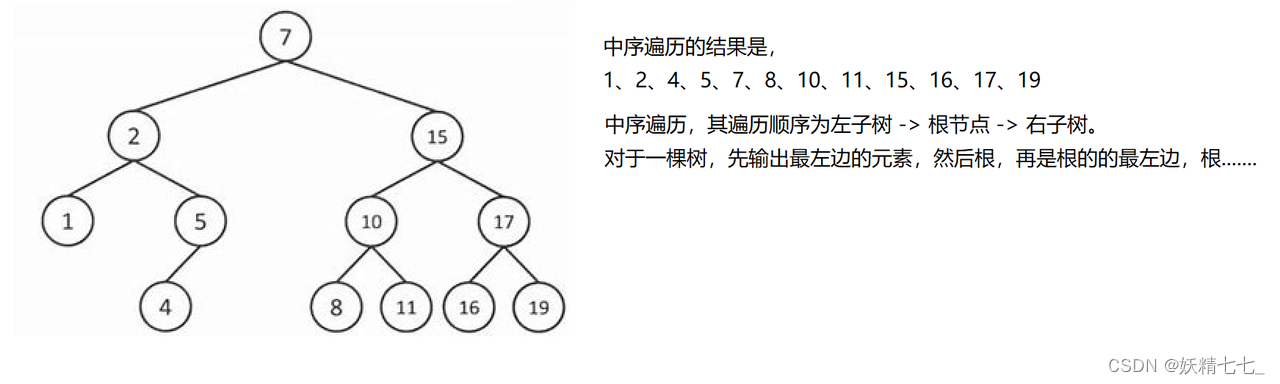
二叉搜索树（Binary Search Tree，BST）的中序遍历是指按照从小到大的顺序访问树中的所有节点。这种遍历方式是一种有序遍历，因为BST的性质保证了中序遍历的结果是有序的。

中序遍历，其遍历顺序为左子树 -> 根节点 -> 右子树。对于每一个小的单元，其左子树的值比根节点的值小，右子树的值比根节点的值大。中序遍历过程中，对于每一个单元都保证了值的从小到大输出。而对于单元的输出顺序，又满足最左边即最小的单元，依次变大。所以二叉搜索树的中序遍历，输出的结果就是值的升序序列。

二叉搜索又称作排序二叉树。因为其中序遍历输出的结果的有序的。

5. 查找最小和最大键（Finding Minimum and Maximum Key）

在二叉搜索树中查找最小和最大键很简单：沿左子树一直向下遍历可以找到最小键，而沿右子树一直向下遍历可以找到最大键。

6. 高度和深度（Height and Depth）

树的高度是从根节点到最远叶子节点的最长路径上的边数。树的深度是从根节点到某节点的路径上的边数。计算树的高度通常通过递归实现。

二叉搜索树的简单实现


#include <iostream>
using namespace std;


template<class T>
struct BSTNode {
    BSTNode(const T& x = T())
        : left(nullptr)
        , right(nullptr)
        , data(x)
    {}

    BSTNode<T>* left;
    BSTNode<T>* right;
    T data;
 };


// 假设：树中节点的值域唯一
template<class T>
class BinarySearchTree {
        typedef BSTNode<T> Node;

    public:
        BinarySearchTree()
            : root(nullptr)
        {}

        ~BinarySearchTree() {
            Destroy(root);
        }

        bool Insert(const T& data) {
            // 1. 空树---
            // 新插入的节点应该是跟节点
            if (nullptr == root) {
                root = new Node(data);
                return true;
            }

            // 2. 树非空
            // a. 找待插入节点在树中的位置--->按照二叉搜索树的性质
            Node* cur = root;
            Node* parent = nullptr;
            while (cur) {
                parent = cur;
                if (data < cur->data)
                    cur = cur->left;
                else if (data > cur->data)
                    cur = cur->right;
                else
                    return false;
            }

            // 树中不存在值为data的节点
            // b. 插入新节点
            cur = new Node(data);
            if (data < parent->data)
                parent->left = cur;
            else
                parent->right = cur;

            return true;
        }

        Node* Find(const T& data)const {
            Node* cur = root;
            while (cur) {
                if (data == cur->data)
                    return cur;
                else if (data < cur->data)
                    cur = cur->left;
                else
                    cur = cur->right;
            }

            return nullptr;
        }

        bool Erase(const T& data) {
            // 1. 先找data是否存在
            Node* cur = root;
            Node* parent = nullptr;
            while (cur) {
                if (data == cur->data)
                    break;
                else if (data < cur->data) {
                    parent = cur;
                    cur = cur->left;
                } else {
                    parent = cur;
                    cur = cur->right;
                }
            }

            // 值为data的节点不存在
            if (nullptr == cur)
                return false;

            // 2. 找到值为data的节点，即cur--->将该节点删除掉
            // 删除节点并且保存树的关系

            // 有些节点可以直接删除，但是有些节点不能直接删除
            // 需要对cur子树分情况讨论
            // 1. cur是叶子
            // 2. cur只有左孩子
            // 3. cur只有右孩子
            // 4. cur左右孩子均存在
            // 经过图解分析发现：
            // 情况1实际可以和情况2或者情况3合并起来
            Node* pDelNode = cur;
            if (nullptr == cur->left) {
                // 说明cur可能是叶子节点，也可能是只有右孩子
                if (nullptr == parent) {
                    // 删除cur刚好是根节点，且根没有左子树
                    root = cur->right;
                } else {
                    // cur的双亲存在
                    if (cur == parent->left)
                        parent->left = cur->right;
                    else
                        parent->right = cur->right;
                }
            } else if (nullptr == cur->right) {
                // 说明cur只有左孩子
                if (nullptr == parent) {
                    // cur是根节点且根没有右子树，注意：左子树是一定存在的
                    root = cur->left;
                } else {
                    if (cur == parent->left)
                        parent->left = cur->left;
                    else
                        parent->right = cur->left;
                }
            } else {
                // 说明cur左孩孩子均存在
                // 1. 在cur的子树中找替代节点，并保存其双亲
                // 左子树：找最大的即最右侧节点
                // 右子树：找最小的即最左侧节点---即中序遍历的第一个节点--和数据结构书本保持一致
                pDelNode = cur->right;
                parent = cur;
                while (pDelNode->left) {
                    parent = pDelNode;
                    pDelNode = pDelNode->left;
                }

                // 2. 将替代节点中的值交给cur
                cur->data = pDelNode->data;

                // 3. 删除替代节点
                if (pDelNode == parent->left)
                    parent->left = pDelNode->right;
                else
                    parent->right = pDelNode->right;
            }

            delete pDelNode;
            return true;
        }

        void InOrder() {
            _InOrder(root);
            cout << endl;
        }

    private:
        void _InOrder(Node* proot) {
            if (proot) {
                _InOrder(proot->left);
                cout << proot->data << " ";
                _InOrder(proot->right);
            }
        }

        void Destroy(Node*& proot) {
            if (proot) {
                Destroy(proot->left);
                Destroy(proot->right);
                delete proot;
                proot = nullptr;
            }
        }


    private:
        BSTNode<T>* root;
 };


void TestBSTree() {
    BinarySearchTree<int> t;
    int a[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
    for (auto e : a)
        t.Insert(e);

    t.InOrder();

    BSTNode<int>* cur = t.Find(9);
    if (cur) {
        cout << "9 is in BSTree" << endl;
    } else {
        cout << "9 is not in BSTree" << endl;
    }

    cur = t.Find(13);
    if (cur) {
        cout << "13 is in BSTree" << endl;
    } else {
        cout << "13 is not in BSTree" << endl;
    }

    t.Erase(7);
    t.InOrder();

    t.Erase(0);
    t.InOrder();

    t.Erase(5);
    t.InOrder();
 }

int main() {
    TestBSTree();
 }

代码解析

BSTNode 结构体定义

template<class T>
struct BSTNode {
    BSTNode(const T& x = T())
        : left(nullptr)
        , right(nullptr)
        , data(x)
    {}

    BSTNode<T>* left;
    BSTNode<T>* right;
    T data;
 };

这段代码定义了一个模板结构体 BSTNode，用于表示二叉搜索树（BST）的节点。

template<class T>：这是一个模板声明，声明了一个模板类型 T，它表示节点中存储的数据类型。

BSTNode(const T& x = T())：这是结构体的构造函数，用于初始化节点对象。它接受一个参数 x，默认值为类型 T 的默认构造值。这样设计使得创建节点对象时，可以不传入参数，默认构造出一个具有默认值的节点。

left(nullptr) 和 right(nullptr)：这两行初始化了节点的左右子节点指针，初始值为 nullptr，表示这个节点暂时没有左右子节点。

data(x)：这一行初始化了节点中存储的数据 data，其值为构造函数传入的参数 x。

BSTNode<T>* left; 和 BSTNode<T>* right;：这两行定义了指向左右子节点的指针，它们的类型为 BSTNode<T>*，即指向 BSTNode 类型的指针。这样的设计使得可以构建二叉树的数据结构，通过这些指针连接各个节点。

T data;：这一行定义了节点中存储的数据成员 data，其类型为模板参数 T，表示节点存储的数据类型。

BinarySearchTree 类定义

template<class T>
class BinarySearchTree {
    typedef BSTNode<T> Node;
public:
    BinarySearchTree() : root(nullptr) {}
    ~BinarySearchTree() {
        Destroy(root);
    }
    // 其他成员函数...
private:
    BSTNode<T>* root;

};

这段代码定义了一个模板类 BinarySearchTree，用于表示二叉搜索树（BST）。

template<class T>：这是一个模板声明，声明了一个模板类型 T，它表示树中存储的数据类型。

typedef BSTNode<T> Node;：这行代码定义了一个别名 Node，它表示 BSTNode<T> 类型，即树节点的类型。

BinarySearchTree() : root(nullptr) {}：这是类的默认构造函数。在其中，根节点 root 被初始化为 nullptr，表示空树。

~BinarySearchTree() { Destroy(root); }：这是类的析构函数。它调用了私有成员函数Destroy(root)，用于销毁整棵树。通过递归的方式，首先销毁根节点的子树，然后销毁根节点本身。这样可以确保释放树中所有节点占用的内存，避免内存泄漏。

BSTNode<T>* root;：这一行定义了一个指针成员 root，用于指向树的根节点。这个指针的类型为BSTNode<T>*，即指向 BSTNode 类型的指针，其中 T 是模板参数，表示节点存储的数据类型。

插入操作 (Insert 函数)

        bool Insert(const T& data) {
            // 1. 空树---
            // 新插入的节点应该是跟节点
            if (nullptr == root) {
                root = new Node(data);
                return true;
            }

            // 2. 树非空
            // a. 找待插入节点在树中的位置--->按照二叉搜索树的性质
            Node* cur = root;
            Node* parent = nullptr;
            while (cur) {
                parent = cur;
                if (data < cur->data)
                    cur = cur->left;
                else if (data > cur->data)
                    cur = cur->right;
                else
                    return false;
            }

            // 树中不存在值为data的节点
            // b. 插入新节点
            cur = new Node(data);
            if (data < parent->data)
                parent->left = cur;
            else
                parent->right = cur;

            return true;
        }

这是一个公有成员函数 Insert，用于向二叉搜索树中插入新节点。它接收一个参数 data，表示要插入的节点的数据。

首先检查树是否为空。如果树为空（即根节点 root 为 nullptr），则将新节点直接作为根节点插入，并返回 true。

如果树非空，则需要找到新节点在树中的插入位置。根据二叉搜索树的性质，如果新节点的值小于当前节点的值，则应该往左子树方向查找插入位置；如果新节点的值大于当前节点的值，则应该往右子树方向查找插入位置。通过循环遍历直到找到合适的插入位置。

找到插入位置后，根据新节点的值与其父节点的值的比较结果，确定将新节点插入到父节点的左子树还是右子树。然后创建新节点，并将其连接到父节点相应的子树中。最后返回 true，表示插入操作成功。

查找操作 (Find 函数)

        Node* Find(const T& data)const {
            Node* cur = root;
            while (cur) {
                if (data == cur->data)
                    return cur;
                else if (data < cur->data)
                    cur = cur->left;
                else
                    cur = cur->right;
            }

            return nullptr;
        }

这是一个公有成员函数 Find，用于在二叉搜索树中查找具有特定值的节点。它接收一个参数 data，表示要查找的节点的值，并返回指向该节点的指针。

首先将当前节点指针 cur 初始化为根节点 root。然后开始一个循环，该循环会在树中查找目标节点，直到遇到空节点为止。

在循环中，首先检查当前节点的值是否等于目标值 data。如果相等，则找到了目标节点，直接返回当前节点指针。如果目标值小于当前节点的值，则应该继续在左子树中查找；反之，则在右子树中查找。根据比较结果更新当前节点指针 cur，继续向下搜索。

如果循环结束时仍未找到目标节点，则说明树中不存在值为 data 的节点，此时返回 nullptr，表示未找到目标节点。

删除操作 (Erase 函数)

        bool Erase(const T& data) {
            // 1. 先找data是否存在
            Node* cur = root;
            Node* parent = nullptr;
            while (cur) {
                if (data == cur->data)
                    break;
                else if (data < cur->data) {
                    parent = cur;
                    cur = cur->left;
                } else {
                    parent = cur;
                    cur = cur->right;
                }
            }

            // 值为data的节点不存在
            if (nullptr == cur)
                return false;

            // 2. 找到值为data的节点，即cur--->将该节点删除掉
            // 删除节点并且保存树的关系

            // 有些节点可以直接删除，但是有些节点不能直接删除
            // 需要对cur子树分情况讨论
            // 1. cur是叶子
            // 2. cur只有左孩子
            // 3. cur只有右孩子
            // 4. cur左右孩子均存在
            // 经过图解分析发现：
            // 情况1实际可以和情况2或者情况3合并起来
            Node* pDelNode = cur;
            if (nullptr == cur->left) {
                // 说明cur可能是叶子节点，也可能是只有右孩子
                if (nullptr == parent) {
                    // 删除cur刚好是根节点，且根没有左子树
                    root = cur->right;
                } else {
                    // cur的双亲存在
                    if (cur == parent->left)
                        parent->left = cur->right;
                    else
                        parent->right = cur->right;
                }
            } else if (nullptr == cur->right) {
                // 说明cur只有左孩子
                if (nullptr == parent) {
                    // cur是根节点且根没有右子树，注意：左子树是一定存在的
                    root = cur->left;
                } else {
                    if (cur == parent->left)
                        parent->left = cur->left;
                    else
                        parent->right = cur->left;
                }
            } else {
                // 说明cur左孩孩子均存在
                // 1. 在cur的子树中找替代节点，并保存其双亲
                // 左子树：找最大的即最右侧节点
                // 右子树：找最小的即最左侧节点---即中序遍历的第一个节点--和数据结构书本保持一致
                pDelNode = cur->right;
                parent = cur;
                while (pDelNode->left) {
                    parent = pDelNode;
                    pDelNode = pDelNode->left;
                }

                // 2. 将替代节点中的值交给cur
                cur->data = pDelNode->data;

                // 3. 删除替代节点
                if (pDelNode == parent->left)
                    parent->left = pDelNode->right;
                else
                    parent->right = pDelNode->right;
            }

            delete pDelNode;
            return true;
        }

这是一个公有成员函数 Erase，用于删除二叉搜索树中值为 data 的节点。它接收一个参数 data，表示要删除的节点的值，并返回一个布尔值，表示删除操作是否成功。

首先在树中找到值为 data 的节点。通过循环遍历，如果当前节点的值等于目标值 data，则找到了目标节点；如果目标值小于当前节点的值，则继续在左子树中查找；反之，则在右子树中查找。如果循环结束时，当前节点为空，则说明树中不存在值为 data 的节点，直接返回 false 表示删除失败。

在找到目标节点后，根据不同情况进行删除操作：

如果目标节点是叶子节点或者只有一个子节点，直接删除该节点并将其子节点连接到其父节点上。

如果目标节点有两个子节点，则需要找到它的后继节点（右子树中的最小节点）或者前驱节点（左子树中的最大节点）来替代它，保持二叉搜索树的有序性。将后继/前驱节点的值复制到目标节点上，然后再删除后继/前驱节点。

最后，释放被删除节点的内存并返回 true 表示删除成功。

中序遍历 (InOrder 和 _InOrder 函数)

        void InOrder() {
            _InOrder(root);
            cout << endl;
        }

    private:
        void _InOrder(Node* proot) {
            if (proot) {
                _InOrder(proot->left);
                cout << proot->data << " ";
                _InOrder(proot->right);
            }
        }

这段代码实现了二叉搜索树的中序遍历，并提供了一个公有成员函数 InOrder() 用于调用中序遍历，并提供了一个私有辅助函数 _InOrder(Node* proot) 用于实际执行递归的中序遍历操作。

InOrder() 是一个公有成员函数，用于对二叉搜索树进行中序遍历。它调用了私有成员函数_InOrder(Node* proot) 来执行中序遍历操作，传入根节点 root 作为参数，并在遍历结束后输出换行符，以便在打印完所有节点后换行。

_InOrder(Node* proot) 是一个私有成员函数，用于实际执行递归的中序遍历操作。它接收一个参数proot，表示当前子树的根节点。在函数体内，先判断当前节点是否为空，如果不为空，则递归地对左子树进行中序遍历 _InOrder(proot->left)，然后输出当前节点的值 cout << proot->data << " ";，最后递归地对右子树进行中序遍历 _InOrder(proot->right)。

这样，通过调用 InOrder() 函数，可以完成对整棵二叉搜索树的中序遍历，并按照升序打印出各个节点的值。

销毁树 (Destroy 函数)

        void Destroy(Node*& proot) {
            if (proot) {
                Destroy(proot->left);
                Destroy(proot->right);
                delete proot;
                proot = nullptr;
            }
        }

这段代码实现了一个递归函数 Destroy，用于销毁二叉搜索树。

这是一个公有成员函数 Destroy，用于销毁二叉搜索树。它接收一个参数 proot，表示当前子树的根节点的引用。这里使用引用是因为在函数中会修改根节点的指针，将其置为 nullptr。

首先检查当前节点是否为空，如果为空，则表示当前子树已经被销毁或者是空树，直接返回。如果不为空，则执行销毁操作。

递归调用 Destroy 函数，分别对当前节点的左子树和右子树进行销毁操作。通过递归，可以先销毁左子树，再销毁右子树，最后再销毁当前节点，从而实现对整棵树的销毁。

在递归回溯的过程中，当左右子树都被销毁之后，对当前节点进行销毁操作。首先释放当前节点占用的内存，然后将当前节点指针置为 nullptr，以避免出现悬空指针。这里使用了引用 Node*& proot，使得在函数外部调用 Destroy 函数后，根节点的指针也会被置为 nullptr，从而确保树被正确销毁。

这样，通过调用 Destroy 函数，可以销毁整棵二叉搜索树，释放所有节点占用的内存。