目录
1 AR 1
2 MA 1
3 ARMA 1
4 ARMAX 2
5 ARX 2
6 ARARX 3
7 ARARMAX 3
8 OE 3
9 BJ 3
各种线性模型,这些模型算数学基础模型,不仅在计量经济学,也在工业控制等各领域有应用。包括AR、MA、ARMA、ARMAX、ARX、ARARMAX、OE、BJ等。
1 AR
自回归模型(Autoregressive model,简称AR模型)。指x与x自己之前的状态(t-i)相关,公式如下:
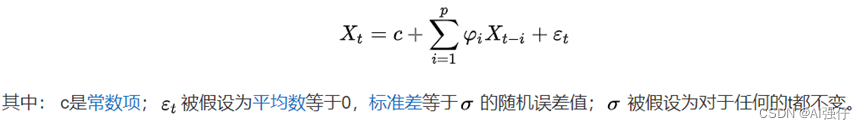
2 MA
q阶移动平均(moving average)模型,简记为MA(q)。主要指x和随机误差(噪声)ε及之前t-i的随机误差(噪声)ε有关,公式如下:
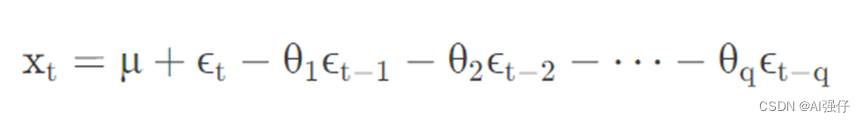
3 ARMA
自回归滑动平均模型(Autoregressive moving average model,简称:ARMA模型)。是研究时间序列的重要方法,如模型标题所述,ARMA由自回归模型(简称AR模型)与移动平均模型(简称MA模型)为基础“混合”构成。
公式如下,将x换成了y,一个意思。即y和(t-q)之前的y、(t-q)的随机误差ε、t时的ε相关。
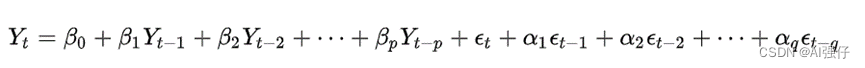
4 ARMAX
ARMAX(Autoregressive Moving Average with Extra Input)。
在ARMA基础上增加了一个额外输入项u,公式如下,其中e指ε:
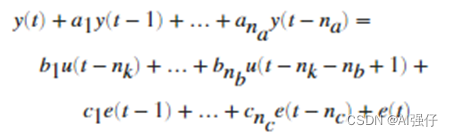
矩阵表示可简化为,其中q表示向前追溯:
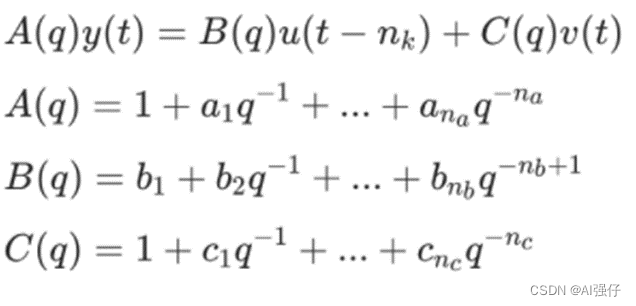

即A(q)提供了输入和噪声共同的极点(分母为0时,A(q)移到等式右边就变为分母了),B(q)时提供输入零点。
5 ARX
有源自回归(Auto-Regressive with Extra Inputs,ARX)模型。ARX就是AR模型加了一个额外输入。或者说ARX等于ARMAX去掉MA,即去掉(t-q)之前的随机误差ε,也就是去掉ARMAX公式的C,如下,v(t)只是当前随机误差,无(t-q)之前的:
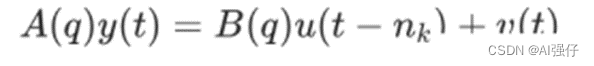
6 ARARX
可以看到和ARMAX很像,C变成1/D,分子变分母,就增加了极点(分母等于0时),提供了噪声(误差)的极点表示。其中A(q)提供了输入和噪声共同的极点,而D只是提供噪声的极点。
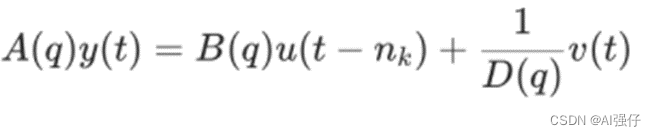
7 ARARMAX
在ARMAX基础上增加了1/D,即不仅有C也有D。
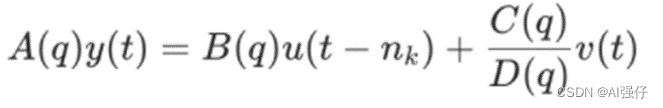
8 OE
输出误差模型(output error)。
不同于ARX的是,没有了A(q),即没有提供了输入和噪声共同的极点;而是换成了F,只提供输入的极点。

9 BJ
Box-Jenkins模型。在OE模型基础上增加了C、D,故BJ模型对输入和噪声均可独立建模。
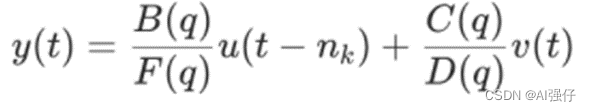



![P1308 [NOIP2011 普及组] 统计单词数————C++](https://img-blog.csdnimg.cn/5232a83cf1ff4062af86acb710379379.png)