算法学习系列（三十六）：树状数组与线段树

引言

在算法竞赛当中，这个树状数组和线段树用的还是比较多的，树状数组是用来动态的求前缀和的，而线段树的功能是包含树状数组的，相当于一个大砍刀，什么都能做，而且出题点也是比较多的，所以得好好对待好好学啊。

一、树状数组

1.概念

功能：能够动态的求前缀和
时间复杂度 $l o g N$ ，修改和查询都是
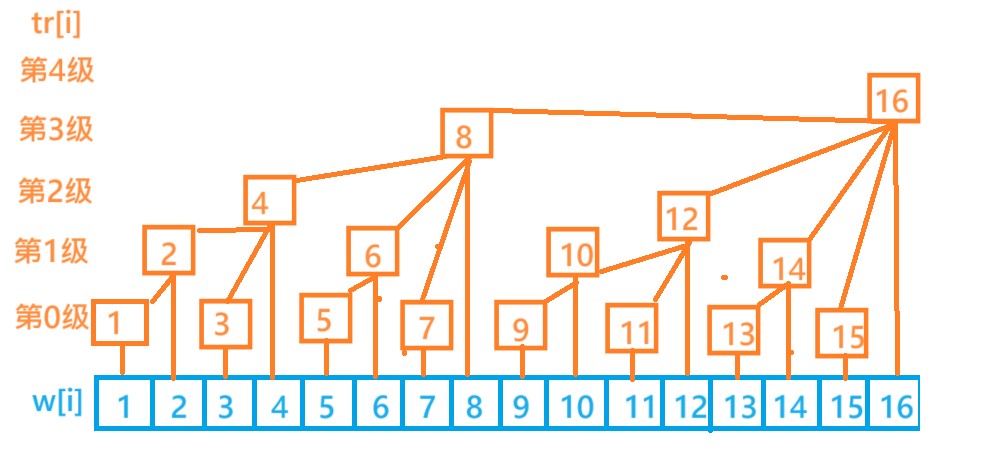
思路： $t r [i]$ 存的是 $(x - l o w bi t (x), x]$ 的和，相当于只存了一段的前缀和，然后查询和修改只把一段又一段的前缀和一修改就行了，只用修改 $l o g N 个$ ，而不用修改 $N 个$
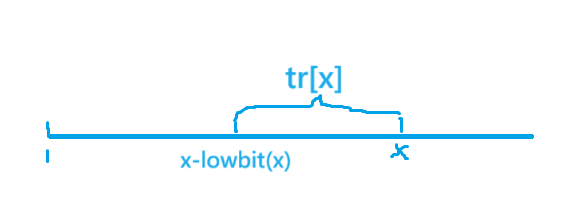
在这里插入图片描述

lowbit(x):x的二进制数末尾有几个零
树状数组大概就长如下图的样子：
在这里插入图片描述

2.代码模板

const int N = 1e5+10;

int n, m;
int w[N], tr[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)  //修改的话减去原来的加上现在的即可
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int query(int x)  //求x的前缀和
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

3.例题

动态求连续区间和

思路：模板题

题目描述：

给定  n  个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。
第二行包含 n个整数，表示完整数列。
接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。
数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000,1≤m≤100000，1≤a≤b≤n,
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例：
11
30
35

示例代码：

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5+10;

int n, m;
int w[N], tr[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int query(int x)  //查询x的前缀和
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    for(int i = 1; i <= n; ++i) add(i,w[i]);
    
    while(m--)
    {
        int k, a, b;
        scanf("%d%d%d", &k, &a, &b);
        if(k) add(a,b);
        else printf("%d\n", query(b) - query(a-1));  //前缀和思想
    }
    
    return 0;
}

数星星

思路：这个其实问左下方的星星有多少个就是几级的，由于输入是按从下往上从左往右的顺序输入，所以到该星星的时候，不会有比它还上的了，所以只需要判断之前谁的x比它小于等于就行了，可以抽象为一个数组，每个数组的下标i表示当前横坐标为i的星星有几个，要求的等级就是该下标的前缀和，又因为相当是动态插入的星星所以用树状数组比较好。

题目描述：

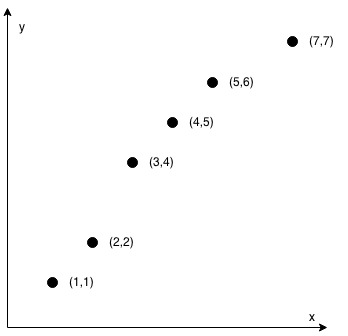
天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式
第一行一个整数 N，表示星星的数目；
接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；
不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式
N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围
1≤N≤15000,0≤x,y≤32000
输入样例：
5
1 1
5 1
7 1
3 3
5 5
输出样例：
1
2
1
1
0

示例代码：

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 32010;

int n;
int tr[N], res[N];  //res[i]代表第i级的数量

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)
{
    for(int i = x; i < N; i += lowbit(i)) tr[i] += c;
}

int query(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        x++;  //因为x是从0开始的，而我们需要x从1开始
        res[query(x)]++;
        add(x,1);
    }
    
    for(int i = 0; i < n; ++i) printf("%d\n", res[i]);
    
    return 0;
}

二、线段树

1.概念

思想：也是用二分的策略，把一个有性质的值存在多个区间段中，然后通过下标二分来找或者修改
用途：可以快速求前缀和、区间最大值/最小值等多种用法
如下图为线段树的一个示例图：
在这里插入图片描述

2.代码模板

const int N = 1e5+10;

int n, m;
int w[N];

struct Node
{
    int l, r, sum;
}tr[N * 4];  //因为结点个数有n个，由于pushup时最底层的结点需特判，所以再开了一层

void pushup(int u)  //更新结点u
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;  //左右儿子之和
}

void build(int u, int l, int r)
{
    if(l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};  //c++11没有的默认0
        int mid = l + r >> 1;  //这里是因为底下穿的就是按mid划分的，也必须划分
        build(u << 1, l, mid), build(u << 1 | 1, mid+1, r);
        pushup(u);  //递归的过程
    }
}

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;  //相当于取包含的意思，区间是按mid已经划分好了，不重不漏
    int mid = tr[u].l + tr[u].r >> 1;  
    int sum = 0;
    if(l <= mid) sum = query(u << 1, l, r);
    if(r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v)  //给x下标加上v
{
    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);  //递归更新
    }
}

3.例题

动态求连续区间

思路：模板题

题目描述：


给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。
第二行包含 n 个整数，表示完整数列。
接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000,1≤m≤100000，1≤a≤b≤n,
数据保证在任何时候，数列中所有元素之和均在 int 范围内。

输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例：
11
30
35

示例代码：

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5+10;

int n, m;
int w[N];

struct Node
{
    int l, r, sum;
}tr[N * 4];  //因为结点个数有n个，由于pushup时最底层的结点需特判，所以再开了一层

void pushup(int u)  //更新结点u
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;  //左右儿子之和
}

void build(int u, int l, int r)
{
    if(l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};  //c++11没有的默认0
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid+1, r);
        pushup(u);  //递归的过程
    }
}

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if(l <= mid) sum = query(u << 1, l, r);
    if(r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v)  //给x下标加上v
{
    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);  //递归更新
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    
    build(1, 1, n);
    
    while(m--)
    {
        int k, a, b;
        scanf("%d%d%d", &k, &a, &b);
        if(k) modify(1, a, b);
        else printf("%d\n", query(1, a, b));
    }
    
    return 0;
}

数列区间最大值

思路：把sum变成maxv就行了，思路跟上一题是一样的。

题目描述：

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式
第一行两个整数 N,M 表示数字的个数和要询问的次数；
接下来一行为 N 个数；接下来 M 行，每行都有两个整数 X,Y。

输出格式
输出共 M 行，每行输出一个数。

数据范围
1≤N≤105,1≤M≤106,1≤X≤Y≤N,数列中的数字均不超过231−1
输入样例：
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
输出样例：
5
8

示例代码：

#include <cstdio>
#include <iostream>
#include <climits>

using namespace std;

const int N = 1e5+10;

int n, m;
int w[N];

struct Node
{
    int l, r, maxv;
}tr[N * 4];

void pushup(int u)
{
    tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
}

void build(int u, int l, int r)
{
    if(l == r) tr[u] = {l,r,w[r]};
    else
    {
        tr[u] = {l,r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid+1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;
    int maxv = INT_MIN;
    if(l <= mid) maxv = query(u << 1, l, r);
    if(r > mid) maxv = max(maxv, query(u << 1 | 1, l, r));
    return maxv;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    
    build(1,1,n);
    
    while(m--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", query(1,a,b));
    }
    
    return 0;
}