二叉树OJ题（2）——二叉树的四种遍历

news2025/1/11 12:45:44

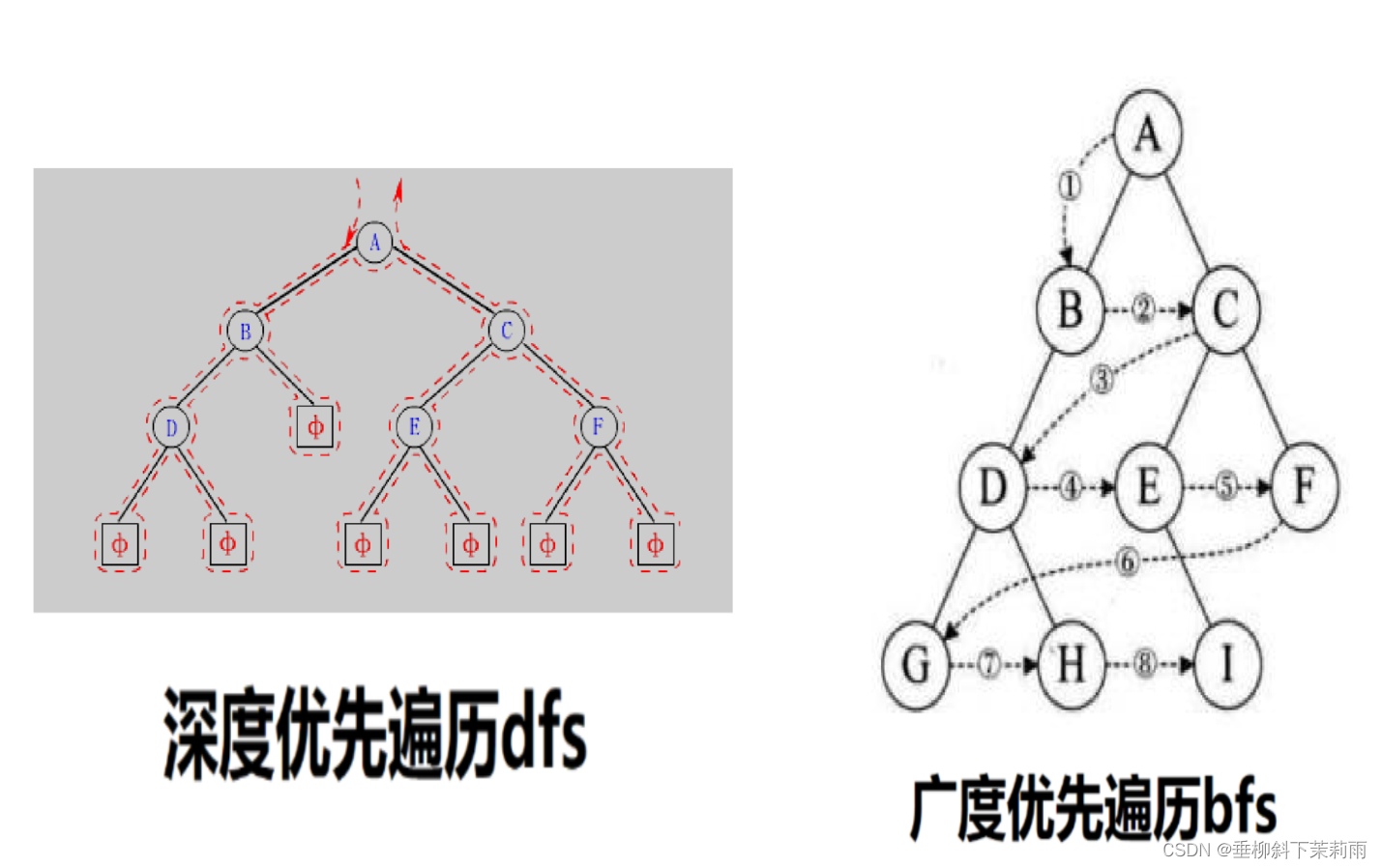
前序 -> 深度优先遍历dfs

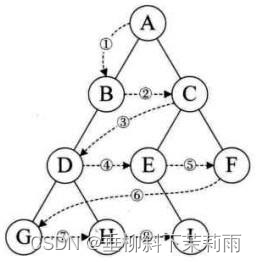
层序 -> 广度优先遍历bfs

6 二叉树的前序遍历

OJ链接

思路分析

开辟一个数组，然后把前序遍历树的顺序放入数组即可。

把根的val放入数组第一个元素
接着放入左右（递归下去）

代码实现

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}
 
int *preorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
    a[(*pi)++]=root->val;
    preorder(root->left,a,pi);
    preorder(root->right,a,pi);
    return a;
}
 
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    //注意这里传地址
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=preorder(root,a,&i);
    i=0;
    return a;
}

注意事项

改变形式参数必须要用指针，形参的修改不影响实参，形参是实参的一份临时拷贝。
一定要注意这里要是 int* pi，pi在不同函数里调用的时候是形式参数，使用时需要用指针才行。（也可以使用全局变量，int i。但是一定要在preorderTraversal函数里调用preorder函数递归前将i置零，因为外界可能会多次调用preorderTraversal函数，就会造成越界！）
👇错误案例

7 二叉树的中序遍历

OJ链接

代码实现

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}
 
int *inorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
    inorder(root->left,a,pi);
    a[(*pi)++]=root->val;
    inorder(root->right,a,pi);
    return a;
}
 
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=inorder(root,a,&i);
    i=0;
    return a;
}

8 二叉树的后序遍历

OJ链接

代码实现

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}
 
int *postorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
    postorder(root->left,a,pi);//
    postorder(root->right,a,pi);
    a[(*pi)++]=root->val;//
    return a;
}
 
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=postorder(root,a,&i);
    i=0;
    return a;
}

9 层序遍历

层序遍历的概念

层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。

设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

层序遍历的实现

层序遍历的实现需要用到队列，回顾👉单链表实现队列

整体思路

首先把根入队列
然后保存根节点，遍历打印根节点，
把根节点的左右孩子入队列（父亲出的时候就入父亲的左右孩子）
根节点出队列

代码实现

void LevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
        //注意这里传的是地址，而不是值！！！
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);

		printf("%d ", front->data);

		if (front->left)
			QueuePush(&q, front->left);

		if (front->right)
			QueuePush(&q, front->right);
	}
    printf("\n");

	QueueDestroy(&q);
}

int main()
{
	TreeNode* root = CreateTree();
	LevelOrder(root);

	DestoryTree(root);
	root = NULL;

	return 0;
}

图示理解

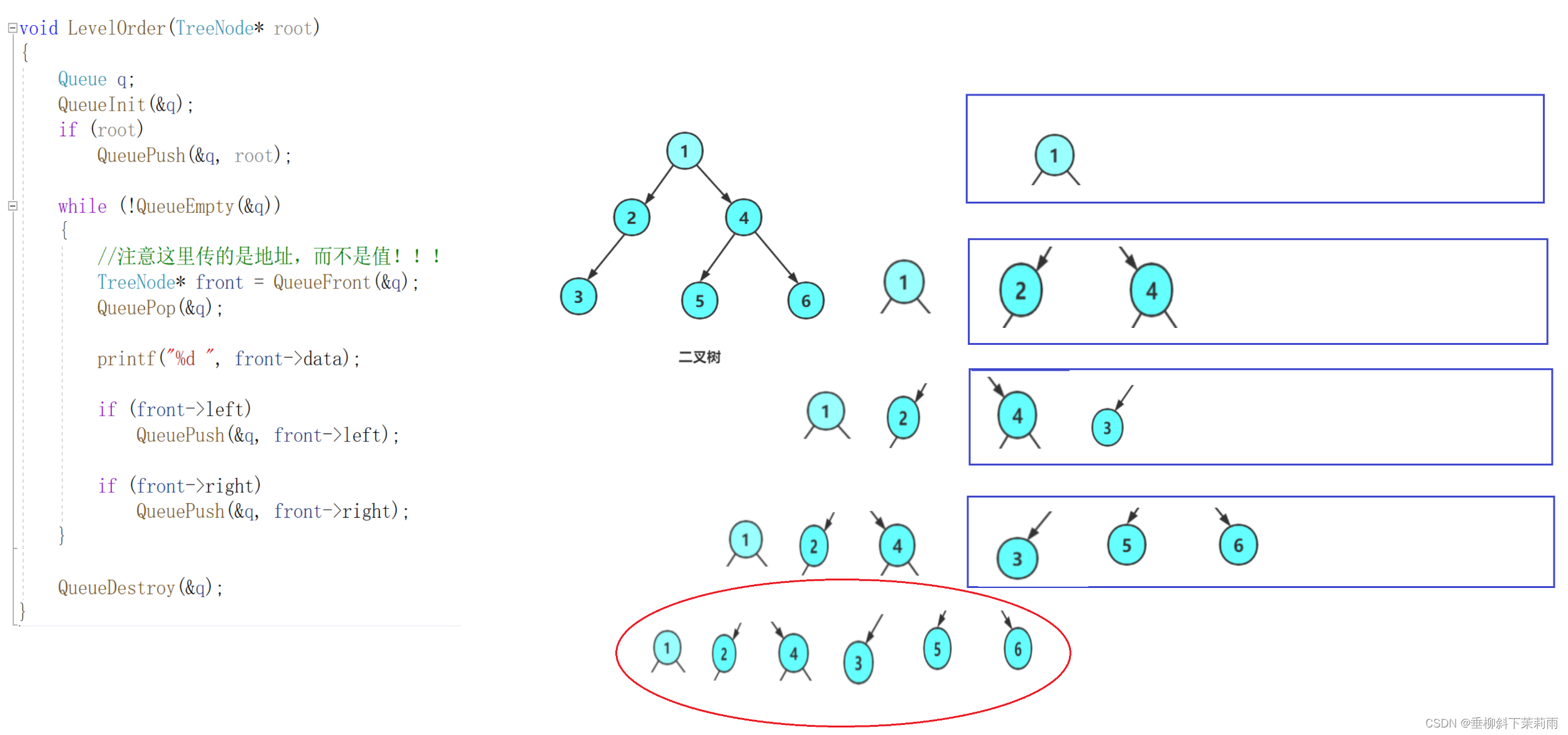
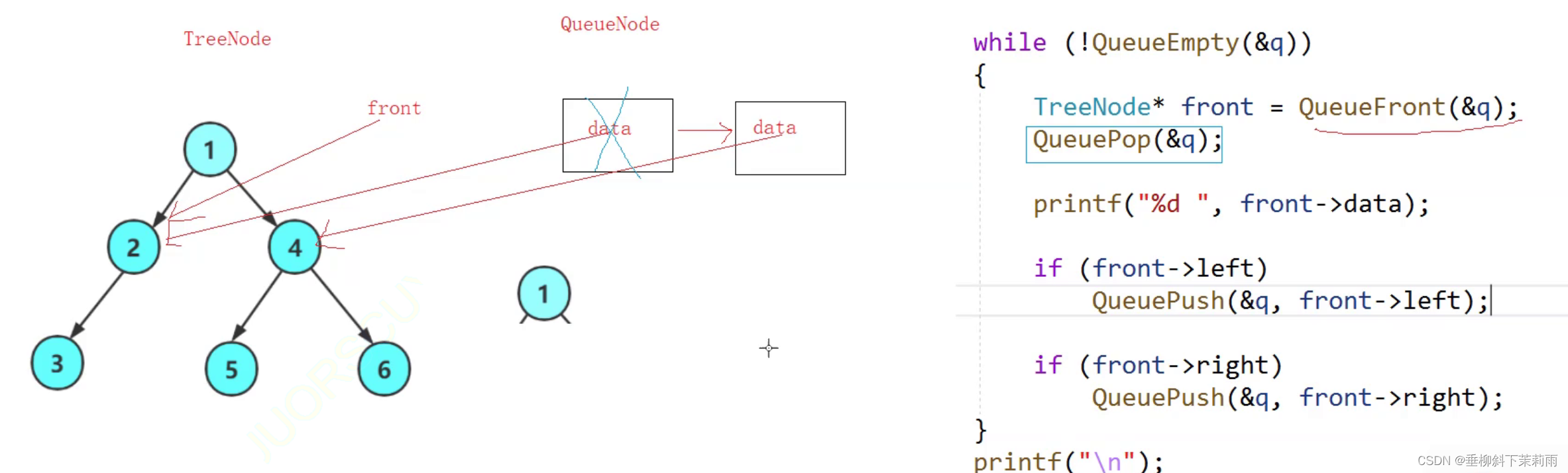
问：为什么我们已经把节点给Pop了，但是后面却还能用front呢？

注意这里free的是QueueNode的节点，而非TreeNode的！！

变形

如果想要一层一层输出，代码应该怎么改？

设置一个变量LeveSize记录每层的个数，控制一层一层出队列。

代码实现

void LevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	int levelSize = 1;
	while (!QueueEmpty(&q))
	{
		// 一层一层出
		while (levelSize--)
		{
			TreeNode* front = QueueFront(&q);
			QueuePop(&q);

			printf("%d ", front->data);

			if (front->left)
				QueuePush(&q, front->left);

			if (front->right)
				QueuePush(&q, front->right);
		}
		printf("\n");

		levelSize = QueueSize(&q);
	}
	printf("\n");
	QueueDestroy(&q);
}