Kalman滤波是一种用于估计系统状态的优秀滤波方法,特别适用于具有噪声的测量数据的情况。它的主要应用包括导航、目标跟踪、信号处理、机器人技术等领域。Kalman滤波器通过融合系统模型和实际测量数据,提供对系统状态的最优估计。
Kalman滤波器的原理基于两个主要步骤:预测和更新。
-
预测步骤(预测状态):
- 根据系统的动态模型,通过先前的状态估计预测当前时刻的状态。
- 预测系统状态的不确定性(协方差矩阵)。
-
更新步骤(融合测量数据):
- 获取实际的测量数据。
- 计算预测状态与测量数据之间的残差(残差是预测值和测量值的差异)。
- 根据残差和预测状态的不确定性,更新系统状态的估计值和不确定性。
Matlab中可以使用以下代码来演示一个简单的一维Kalman滤波器的应用:
% 定义系统参数
A = 1; % 状态转移矩阵
H = 1; % 测量矩阵
Q = 0.01; % 系统过程噪声的方差
R = 0.1; % 测量噪声的方差
% 初始化状态估计和不确定性
x_hat = 0;
P = 1;
% 模拟系统状态和测量数据
true_state = sin(0.1:0.1:10); % 实际系统状态
measurements = true_state + sqrt(R) * randn(size(true_state)); % 加入测量噪声
% Kalman滤波
filtered_state = zeros(size(true_state));
for k = 1:length(true_state)
% 预测步骤
x_hat_minus = A * x_hat;
P_minus = A * P * A' + Q;
% 更新步骤
K = P_minus * H' / (H * P_minus * H' + R);
x_hat = x_hat_minus + K * (measurements(k) - H * x_hat_minus);
P = (1 - K * H) * P_minus;
% 保存滤波后的状态估计值
filtered_state(k) = x_hat;
end
% 绘制结果
figure;
plot(0.1:0.1:10, true_state, '-g', 0.1:0.1:10, measurements, 'or', 0.1:0.1:10, filtered_state, '-b');
legend('True State', 'Measurements', 'Filtered State');
xlabel('Time');
ylabel('Value');
title('Kalman Filter Demo');
结果如下:
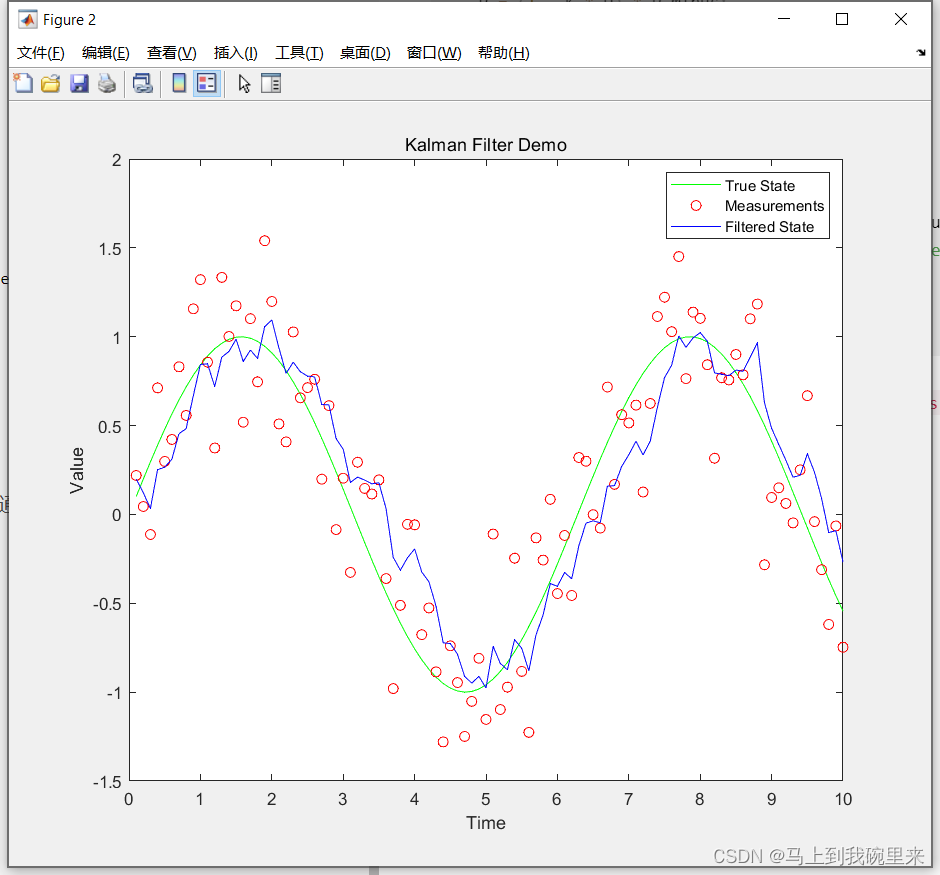
此示例中,true_state表示实际系统状态,measurements表示带有噪声的测量数据。Kalman滤波器通过不断预测和更新,提供了对系统状态的估计,最终在图中用蓝色曲线表示。
在上面的Matlab示例中,观测量由以下语句生成:
measurements = true_state + sqrt(R) * randn(size(true_state));
这行代码使用了正弦波形true_state作为实际系统状态,并添加了服从正态分布的测量噪声。具体而言,sqrt(R) * randn(size(true_state))生成了一个与true_state相同大小的正态分布随机数列,其中sqrt(R)表示噪声的标准差。
这样生成的measurements就代表了在实际系统状态上加入了测量噪声的观测量。在Kalman滤波器中,这些观测量将用于更新状态估计,以提高对系统真实状态的估计准确性。