René Descartes
一、笛卡尔(René Descartes)
勒内·笛卡尔(René Descartes,1596年3月31日-1650年2月11日),1596年3月31日生于法国安德尔-卢瓦尔省的图赖讷(现笛卡尔,因笛卡尔得名),1650年2月11日逝于瑞典斯德哥尔摩,法国哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化而被认为是解析几何之父。
他还是西方现代哲学思想的奠基人之一,是近代唯心论的开拓者,提出了“普遍怀疑”的主张。他的哲学思想深深影响了之后的几代欧洲人,并为欧洲的“理性主义”哲学奠定了基础。
笛卡尔最为世人熟知的是其作为数学家的成就。他于1637年发明了现代数学的基础工具之一——坐标系,将几何和代数相结合,创立了解析几何学。同时,他也推导出了笛卡尔定理等几何学公式。值得一提的是,传说著名的心形线方程也是由笛卡尔提出的。
在哲学上,笛卡尔是一个二元论者以及理性主义者。他是欧陆“理性主义”的先驱。关于笛卡尔的哲学思想,最著名的就是他那句“我思故我在 ”。他的《第一哲学沉思集》(又名《形而上学的沉思》)仍然是许多大学哲学系的必读书目之一。
在物理学方面,笛卡尔将其坐标几何学应用到光学研究上,在《屈光学》中第一次对折射定律作出了理论上的推证。在他的《哲学原理》第二章中以第一和第二自然定律的形式首次比较完整地表述了惯性定律,并首次明确地提出了动量守恒定律。这些都为后来牛顿等人的研究奠定了一定的基础。
二、笛卡尔树(Cartesian Tree)
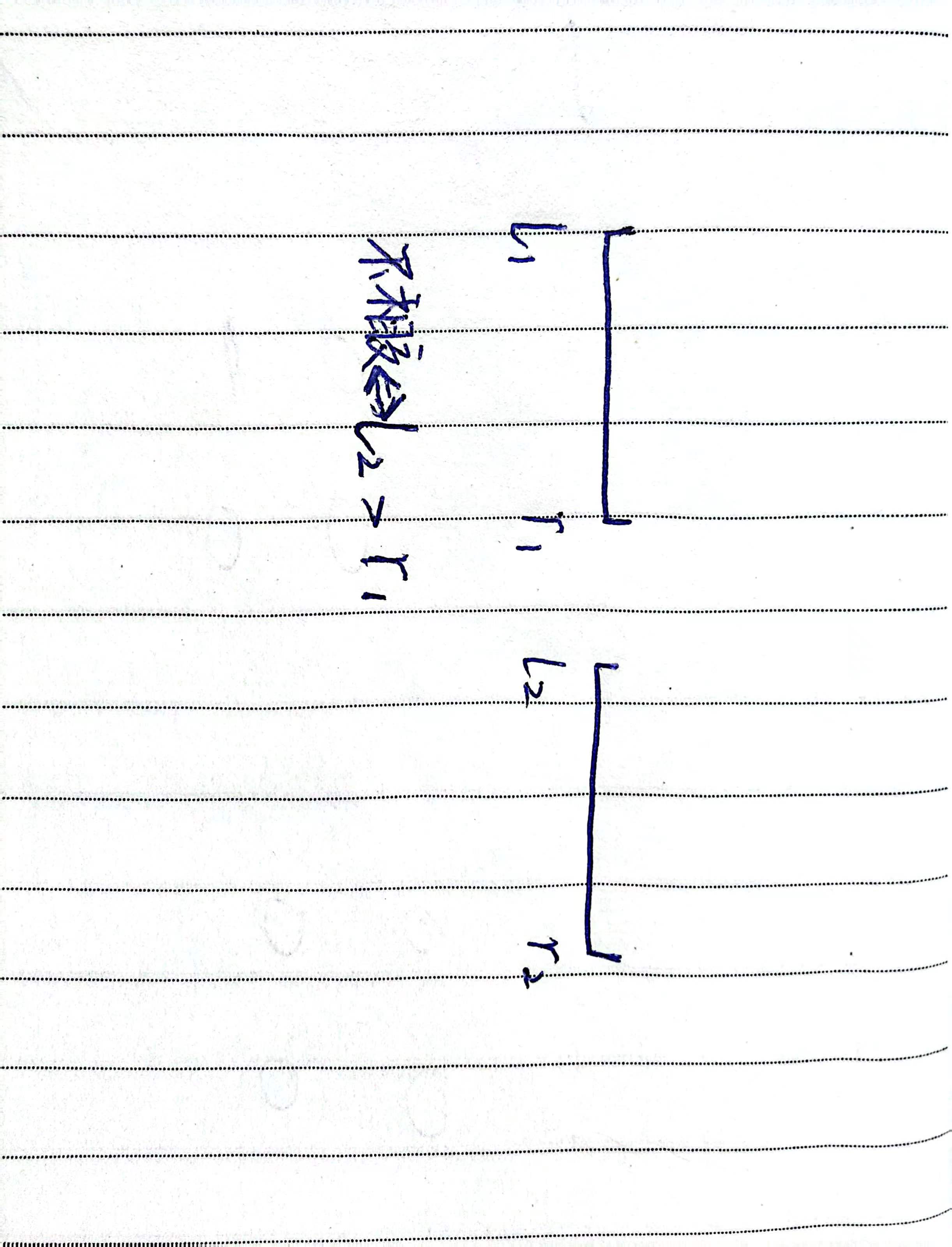
笛卡尔树是一种特定的二叉树数据结构,可由数列构造,
在范围最值查询、范围top k查询(range top k queries)等问题上有广泛应用。

using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Algorithm_Gallery
{
/// <summary>
/// 遍历结果
/// </summary>
public static List<string> Traversal_Result = new List<string>();
/// <summary>
/// In-Order遍历
/// </summary>
/// <param name="node"></param>
public static void Cartesian_Tree_Inorder_Traversal(BinaryNode node)
{
if (node == null)
{
return;
}
Cartesian_Tree_Inorder_Traversal(node.Left);
//Console.Write(node.Data + " ");
Traversal_Result.Add(node.Data);
Cartesian_Tree_Inorder_Traversal(node.Right);
}
private static BinaryNode Cartesian_Tree_Utility(int root, int[] arr, int[] parent, int[] leftchild, int[] rightchild)
{
if (root == -1)
{
return null;
}
BinaryNode temp = new BinaryNode(arr[root]);
temp.Left = Cartesian_Tree_Utility(leftchild[root], arr, parent, leftchild, rightchild);
temp.Right = Cartesian_Tree_Utility(rightchild[root], arr, parent, leftchild, rightchild);
return temp;
}
// A function to create the Cartesian Tree in O(N) time
/// <summary>
/// 创建笛卡尔树
/// </summary>
/// <param name="arr"></param>
/// <param name="n"></param>
/// <returns></returns>
public static BinaryNode Cartesian_Tree_Growth(int[] arr, int n)
{
int[] parent = new int[n];
int[] leftchild = new int[n];
int[] rightchild = new int[n];
Array_Initialize(parent, -1);
Array_Initialize(leftchild, -1);
Array_Initialize(rightchild, -1);
int root = 0, last;
for (int i = 1; i <= n - 1; i++)
{
last = i - 1;
rightchild[i] = -1;
while (arr[last] <= arr[i] && last != root)
{
last = parent[last];
}
if (arr[last] <= arr[i])
{
parent[root] = i;
leftchild[i] = root;
root = i;
}
else if (rightchild[last] == -1)
{
rightchild[last] = i;
parent[i] = last;
leftchild[i] = -1;
}
else
{
parent[rightchild[last]] = i;
leftchild[i] = rightchild[last];
rightchild[last] = i;
parent[i] = last;
}
}
parent[root] = -1;
return (Cartesian_Tree_Utility(root, arr, parent, leftchild, rightchild));
}
private static void Array_Initialize(int[] arr, int value)
{
for (int i = 0; i < arr.Length; i++)
{
arr[i] = value;
}
}
}
}