题目链接

D. In Love

题意

线段的集合，有两种操作

1. 插入一个线段
2. 删除一个线段
   每次操作后都要去查询是否存在两个线段不相交

题解

首先先看两个线段不相交需要满足什么条件

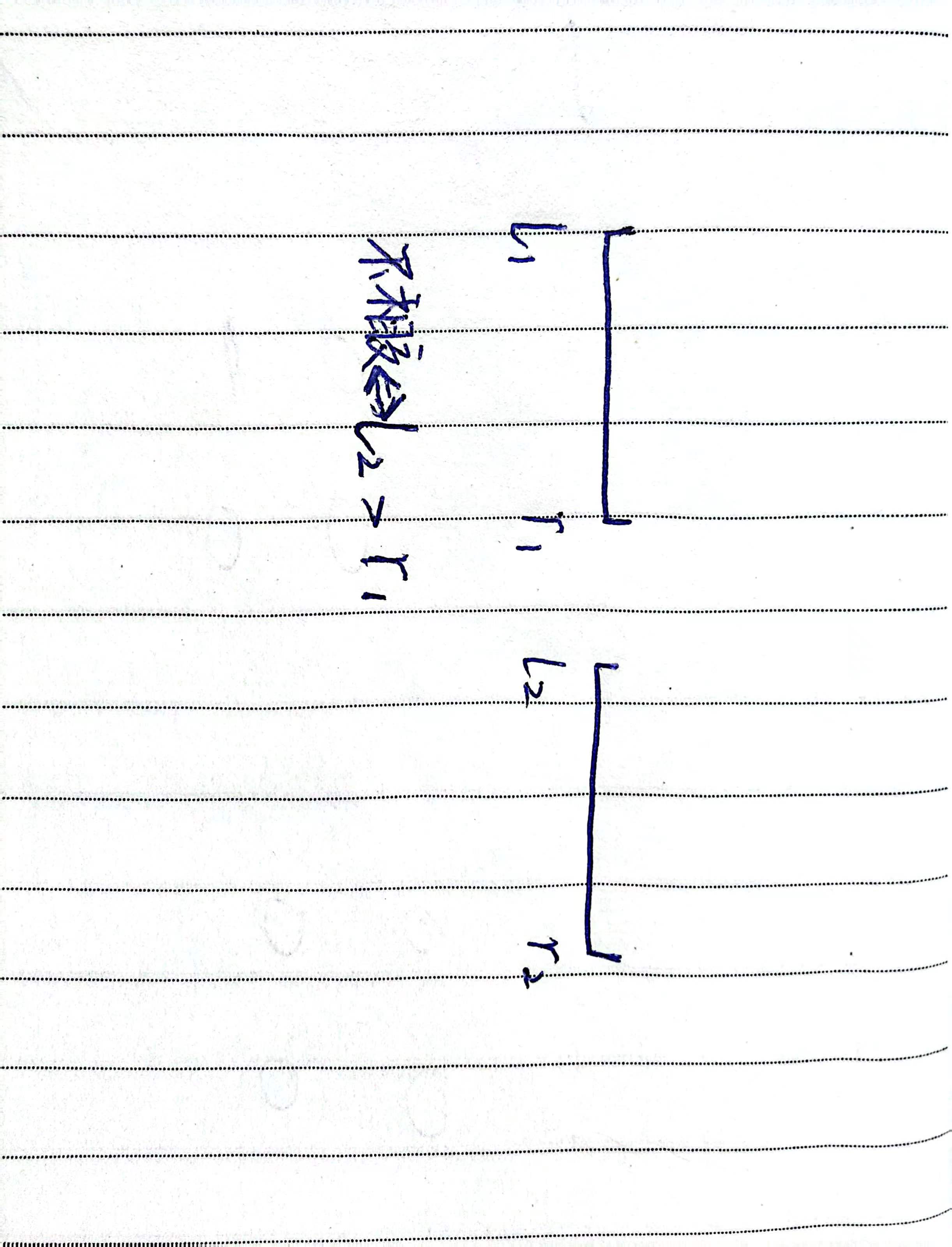
也就是较$大l>小r$即可满足不相交
我们进行推广
当集合中，最大的$l>$最小的$r$时就存在区间不相交
注意是严格大于。
这样我们只需要维护两个集合，左端点的集合和右端点的集合，然后每次查询集合中的最值。
$set$和$multiset$都可以完成这件事，这道题目里面区间可能重复，所以用$multiset$去维护最大值最小值即可。

代码

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back

using namespace std;

void solve() {
	int q;
	cin>>q;
	
	multiset<int>sl,sr;
	while(q--){
		char op;
		cin>>op;
		int l,r;
		cin>>l>>r;
		if(op=='+'){
			sl.insert(l);
			sr.insert(r);
		}else{
			sl.erase(sl.find(l));
			sr.erase(sr.find(r));
		}
		if(sl.size()<=1||sr.size()<=1){
			cout<<"NO"<<endl;
			continue;
		}
		int d=(*sl.rbegin())-(*sr.begin());
		if(d>0){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

总结

1. 区间不相交的充要条件
2. multiset的erase用法
   不小心就用错了，erase可以传入迭代器的位置，也可以传入要删除的值，如果在set里面这两个都可以，在multiset里面一个值可能出现多次，如果传入值，就会把这所有数都删除，如果只想删除一个，可以先用find函数得到一个迭代器的位置再删除