OSQP文档学习

news2025/1/18 7:31:19

OSQP官方文档

1 QSQP简介

OSQP求解形式为的凸二次规划：
在这里插入图片描述
$x∈R^n$ ：优化变量
$P∈S^n_+$ ：半正定矩阵

特征
（1）高效：使用了一种自定义的基于ADMM的一阶方法，只需要在设置阶段进行单个矩阵分解。
（2）鲁棒：该算法设置之后不需要对问题数据进行假设（问题只需要是凸的）。
（3）原始/对偶不可行问题：当问题是原始或对偶不可行时，OSQP会检测到它。这是第一个基于一阶方法的QP求解器。
（4）可嵌入：有一个简单的接口来生成定制的可嵌入C代码，而不需要内存管理器。
（5）不需要外部库即可运行
（6）可以很容易地进行热启动，并且可以缓存矩阵分解，以非常有效地解决参数化问题
（7）接口：提供了到C、C++、Fortran、Julia、Matlab、Python、R、Ruby和Rust的接口

2 OSQP求解器

在这里插入图片描述
求解器运行以下ADMM算法：

$\Pi$ ：投影到超盒上 $[l, u]$ ， $\rho$ 是ADMM步长
Linear system solution
线性系统解是算法的核心部分。它可以使用直接或间接的方法来完成。
使用直接线性系统求解器，我们求解以下具有拟定矩阵的线性系统：
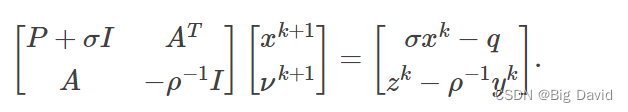
在这里插入图片描述
使用间接线性系统求解器，我们求解以下具有正定矩阵的线性系统：

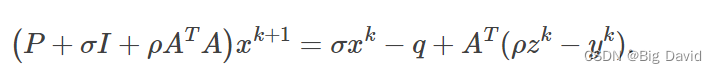
OSQP核心旨在支持不同的线性系统求解器。

Convergence
在每k次迭代时，OSQP生成一个元组 $x^k,z^k,y^k)$ ，
$x^k∈R^n,z^k、y^k∈R^m$
与 $x^k,z^k,y^k)$ 相关的原始残差和对偶残差：
在这里插入图片描述

#pic
不可行问题
OSQP能够检测问题是原始不可行还是对偶不可行。

3 Get started

安装：
Linux操作系统，默认gcc,cmake已经安装好
① 克隆存储库

git clone https://github.com/osqp/osqp

cd osqp
mkdir build
cd build

③ 创建 Makefile

cmake -G "Unix Makefiles" ..

④ 编译 OSQP

cmake --build .

C语言：
在 CMake 项目中包括 OSQP，具体取决于您需要共享库还是静态库：

# Find OSQP library and headers
find_package(osqp REQUIRED)

# Link the OSQP shared library
target_link_libraries(yourTarget PRIVATE osqp::osqp)

# or...

# Link the OSQP static library
target_link_libraries(yourTarget PRIVATE osqp::osqpstatic)

4 接口

OSQP有几个接口。以下链接中显示了有关设置、状态值以及如何指定不同线性系统解算器的信息
Solver settings
Linear Systems Solvers
Status values

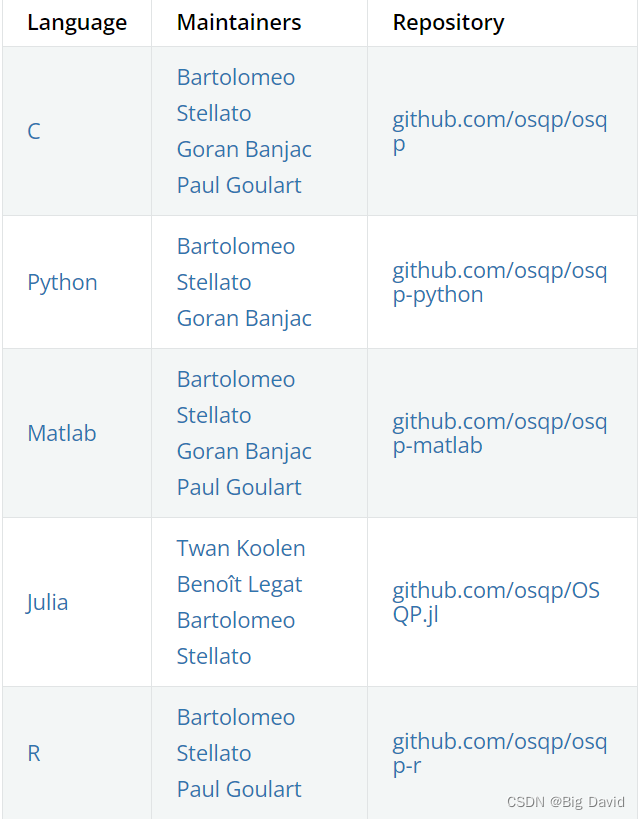
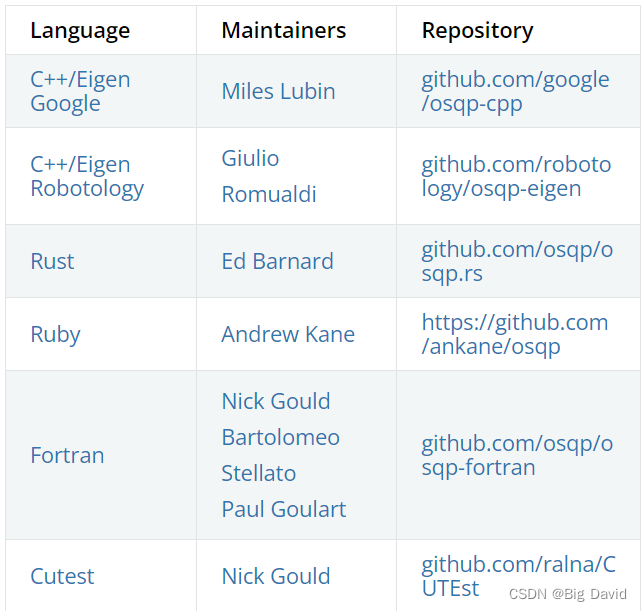
在这里插入图片描述

C：github.com/osqp/osqp
C++：github.com/robotology/osqp-eigen

5 Examples

Demo:
① Setup and solve ：设置和求解
在这里插入图片描述
C:

#include <stdlib.h>
#include "osqp.h"

int main(int argc, char **argv) {
    /* Load problem data */
    OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };
    OSQPInt P_nnz = 3;
    OSQPInt P_i[3] = {0, 0, 1, };
    OSQPInt P_p[3] = {0, 1, 3, };
    OSQPFloat q[2] = {1.0, 1.0, };
    OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };
    OSQPInt A_nnz = 4;
    OSQPInt A_i[4] = {0, 1, 0, 2, };
    OSQPInt A_p[3] = {0, 2, 4, };
    OSQPFloat l[3] = {1.0, 0.0, 0.0, };
    OSQPFloat u[3] = {1.0, 0.7, 0.7, };
    OSQPInt n = 2;
    OSQPInt m = 3;

    /* Exitflag */
    OSQPInt exitflag = 0;

    /* Solver, settings, matrices */
    OSQPSolver   *solver;
    OSQPSettings *settings;
    OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));
    OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));

    /* Populate matrices */
    csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);
    csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);

    /* Set default settings */
    settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));
    if (settings) {
        osqp_set_default_settings(settings);
        settings->alpha = 1.0; /* Change alpha parameter */
    }

    /* Setup solver */
    exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);

    /* Solve problem */
    if (!exitflag) exitflag = osqp_solve(solver);

    /* Cleanup */
    osqp_cleanup(solver);
    if (A) free(A);
    if (P) free(P);
    if (settings) free(settings);

    return (int)exitflag;
};

② Update vectors：更新向量
在这里插入图片描述

#include <stdlib.h>
#include "osqp.h"

int main(int argc, char **argv) {
    /* Load problem data */
    OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };
    OSQPInt P_nnz = 3;
    OSQPInt P_i[3] = {0, 0, 1, };
    OSQPInt P_p[3] = {0, 1, 3, };
    OSQPFloat q[2] = {1.0, 1.0, };
    OSQPFloat q_new[2] = {2.0, 3.0, };
    OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };
    OSQPInt A_nnz = 4;
    OSQPInt A_i[4] = {0, 1, 0, 2, };
    OSQPInt A_p[3] = {0, 2, 4, };
    OSQPFloat l[3] = {1.0, 0.0, 0.0, };
    OSQPFloat l_new[3] = {2.0, -1.0, -1.0, };
    OSQPFloat u[3] = {1.0, 0.7, 0.7, };
    OSQPFloat u_new[3] = {2.0, 2.5, 2.5, };
    OSQPInt n = 2;
    OSQPInt m = 3;

    /* Exitflag */
    OSQPInt exitflag = 0;

    /* Solver, settings, matrices */
    OSQPSolver   *solver;
    OSQPSettings *settings;
    OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));
    OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));

    /* Populate matrices */
    csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);
    csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);

    /* Set default settings */
    settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));
    if (settings) osqp_set_default_settings(settings);

    /* Setup solver */
    exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);

    /* Solve problem */
    if (!exitflag) exitflag = osqp_solve(solver);

    /* Update problem */
    if (!exitflag) exitflag = osqp_update_data_vec(solver, q_new, l_new, u_new);

    /* Solve updated problem */
    if (!exitflag) exitflag = osqp_solve(work);

    /* Cleanup */
    osqp_cleanup(solver);
    if (A) free(A);
    if (P) free(P);
    if (settings) free(settings);

    return (int)exitflag;
};

③ Update matrices：更新矩阵P和A
在这里插入图片描述

#include <stdlib.h>
#include "osqp.h"

int main(int argc, char **argv) {
    /* Load problem data */
    OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };
    OSQPFloat P_x_new[3] = {5.0, 1.5, 1.0, };
    OSQPInt P_nnz = 3;
    OSQPInt P_i[3] = {0, 0, 1, };
    OSQPInt P_p[3] = {0, 1, 3, };
    OSQPFloat q[2] = {1.0, 1.0, };
    OSQPFloat q_new[2] = {2.0, 3.0, };
    OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };
    OSQPFloat A_x_new[4] = {1.2, 1.5, 1.1, 0.8, };
    OSQPInt A_nnz = 4;
    OSQPInt A_i[4] = {0, 1, 0, 2, };
    OSQPInt A_p[3] = {0, 2, 4, };
    OSQPFloat l[3] = {1.0, 0.0, 0.0, };
    OSQPFloat l_new[3] = {2.0, -1.0, -1.0, };
    OSQPFloat u[3] = {1.0, 0.7, 0.7, };
    OSQPFloat u_new[3] = {2.0, 2.5, 2.5, };
    OSQPInt n = 2;
    OSQPInt m = 3;

    /* Exitflag */
    OSQPInt exitflag = 0;

    /* Solver, settings, matrices */
    OSQPSolver   *solver;
    OSQPSettings *settings;
    OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));
    OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));

    /* Populate matrices */
    csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);
    csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);

    /* Set default settings */
    settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));
    if (settings) osqp_set_default_settings(settings);

    /* Setup solver */
    exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);

    /* Solve problem */
    if (!exitflag) exitflag = osqp_solve(solver);

    /*  Update problem
        NB: Update only upper triangular part of P
     */
    if (!exitflag) exitflag = osqp_update_data_mat(solver,
                                                   P_x_new, OSQP_NULL, 3,
                                                   A_x_new, OSQP_NULL, 4);

    /* Solve updated problem */
    if (!exitflag) exitflag = osqp_solve(work);

    /* Cleanup */
    osqp_cleanup(solver);
    if (A) free(A);
    if (P) free(P);
    if (settings) free(settings);

    return (int)exitflag;
};

应用：
① Huber fitting
② Lasso
③ Least-squares：最小二乘法
④ Model predictive control (MPC)
我们考虑将线性时不变动力系统控制到某个参考状态的问题。为了实现这一点，我们使用约束线性二次 MPC，它在每个时间步长求解以下有限视界最优控制问题 $x_r∈R^{n_x}$
在这里插入图片描述