平台:Vivado2018.3.
芯片:xcku115-flva1517-2-i (active)
最近学习使用了xilinx除法器,在使用过程中出现了很多次除法器的结果和我预计的结果不一致,特此记录学习一下。
参考文件:pg151.下载地址
pg151-div-gen.pdf • 查看器 • AMD 自适应计算文档门户 (xilinx.com)
IP配置说明

Xilinx除法器拥有三种模式
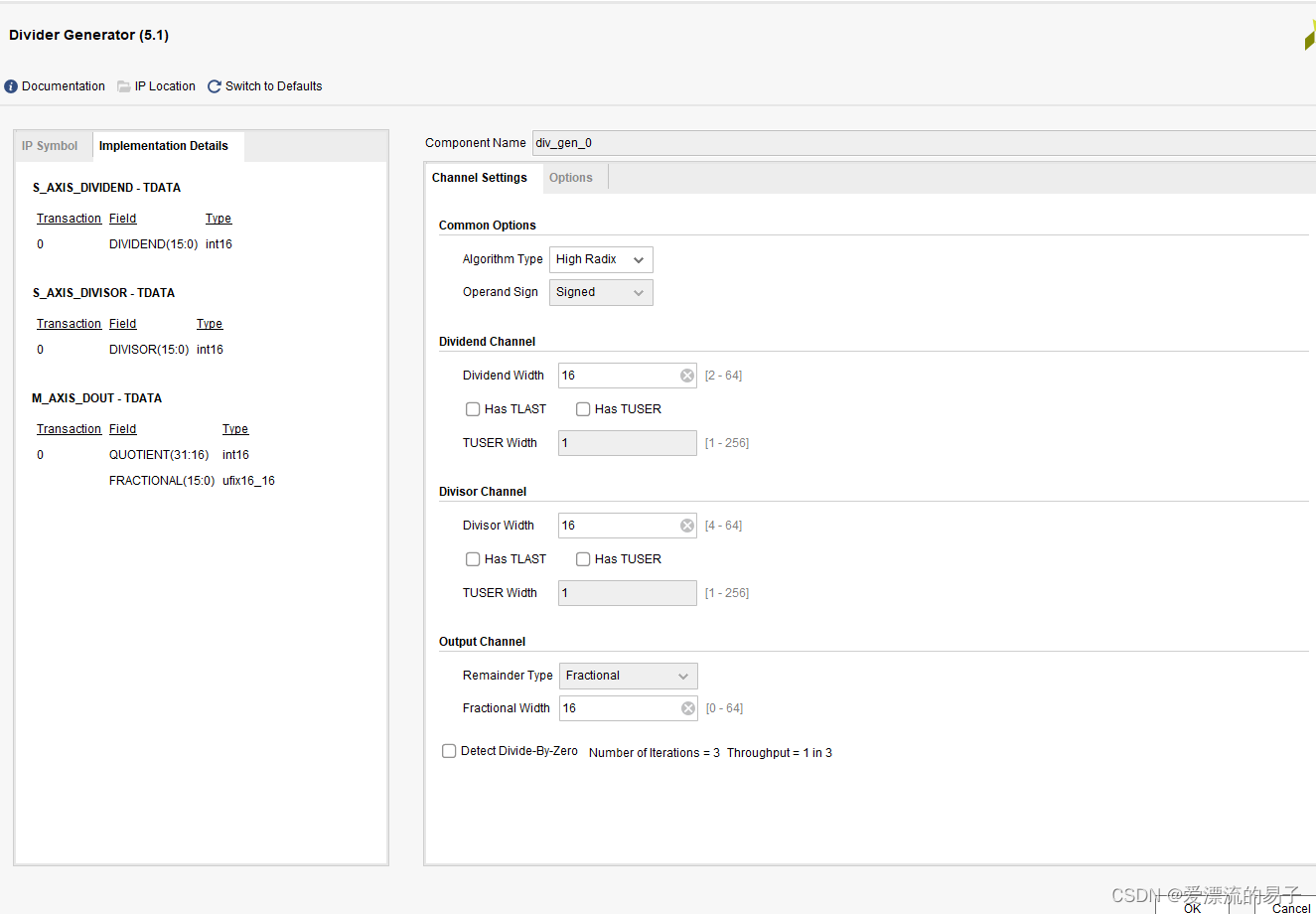
Radix2: The implementation uses FPGA logic primitives (registers and LUTs). The Radix2 solution does not use DSP or block RAM primitives.使用FPGA寄存器和LUT资源,不使用dsp和ram资源。被除数位宽2-64,除数位宽2-64。支持无符号或二进制补码有符号数。结果可以配置为商和余数,商和小数。
High radix:该实现使用DSP切片和块RAM。被除数位宽2-64,除数位宽2-64。支持有符号数。结果可以配置为商和小数。
Lutmult:使用了DSP,RAM,以及LutMult资源。被除数位宽2-17,除数位宽2-17(被除数和除数位宽之和限制在23位以内)支持无符号或二进制补码有符号数。结果为商和余数。
在学习此IP之前,需要先复习一下二进制数的表示。
1、 无符号二进制数据unsigned。
无符号数据。例如8位无符号数就代表的十进制数的范围为[0,2^n-1]。
2、 有符号的二进制数据的表示signed。
有符号数据。除数据位外最高位代表符号位。例如8位的有符号数据的数值范围为[-128,127]。我们知道计算机中的数据都是用补码来参与运算。那么计算机里面为何要使用补码来计算呢?计算机中使用补码就可以将原本的减法转换为加法运算。
例如
1,二进制补码为00000001.(代表无符号数为1)
-1,二进制补码为11111111.(代表无符号数为255)
-2,二进制补码为11111110.(代表无符号数为254)
计算机计算
1+(-1),即1+255=256,(100000000),低8位就是0的补码00000000
-1+(-2),及255+254=509,(111111101),低八位就是-3的补码11111101
是不是很方便,所有的减法运算都改变成了加法运算。
Dividend channel被除数,
Divisor channel除数
Output channel
Remander type:
remainder余数模式。
Fractional小数模式。
Fractional width小数位宽

设置IP的模式。和输出延时。
对该IP仿真。
仿真tb
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2024/02/04 16:05:55
// Design Name:
// Module Name: vtf_div_top
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
module vtf_div_top;
reg signed[15:0] dividend_tdata ;
reg dividend_tvalid ;
reg signed[15:0] divisor_tdata ;
reg divisor_tvalid ;
//
reg clk ;
reg rst_n ;
div_top div_top(
//
.dividend_tdata (dividend_tdata ),
.dividend_tvalid (dividend_tvalid ),
.divisor_tdata (divisor_tdata ),
.divisor_tvalid (divisor_tvalid ),
//
.clk (clk ),
.rst_n (rst_n )
);
//------------------------------------------------------
//复位参数
//------------------------------------------------------
integer i;
//设置复位参数
initial
begin
$display("[%t] : reset begin...", $realtime);
rst_n = 0;
for( i=0 ; i<100 ; i=i+1)
begin
@(posedge clk );
end
$display("[%t] : reset stop...", $realtime);
rst_n = 1;
end
parameter delay_cnt = 500;
reg [15:0] data_value;
reg data_en;
reg delay_over;
//------------------------------------------------------
initial
begin
clk = 0;
dividend_tdata =0;
divisor_tdata =0;
dividend_tvalid =0;
divisor_tvalid =0;
wait(rst_n == 1);
$display("[%t] : div start...", $realtime);
delay(delay_over,delay_cnt);//调用等待任务
//------------------------------------------------------
//调任务
data_gen(data_value,16'd10);//产生被除数
dividend_tdata = data_value;
data_gen(data_value,16'd3);//产生除数
// data_gen(data_value,-16'd3);//产生除数
divisor_tdata = data_value;
data_valid(data_en);
dividend_tvalid = data_en;
divisor_tvalid = data_en;
data_uvalid(data_en);
dividend_tvalid = data_en;
divisor_tvalid = data_en;
delay(delay_over,delay_cnt);//调用等待任务
$display("[%t] : div end...", $realtime);
$finish(2);
end
//------------------------------------------------------
//任务,输出一个数据
//------------------------------------------------------
task data_gen;
output [15:0] data_out;
input [15:0] data_in;
begin
data_out = data_in;
end
endtask
//------------------------------------------------------
//任务,数据有效
//------------------------------------------------------
task data_valid;
output data_en;
begin
repeat(1)@(posedge clk);
data_en = 1;
end
endtask
//------------------------------------------------------
//任务,数据无效
//------------------------------------------------------
task data_uvalid;
output data_en;
begin
repeat(1)@(posedge clk);
data_en = 0;
end
endtask
//------------------------------------------------------
//任务,延时模块
//------------------------------------------------------
task delay;
output delay_over;
input [31:0] delay_in;
begin
repeat(delay_in)@(posedge clk);
delay_over = 1;
end
endtask
always#5 clk = ~clk;
endmodule
余数模式
10/-3=-3余数为1
整数位为-3,余数位1
小数模式
10/3≈3.333333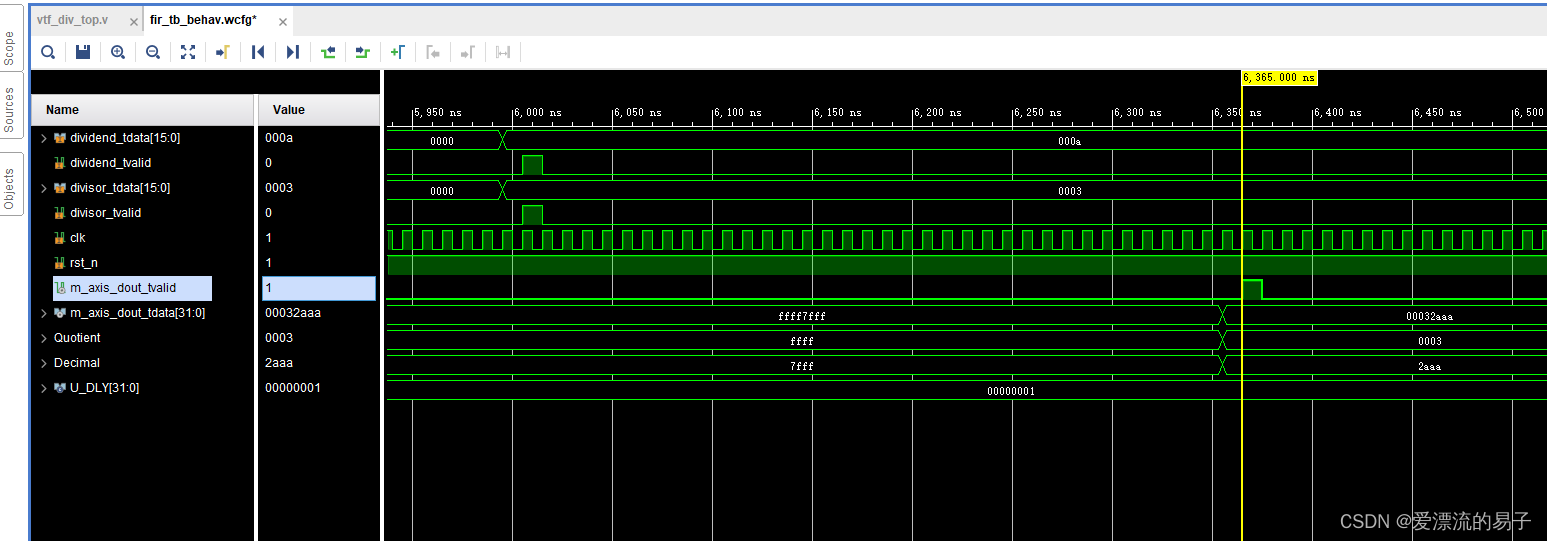
输出的小数将量化到2^15次方上。最高位表示符号位。
3.3333333
整数位为高16位。为fffd,代表-3
小数0.333333量化到2^15次方为10,922。
小数位为低16位。为2aaa(10922),还原回去0.3333129,有量化误差。原因为量化位宽为15位。
10/-3≈-3.333333
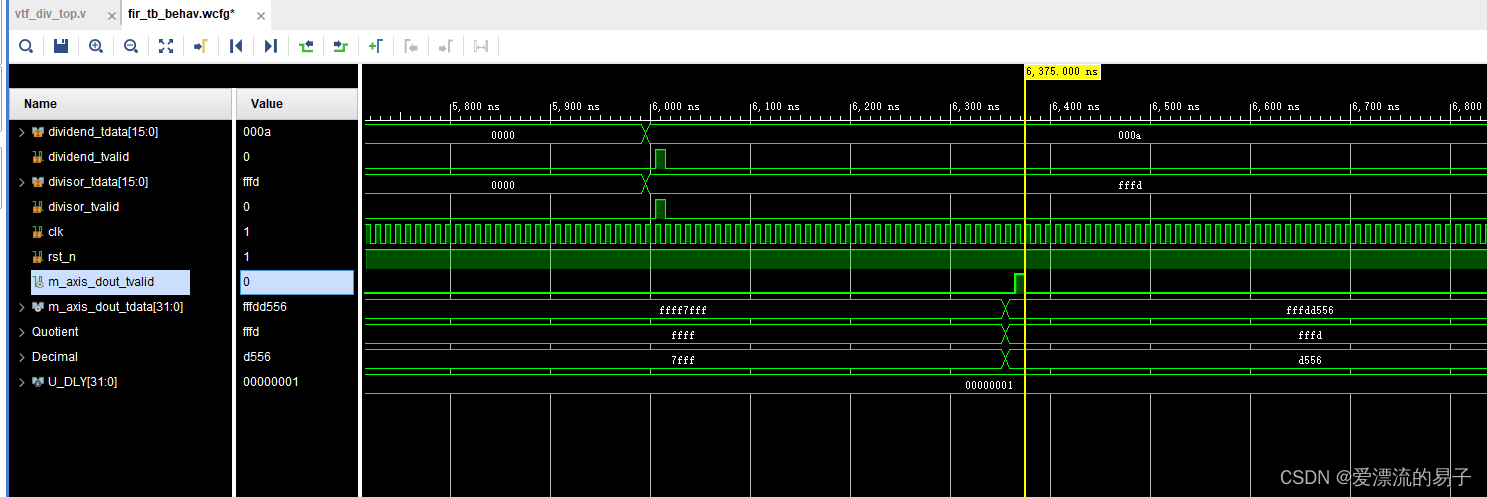
输出的小数将量化到2^15次方上。最高位表示符号位。
-3.3333333
整数位为高16位。为fffd,代表-3
小数-0.333333量化到2^15次方为-10,922。
小数位为低16位。为d556(-10922),还原回去-0.3333129。
值得注意的是当IP的模式High radix时。
小数表示已经没有了最高位的符号位。会将得到的结果直接量化到设置的小数位宽上。
High radix时10/4=2.5的仿真

High radix时10/-4=-2.5的仿真
计算结果
整数部分fffd,为-3。
小数部分8000,没有符号位,为0.5
(计算结果加起来为-2.5,目前没有在pg151内找到相关说明)

High radix时10/-6=-1.666666的仿真
计算结果
整数部分fffe,为-2。
小数部分5555,没有符号位,为0.3333
(计算结果加起来为-1.6666)

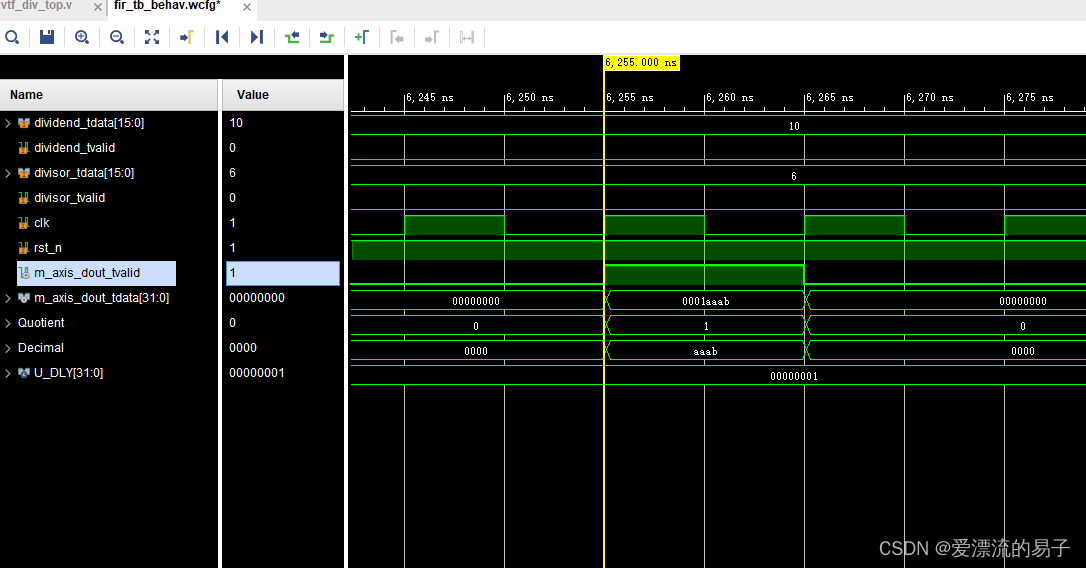
High radix时10/6=1.666666的仿真
计算结果
整数部分0001,为1。
小数部分aaab,没有符号位,为0.6666
(计算结果加起来为1.6666)