20240219画图程序

news2025/1/9 17:05:53

1. PTZ在惯性态时，不同视场角下的【发送】角速度和【理论响应】角速度

1.1 优化前

请添加图片描述

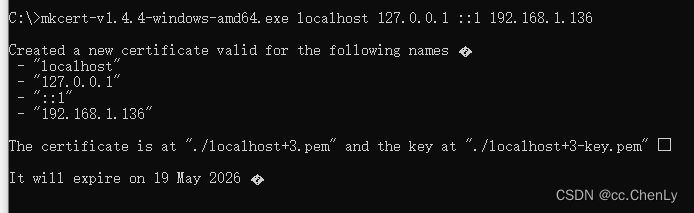
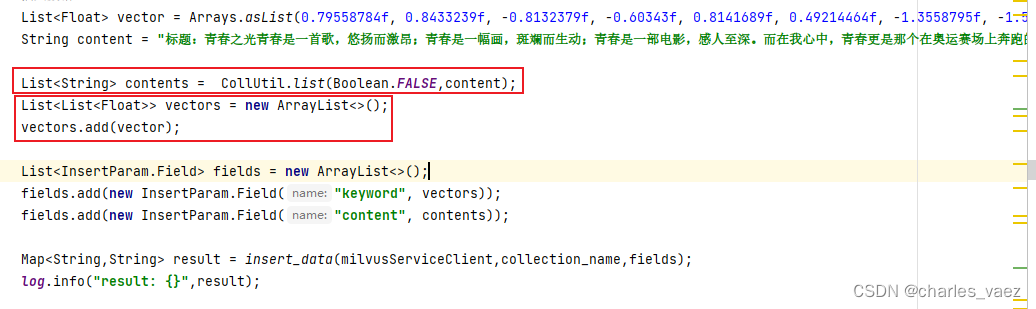
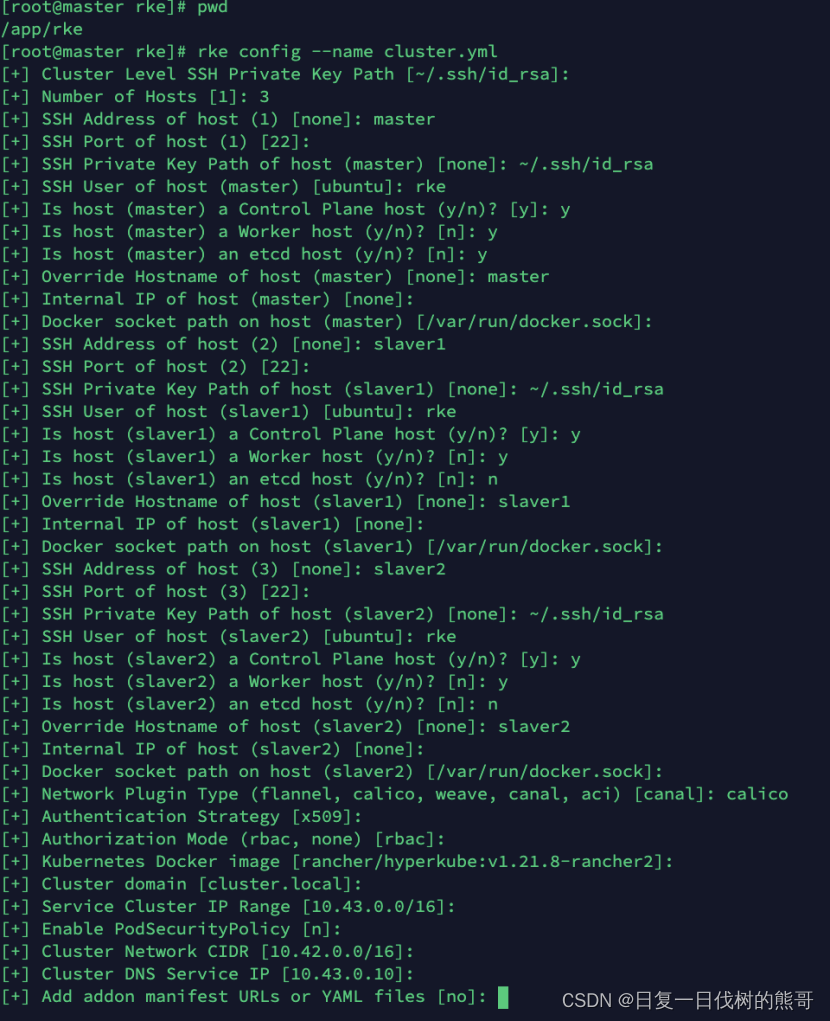
import numpy as np
import matplotlib.pyplot as plt

# PTZ在惯性态时，不同视场角下的【发送】角速度和【理论响应】角速度
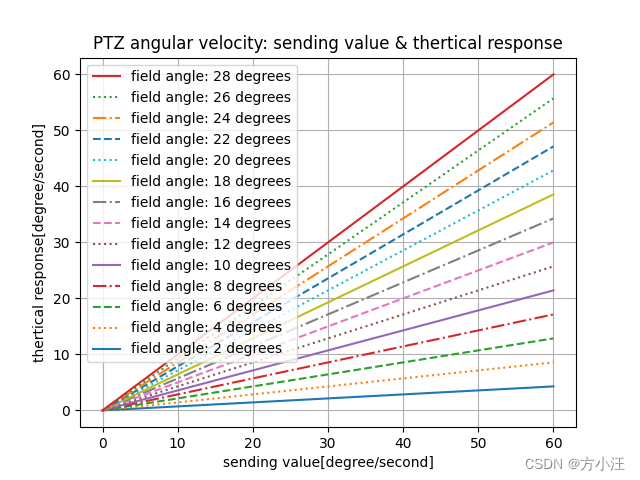
ATROffset_x = np.linspace(0, 60, 120)
y2 = ATROffset_x * 2 / 28
y4 = ATROffset_x * 4 / 28
y6 = ATROffset_x * 6 / 28
y8 = ATROffset_x * 8 / 28
y10 = ATROffset_x * 10 / 28
y12 = ATROffset_x * 12 / 28
y14 = ATROffset_x * 14 / 28
y16 = ATROffset_x * 16 / 28
y18 = ATROffset_x * 18 / 28
y20 = ATROffset_x * 20 / 28
y22 = ATROffset_x * 22 / 28
y24 = ATROffset_x * 24 / 28
y26 = ATROffset_x * 26 / 28
y28 = ATROffset_x * 28 / 28

plt.plot(ATROffset_x, y2, label='field angle: 2 degrees')
plt.plot(ATROffset_x, y4, linestyle='dotted',label='field angle: 4 degrees')
plt.plot(ATROffset_x, y6, linestyle='--',label='field angle: 6 degrees')
plt.plot(ATROffset_x, y8, linestyle='-.', label='field angle: 8 degrees')

plt.plot(ATROffset_x, y10, label='field angle: 10 degrees')
plt.plot(ATROffset_x, y12, linestyle='dotted', label='field angle: 12 degrees')
plt.plot(ATROffset_x, y14, linestyle='--',label='field angle: 14 degrees')
plt.plot(ATROffset_x, y16, linestyle='-.', label='field angle: 16 degrees')

plt.plot(ATROffset_x, y18, label='field angle: 18 degrees')
plt.plot(ATROffset_x, y20, linestyle='dotted', label='field angle: 20 degrees')
plt.plot(ATROffset_x, y22, linestyle='--',label='field angle: 22 degrees')
plt.plot(ATROffset_x, y24, linestyle='-.', label='field angle: 24 degrees')

plt.plot(ATROffset_x, y26, linestyle='dotted', label='field angle: 26 degrees')
plt.plot(ATROffset_x, y28, label='field angle: 28 degrees')

plt.xlabel('sending value[degree/second]')
plt.ylabel('thertical response[degree/second]')
plt.title('PTZ angular velocity: sending value & thertical response')
handles, labels = plt.gca().get_legend_handles_labels()
# plt.legend(handles[::-1], labels[::-1],loc='right')
plt.legend(handles[::-1], labels[::-1])
plt.grid()
plt.show()

1.2 优化后

请添加图片描述

import numpy as np
import matplotlib.pyplot as plt

ATROffset_x = np.linspace(0, 60, 120)
linestyles = ['-', 'dotted', '--', '-.', 
              '-', 'dotted', '--', '-.', 
              '-', 'dotted', '--', '-.', 
              '-', 'dotted']
labels = [f'field angle: {i} degrees' for i in range(2, 30, 2)]

for i, linestyle in enumerate(linestyles):
    y = ATROffset_x * (i + 2) / 28
    plt.plot(ATROffset_x, y, linestyle=linestyle, label=labels[i])

plt.xlabel('sending value[degree/second]')
plt.ylabel('thertical response[degree/second]')
plt.title('PTZ angular velocity: sending value & thertical response')
handles, labels = plt.gca().get_legend_handles_labels()
plt.legend(handles[::-1], labels[::-1])
plt.grid()
plt.show()

2. 像素偏移与发送角速度

请添加图片描述

import numpy as np
import matplotlib.pyplot as plt

# 分段函数
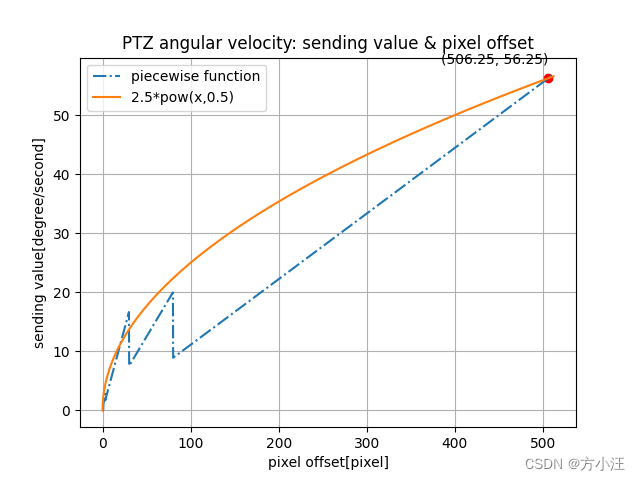
def piecewise_function(x):
    if x >80: return x/9
    elif x>30: return x/4
    elif x>10: return x/1.8
    elif x>3: return x/1.8
    elif x>1: return x
    else: return 0

# 生成x值
x = np.linspace(0, 512, 2000)
# 计算y值
y1 = [piecewise_function(xi) for xi in x]
y2 = 2.5*(x**(0.5))
# y3 = 2.5*(x**(0.8))

points = [(506.25, piecewise_function(506.25))]
for point in points:
    plt.plot(point[0], point[1], 'ro')
    plt.annotate(f'({point[0]}, {point[1]:.2f})', (point[0], point[1]), textcoords="offset points", xytext=(0,10), ha='center')

# 绘制图形
plt.plot(x, y1, label='piecewise function', linestyle='-.')
plt.plot(x, y2, label='2.5*pow(x,0.5)')
# plt.plot(x, y3, label='x**0.8')

plt.xlabel('pixel offset[pixel]')
plt.ylabel('sending value[degree/second]')
plt.title('PTZ angular velocity: sending value & pixel offset')
plt.grid()
plt.legend()
plt.show()

3. 估算不同焦距下的目标大小

3.1 原理

  • 【任务】：已知POD与目标之间的高度差3000m和水平距离2000m，需要解算7m*3m目标在POD观察画面中的大小
  • 【途径】：利用视场角解算视野大小，绘制目标在POD观察画面中的大小
    • 解算视场角大小：
      • fieldAngle_yaw = arctan(5.632/focalDistance)*180/Pi
      • fieldAngle_pitch = arctan(4.224/focalDistance)*180/Pi
    • 解算POD与目标的直线距离distance
    • 解算视野覆盖的实际长和宽
      • fieldWidth = 2*tan(fieldAngle_yaw/2)/disctance
      • fieldWidth = 2*tan(fieldAngle_pitch/2)/disctance
    • 解算目标在视野中的比例后，可得3.2中的图像

请添加图片描述

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 参数方程定义的单位球面
def sphere(u, v):
    theta = u * 2 * np.pi
    phi = v * np.pi
    x = np.sin(phi) * np.cos(theta)
    y = np.sin(phi) * np.sin(theta)
    z = np.cos(phi)
    return x, y, z

def plot_rectangle_tangent_to_point(point):
    # 计算点到原点的单位向量
    point_normalized = point / np.linalg.norm(point)

    # 找到一个与点到原点的向量垂直的向量
    perpendicular_vector_1 = np.cross(point_normalized, [1, 0, 0])
    if np.allclose(perpendicular_vector_1, [0, 0, 0]):
        # 如果点到原点的向量与[1, 0, 0]平行，则选择[0, 1, 0]作为第二个向量
        perpendicular_vector_1 = np.cross(point_normalized, [0, 1, 0])
    perpendicular_vector_1 /= np.linalg.norm(perpendicular_vector_1)

    # 找到与第一个向量垂直的第二个向量
    perpendicular_vector_2 = np.cross(point_normalized, perpendicular_vector_1)
    perpendicular_vector_2 /= np.linalg.norm(perpendicular_vector_2)

    # 生成矩形的四个顶点
    rectangle_half_side = 0.5  # 矩形边长的一半
    rectangle_vertices = np.array([
        point_normalized + rectangle_half_side * perpendicular_vector_1 + rectangle_half_side * perpendicular_vector_2,
        point_normalized - rectangle_half_side * perpendicular_vector_1 + rectangle_half_side * perpendicular_vector_2,
        point_normalized - rectangle_half_side * perpendicular_vector_1 - rectangle_half_side * perpendicular_vector_2,
        point_normalized + rectangle_half_side * perpendicular_vector_1 - rectangle_half_side * perpendicular_vector_2,
        point_normalized + rectangle_half_side * perpendicular_vector_1 + rectangle_half_side * perpendicular_vector_2  # 重复第一个点以闭合图形
    ])

    # 绘制矩形切面
    fig = plt.figure(figsize=(10, 10))
    ax = fig.add_subplot(111, projection='3d')
    ax.plot(rectangle_vertices[:, 0], rectangle_vertices[:, 1], rectangle_vertices[:, 2], color='r')
    ax.scatter(point[0], point[1], point[2], color='b', s=50)  # 绘制点

    # 定义两个点
    point1 = point
    point2 = np.array([0, 0, 0])
    # 绘制两个点
    ax.scatter(point1[0], point1[1], point1[2], color='r', s=100)
    ax.scatter(point2[0], point2[1], point2[2], color='b', s=100)
    # 绘制连线
    ax.plot([point1[0], point2[0]], [point1[1], point2[1]], [point1[2], point2[2]], color='k', linestyle='--')

    # 绘制中点
    fyo = (point_normalized + rectangle_half_side * perpendicular_vector_1 + rectangle_half_side * perpendicular_vector_2 + point_normalized + rectangle_half_side * perpendicular_vector_1 - rectangle_half_side * perpendicular_vector_2)/2
    ax.scatter(fyo[0], fyo[1], fyo[2], color='b', s=50)  # 绘制点
    # 绘制连线
    ax.plot([fyo[0], point2[0]], [fyo[1], point2[1]], [fyo[2], point2[2]], color='k', linestyle='--')
    # 绘制连线-平面内
    ax.plot([fyo[0], point[0]], [fyo[1], point[1]], [fyo[2], point[2]], color='k', linestyle='--')
      
    # 创建参数
    u = np.linspace(0, 2, 100)
    v = np.linspace(0, 2, 100)
    u, v = np.meshgrid(u, v)

    # 计算球面上的点
    x, y, z = sphere(u, v)

    # 绘制单位球面
    ax.plot_surface(x, y, z, color='b', alpha=0.02)
    # 画出xyz轴
    ax.plot([0, 1], [0, 0], [0, 0], color='red', linestyle='-', linewidth=2)
    ax.plot([0, 0], [0, 1], [0, 0], color='green', linestyle='-', linewidth=2)
    ax.plot([0, 0], [0, 0], [0, 1], color='blue', linestyle='-', linewidth=2)
    
    # 设置坐标轴等比例
    ax.set_box_aspect([1,1,1])

    # 设置坐标轴标签
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')

    # 设置x轴的刻度
    ax.set_xticks([-1, -0.5, 0, 0.5, 1])
    # 设置y轴的刻度
    ax.set_yticks([-1, -0.5, 0, 0.5, 1])
    # 设置z轴的刻度
    ax.set_zticks([-1, -0.5, 0, 0.5, 1])

    # 设置标题
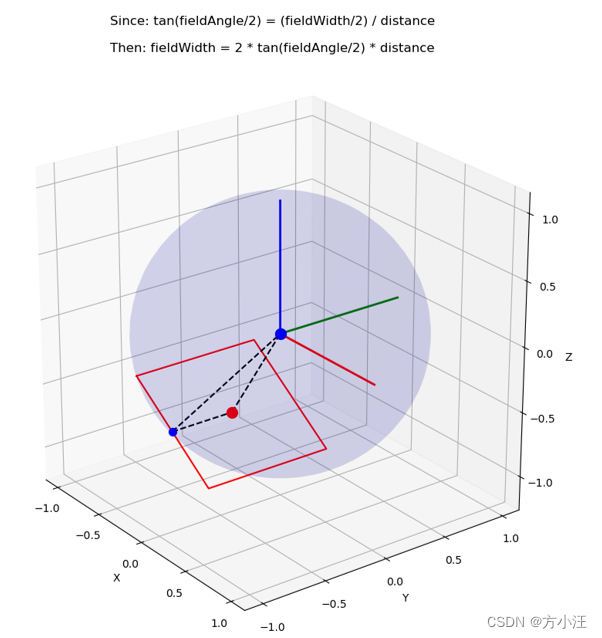
    plt.title("Since: tan(fieldAngle/2) = (fieldWidth/2) / distance\n\nThen: fieldWidth = 2 * tan(fieldAngle/2) * distance")

    plt.show()

point_on_sphere = np.array([-0.55, 0, -0.83])
plot_rectangle_tangent_to_point(point_on_sphere)

3.2 绘图

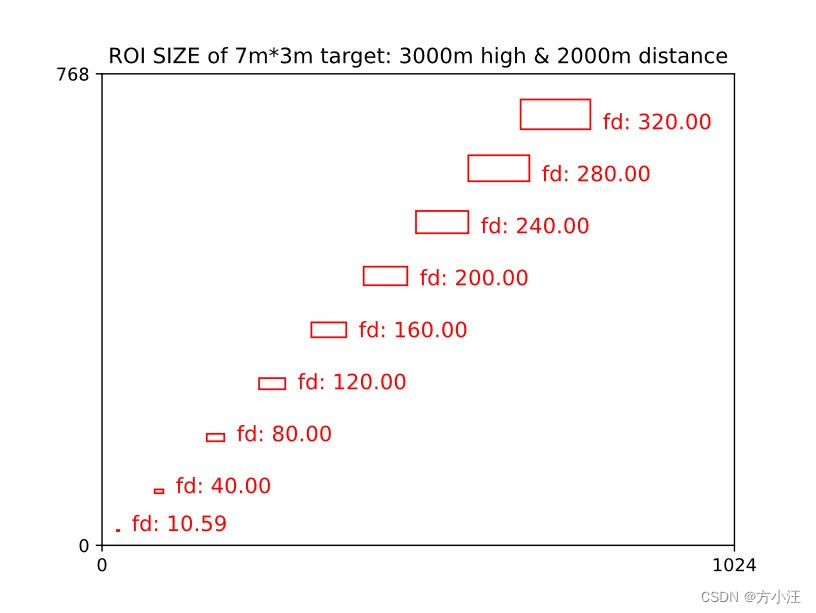
  • POD与目标之间高度差3000m、水平距离2000m，目标尺寸7m*3m
  • 不同焦距下，该目标在POD观察画面中的大小如图所示请添加图片描述
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import numpy as np
import math

relative_target_height = 3000
relative_target_horizontal = 2000
relative_distance = math.sqrt(relative_target_height*relative_target_height + relative_target_horizontal*relative_target_horizontal)
print("relative_distance: ", relative_distance)

fig, ax = plt.subplots()# 创建一个新的图形
plt.title("ROI SIZE of 7m*3m target: 3000m high & 2000m distance")# 设置标题

def fd2pic(fd):
    horizontal_draw = np.tan(math.atan(5.632/fd)/2) * relative_distance * 2
    vertical_draw = np.tan(math.atan(4.224/fd)/2) * relative_distance * 2
    # 添加第一个框
    rect = patches.Rectangle((6*7/horizontal_draw*1024, 14*3/vertical_draw*768), 
                             7/horizontal_draw*1024, 3/vertical_draw*768, linewidth=1, edgecolor='r', facecolor='none')
    ax.add_patch(rect)
    # 在第一个框旁边打印文字
    ax.text(7*7/horizontal_draw*1024+20, 14*3/vertical_draw*768, "fd: {:.2f}".format(fd), fontsize=12, color='r')

for i in range(9):
    fd2pic(max(40*i,10.59))

plt.xlim(0, 1024)
plt.ylim(0, 768)
plt.xticks([0, 1024])
plt.yticks([0, 768])
plt.show()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1457241.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

OpenAI 全新发布文生视频模型 Sora，支持 60s 超长长度，有哪些突破？将带来哪些影响？

OpenAI 全新发布文生视频模型 Sora，支持 60s 超长长度，有哪些突破？将带来哪些影响？

Sora大模型简介 OpenAI 的官方解释了在视频数据基础上进行大规模训练生成模型的方法。 我们下面会摘取其中的关键部分罗列让大家快速get重点。 喜欢钻研的伙伴可以到官网查看技术报告： https://openai.com/research/video-generation-models-as-world-simulator…
阅读更多...
【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目

【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目

C F 786 B − L e g a c y \mathrm{CF786B - Legacy} CF786B−Legacy D e s c r i p t i o n \mathrm{Description} Description 给定 1 1 1 张 n n n 个点的有向图，初始没有边，接下来有 q q q 次操作，形式如下： 1 u v w 表示…
阅读更多...
GO和KEGG富集分析

GO和KEGG富集分析

写在前面 我们《复现SCI文章系列教程》专栏现在是免费开放，推出这个专栏差不多半年的时间，但是由于个人的精力和时间有限，只更新了一部分。后续的更新太慢了。因此，最终考虑后还是免费开放吧，反正不是什么那么神秘的东…
阅读更多...
关于数据结构的定义以及基本的数据结构

关于数据结构的定义以及基本的数据结构

在计算机科学中，数据结构是指用于组织和存储数据的方式或方法。它涉及到在计算机内存中存储、管理和操作数据的技术和原则。数据结构不仅仅是简单地存储数据，还可以提供高效的数据访问和操作方式，以满足特定的需求。 以下是每个数据结构的详细…
阅读更多...
mkcert安装教程

mkcert安装教程

1、下载 官方文档：https://github.com/FiloSottile/mkcert#mkcert 下载链接：https://github.com/FiloSottile/mkcert/releases 2、安装，该文件目录下打开cmd（可以把文件复制到别的文件夹），执行命令 //命令…
阅读更多...
开源模型应用落地-工具使用篇-向量数据库进阶（四）

开源模型应用落地-工具使用篇-向量数据库进阶（四）

一、前言 通过学习"开源模型应用落地"系列文章，我们成功地建立了一个完整可实施的AI交付流程。现在，我们要引入向量数据库，作为我们AI服务的二级缓存。本文将继续基于上一篇“开源模型应用落地-工具使用篇-向量数据库（三…
阅读更多...
FreeRTOS移植到GD32

FreeRTOS移植到GD32

目录 一、GD32基础工程创建： 1、创建如下文件夹 2、在keil5创建工程 3、在工程添加相关.c文件和头文件路径 4、实例：实现LED闪烁功能 二、在基础工程添加FreeRTOS： 1、FreeRTOS中的文件: 2、添加的源文件: 3、添加的头文件路径: 4、…
阅读更多...
机器人常用传感器分类及一般性要求

机器人常用传感器分类及一般性要求

机器人传感器的分类 传感技术是先进机器人的三大要素（感知、决策和动作）之一。根据用途不同，机器人传感器可以分为两大类：用于检测机器人自身状态的内部传感器和用于检测机器人相关环境参数的外部传感器。 内部传感器 内部传感…
阅读更多...
【JavaEE】_HTML常用标签

【JavaEE】_HTML常用标签

目录 1.HTML结构 2. HTML常用标签 2.1 注释标签 2.2 标题标签：h1~h6 2.3 段落标签：p 2.4 换行标签：br 2.5 格式化标签 2.6 图片标签：img 2.7 超链接标签：a 2.8 表格标签 2.9 列表标签 2.10 表单标签 2.10…
阅读更多...
航班进出港|航班进出港管理系统|基于springboot航班进出港管理系统设计与实现(源码+数据库+文档)

航班进出港|航班进出港管理系统|基于springboot航班进出港管理系统设计与实现(源码+数据库+文档)

航班进出港管理系统目录 目录 基于springboot航班进出港管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 5、航班信息管理 （1） 航班信息管理 （2）起飞降落申请管理 （3）公告管理 &…
阅读更多...
辽宁博学优晨教育科技有限公司视频剪辑培训专业之选

辽宁博学优晨教育科技有限公司视频剪辑培训专业之选

随着数字时代的到来，视频剪辑技术已成为各行各业不可或缺的一项技能。为了满足市场需求，辽宁博学优晨教育科技有限公司（以下简称“博学优晨”）推出了专业的视频剪辑培训课程，旨在为广大学员提供系统、高效的学习机会。…
阅读更多...
AMD FPGA设计优化宝典笔记（4）复位桥

AMD FPGA设计优化宝典笔记（4）复位桥

高亚军老师的这本书《AMD FPGA设计优化宝典》，他主要讲了两个东西： 第一个东西是代码的良好风格； 第二个是设计收敛等的本质。 这个书的结构是一个总论，加上另外的9个优化，包含的有：时钟网络、组合逻辑、触…
阅读更多...
面试系列之《Spark》（持续更新...）

面试系列之《Spark》（持续更新...）

1.job&stage&task如何划分？ job：应用程序中每遇到一个action算子就会划分为一个job。 stage：一个job任务中从后往前划分，分区间每产生了shuffle也就是宽依赖则划分为一个stage，stage这体现了spark的pipeline思…
阅读更多...
picker选择器-年月日选择

picker选择器-年月日选择

从底部弹起的滚动选择器。支持五种选择器，通过mode来区分，分别是普通选择器，多列选择器，时间选择器，日期选择器，省市区选择器，默认是普通选择器。 学习一下日期选择器 平台差异说明 日期选择默…
阅读更多...
k8s学习（RKE+k8s+rancher2.x）成长系列之简配版环境搭建（三）

k8s学习（RKE+k8s+rancher2.x）成长系列之简配版环境搭建（三）

3.19.切换RKE用户，并做免密登录（三台机器相互免密） su rke cd~ ssh-keygen[rke@master.ssh]$ssh-copy-id rke@slaver2 [rke@master.ssh]$ssh-copy-id rke@slaver1 [rke@master.ssh]$ssh-copy-id rke@master3.20.搭建RKE集群 为了方便理解，我们把通RKE部署的Kubernetes集群称…
阅读更多...
浏览网页记录工具，企业如何查看员工网页浏览记录

浏览网页记录工具，企业如何查看员工网页浏览记录

随着信息技术的飞速发展，网络已成为企业日常运营和员工工作中不可或缺的一部分。然而，随之而来的是网络安全和员工上网行为管理的挑战。在这种情况下，浏览网页记录工具成为了企业监控员工上网行为的重要手段之一。 一、浏览网页记录工具的重要…
阅读更多...
MySQL 基础知识（十）之 MySQL 架构

MySQL 基础知识（十）之 MySQL 架构

目录 1 MySQL 架构说明 2 连接层 3 核心业务层 3.1 查询缓存 3.2 解析器 3.3 优化器 3.4 执行器 4 存储引擎层 5 参考文档 1 MySQL 架构说明 下图是 MySQL 5.7 及其之前版本的逻辑架构示意图 MySQL 架构大致可分为以下三层： 连接层：负责跟客户…
阅读更多...
unity学习（29）——GameInfo角色信息

unity学习（29）——GameInfo角色信息

1.把GameInfo.cs PlayerModel.cs Vector3.cs Vector4.cs PlayerStateConstans.cs GameState.cs依次粘到model文件夹中，此时项目没有错误，如下图所示； 对应处所修改的代码如下： case LoginProtocol.LOGIN_SRES://1 {Debug.Log(&qu…
阅读更多...
软件工程师，AI手机元年到来，我们怎么办

软件工程师，AI手机元年到来，我们怎么办

概述 OPPO创始人、总裁、CEO陈明永在2024年2月18日发表了名为《开启AI手机新时代》的内部信。陈明永认为：“2024年是AI手机元年。未来五年，AI对手机行业的影响，完全可以比肩当年智能手机替代功能机”。他预测AI手机时代将成为继功能机、智能手…
阅读更多...
docker jenkins 报错：script.sh.copy: 1: mvn: not found

docker jenkins 报错：script.sh.copy: 1: mvn: not found

找不到mvn,一般是没配置环境变量的问题。点开系统配置，设置环境变量即可
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023