KMP是什么
KMP是一种字符串匹配算法,能够判断字符串s2,是否为字符串s1的子串
例如:s1 = "abd123def",s2 = "123",KMP会返回4,代表s2是s1的子串,第一个匹配的下标为3
假设s1的数据规模为M,s2的数据规模为N
如果用暴力做法,由于对于s1中以每个字符开头,都有可能匹配出s2,因此最坏情况下有M次尝试,每次尝试耗时M,时间复杂度为O(M * N)
而KMP算法能做到查找的时间复杂度为O(M)
前缀和后缀串的最长匹配长度
首先定义一个概念:前缀以后缀串的最长匹配长度
为字符串中某个字符前面,不包括前面的整个字符串,相等的最长前缀和最长后缀的长度
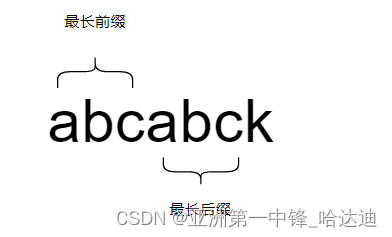
以字符串s = “abcabck"的最后一个字符k来说,最长且相等的前后缀为"abc”,长度为3
可以发现当前后缀为4,5时,前后缀不匹配,因此最长的匹配长度为3
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 前缀 | a | ab | abc | abca | abcab |
| 后缀 | c | bc | abc | cabc | bcabc |
| 是否相等 | 否 | 否 | 是 | 否 | 否 |
我们把s2(模式串)的每个字符都计算一次前缀以后缀串的最长匹配长度,得到next数组
对于"abcabck"来说,其next数组为:

其中第一个和第二个字符串的next值,人为规定为-1,0
为什么需要有这个next数组?因此可以让匹配过程加速
匹配
next数组可以在暴力匹配的过程中进行加速
回到一般的匹配情况,假设从s1的i位置,和s2的0位置开始匹配,直到s1的x位置,和s2的y位置发现不等
也就是说s1[i,x-1]和s2[0,y-1]是相等的
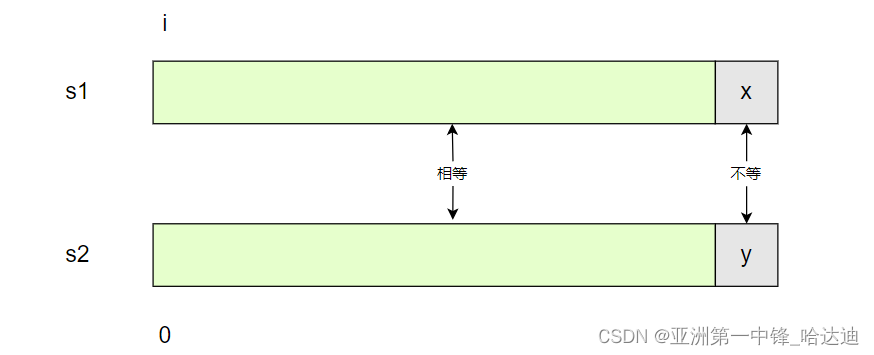
如果按照暴力匹配,需要将i往后移一个位置,从s1[i+1]和s2[0]开始匹配
但现在有字符串s2的next数组,可以对这个过程进行加速
当next值大于0
假设字符s2[y]有一个最长的前缀和后缀,分别为p1和p2,根据定义,p1等于p2
且s1[i,x-1] == s2[0,y-1],因此s1也有一个p1和p2,两者相等,而这4者是相等的:
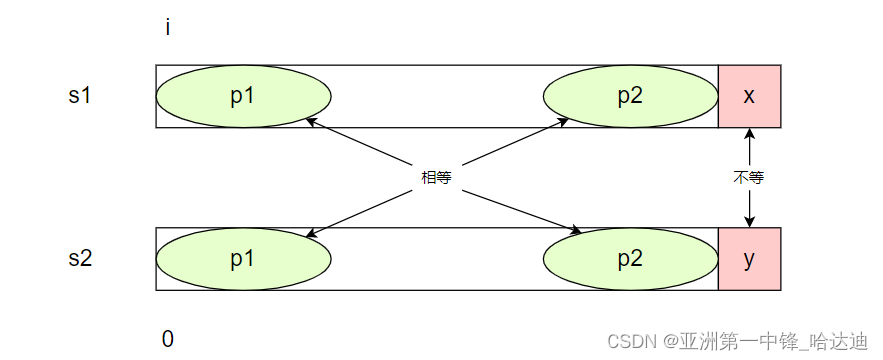
此时不用从s1[i+1]位置开始和s2[0]进行匹配,而是从s1中,p2的第一个位置j开始,和s2的0位置开始匹配:
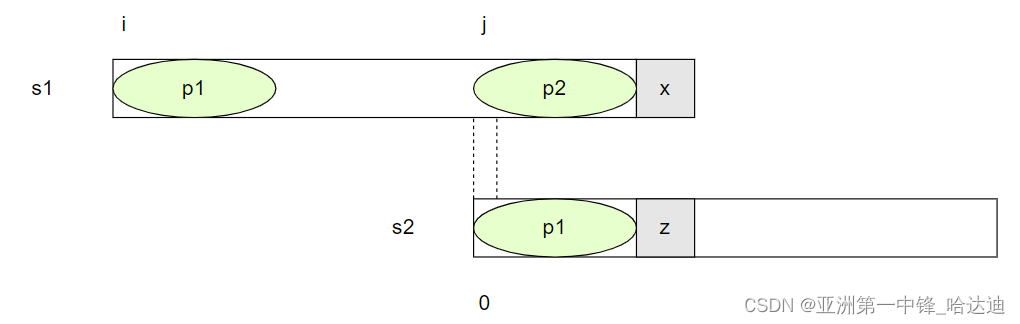
但由于s1的p2等于s2的p1,因此这一串不用比对,一定相等,直接从s1[x]和s2[z]位置开始匹配
这么做其实隐含了一个假设,s1从i+1位置,到j-1位置,都无法作为开头匹配出s2,所以才跳过这些位置,直接从j位置开始匹配
为什么这么假设成立呢?
我们假设s1能够从i+1位置,到j-1位置,可以作为开头匹配出s2,设该位置为k:
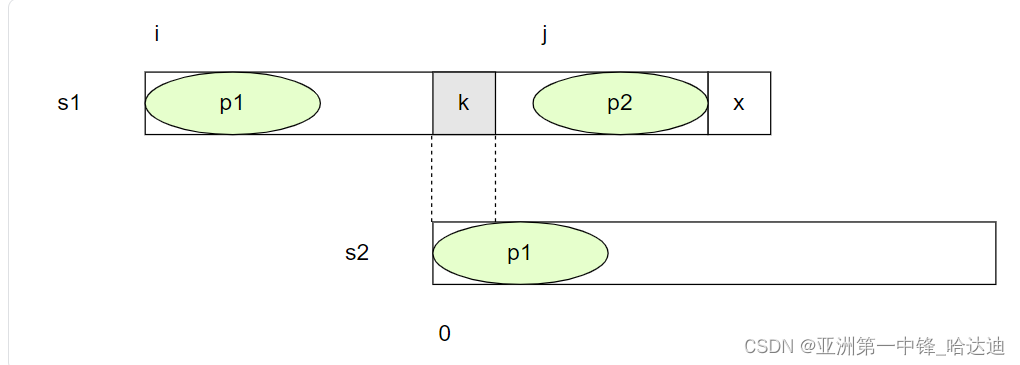
既然可以匹配出整个s2,那一定也可以匹配出从k到x-1这个长度的前缀:
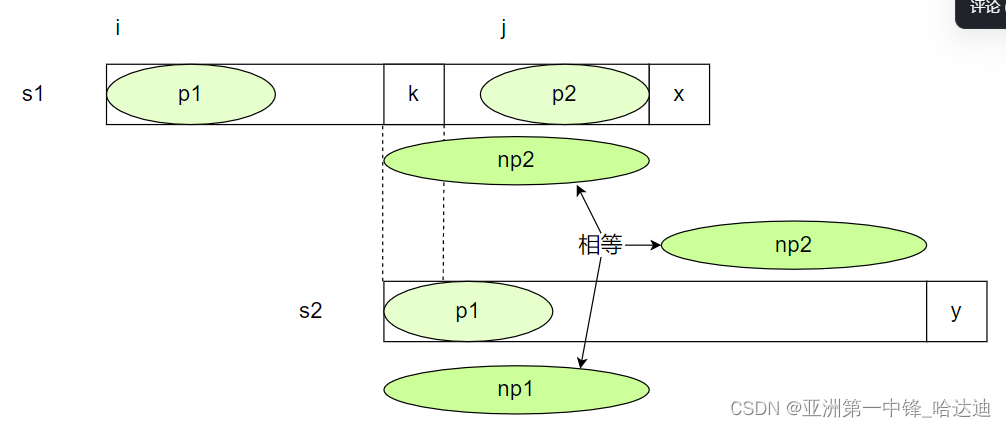
即上图中s1的np2等于s2的np1
而根据之前的匹配结果,s1的np2等于s2的np2
推出s2的np1等于s2的np2
这个结论和next数组中的信息矛盾了,
根据next[y]的信息,s2的最长匹配前后缀长度为p1的长度
但现在推出来s2[y]有更长的相等前缀后缀,因为np1比p1长,np2比p2长
因此假设假设s1能够从i+1位置,到j-1位置,可以作为开头匹配出s2不成立
这样就可以放心的放弃s1从i+1位置到j-1位置作为开头进行匹配的可能性
可以发现利用next数组的信息后,有两个加速点:
放弃s1从i+1位置到j-1位置作为开头进行匹配的可能性直接从s1[x]和s2[z]位置开始匹配
以上为next值大于0的情况,我们来看看当next值为0,-1时的做法:
当next值等于0
next值为0,即没有任何相等的前缀和后缀的匹配串,此时该如何进行下一步匹配呢?
此时从s1的x位置开始,和s2的0位置进行匹配
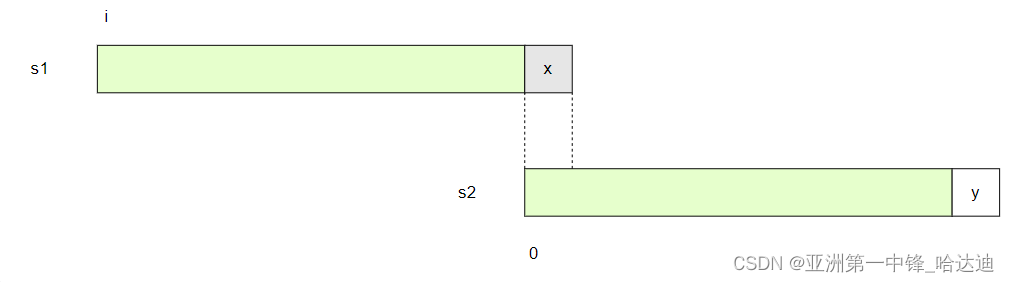
这里隐含了一个前提,即从s1的i位置开始,到x-1值,都无法匹配出完整的s2
还是用反证法证明,这个前提是成立的
假设不成立,即可以匹配出,假设从s1的k位置开始匹配,那一定有s1.p1等于s2.p1,而之前s1和s2是匹配到x,y才不相等的,因此s1.p2 等于s2.p2,推出s2.p1 等于 s2.p2
这和前提s2[y]的next值为0相矛盾了,因此假设不成立,前提成立,即从s1的i位置开始,到x-1值,都无法匹配出完整的s2
那只好从s1[x]开始匹配s2的[0]
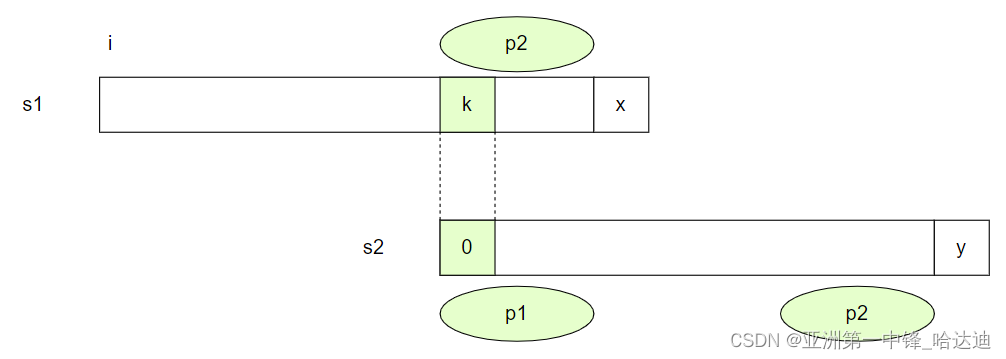
还有一种next值为0的情况,即人为规定第2个字符的next值为0
当s1[x]和s2[1]不等时,此时是从s1[x-1]和s2[0]开始,无法匹配出整个字符串
那么接下来就从s1[x]开始和s2[0]进行匹配就好了,这里和暴力解法一样,不跳过任何字符
当next值等于-1
next值为-1只有一种情况,就是认为规定的s2[0] = -1,当s1[x]和s2[0]不等时,从s1[x+1]开始和s2[0]进行匹配就好了
匹配代码
综合以上三种情况,可以写出如下的匹配代码:
public int indexOf(char[] s1, char[] s2) {
int x = 0;
int y = 0;
// 计算next数组,下文讲解
int[] next = getNext(s2);
while (x < s1.length && y < s2.length) {
// 匹配
if (s1[x] == s2[y]) {
x++;
y++;
continue;
}
// y == 0
if (next[y] == -1) {
x++;
continue;
}
// y跳到最长前后缀的下一个位置,即z开始和x进行比较
// 综合了next大于0和next等于0
y = next[y];
}
// 匹配成功
if (y == s2.length) {
return x - y;
}
// 匹配失败
return -1;
}
时间复杂度
要估计时间复杂度,需要估计while循环中的3个分支,这3个分支在每次while中只会中一个
定义两个量x,x-y,依次观察这3分支中,这两个量的变化情况

可以发现这两个量要么都推高,要么只推高一个,而这两个量上限都是O(M),因此时间复杂度为O(M)
计算next数组
我们从头到尾计算s2的next数组,假设当前计算到第i个位置
假设第i-1个位置的next值为a,对于s2[i-1]来说,有相等的前缀p1和p2
我们比较s2[i-1]和s2[a]是否相等,如果相等,则next[i]为a+1
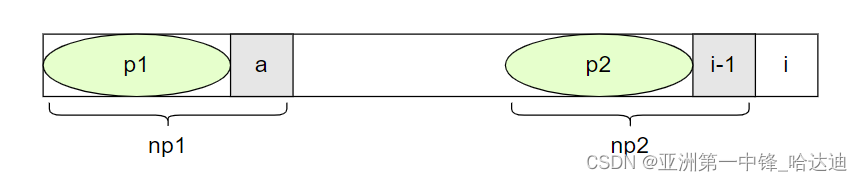
证明如下:
首先因为np1 = p1 + a,np2 = p2 + s[i-1],p1 == p2,s[a] == s[i-1],因此np1 == np2
此时对于s[i]来说,至少有长度为a+1的前缀和后缀相等
那有没有可能next[i]大于a+1呢?
假设有这个可能,设这两段多余的部分分别为n1,n2,如下图所示:
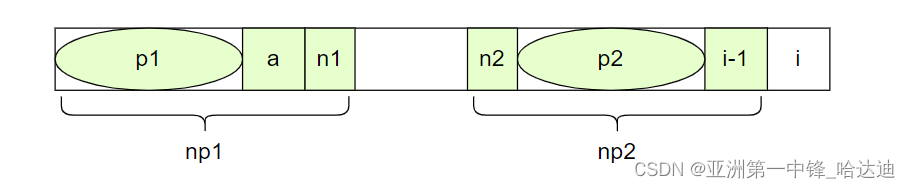
现在np1 = p1 + s2[a] + n1
np2 = n2 + p2 + s[i-1]
np1 == np2,既然这两个大串都相等了,那对于s[i-1]来说,这个大串的一部分n2 + p2 一定和一个等量的前缀相等,而这个前缀的长度超过了 next[i-1],和前提不符
因此next[i]不可能大于a+1,即s[i]就等于a+1
再来看当s2[i-1]和s2[a]不等的情况:

继续看s2[a]的最长前缀pp1下一个字符,和s2[i-1]是否相等,如果相等,next[i] = next[a] + 1
关于为什么排除掉next[a]+1,到a这个区间的可能性,同样可以用反证法证明
如果还不等,就继续往前看
代码如下:
private int[] getNext(char[] s2) {
if (s2.length == 1) {
return new int[]{-1};
}
int[] next = new int[s2.length];
next[0] = -1;
next[1] = 0;
// 目前在哪个位置求next
int i = 2;
// 需要和s2[i-1]比较的字符下标
int c = 0;
while (i < next.length) {
if (s2[i-1] == s2[c]) {
next[i] = c + 1;
i++;
c++;
// 如果s[i-1]和第一个字符不等,next[i] = 0
} else if (c == 0){
next[i] = 0;
i++;
} else {
c = next[c];
}
}
return next;
}