1.采用递归方式对顺序表进行快速排序,下列关于递归次数的叙述中,正确的是
A.每次划分后,先处理较长的分区可以减少递归次数
B.递归次数与初始数据的排列次序无关
C.每次划分后,先处理较短的分区可以减少递归次数
D.递归次数与每次划分后得到的分区处理顺序无关
答:D
析:
递归次数,取决于递归树,而递归树取决于轴枢的选择。树越平衡,递归次数越少。
而对分区的长短处理顺序,影响的是递归时对栈的使用内存,而不是递归次数。
A.递归次数与初始数据的排列次序有关,若有序,次数为O(N),理论上最少的次数为O(logN)。
B.C.每次划分后,先处理较短的分区,只是减少了递归占用的内存空间,并不能减少递归次数。
2.一棵完全二叉树第6层有9个叶节点(根为第1层),则节点个数最多有
A.111
B.112
C.107
D.109
答:D
析:
第6层有9个叶子节点,则可推测该二叉树最多有7层,节点总数为:
2^0 + 2^1 + 2^2 + 2^3 +2^4 +2^5 + 2*(32-9) = 109
3.对于序列16,14,10,8,7,9,3,2,4,1,以下说法正确的是
A.小顶推
B.大顶堆
C.不是堆
D.二叉排序树
答:B
析:

最大堆中所有父节点都比其左子树、右子树大。最小堆中所有的父节点都比其左子树、右子树小。
二叉排序树需要满足:左孩子<根<右孩子。
4.已知关键字序列5,8,12,19,28,20,15,22是最小堆,插入关键字3,调整后得到的最小堆是
A.3,8,12,5,20,15,22,28,19
B.3,5,12,19,20,15,22,8,28
C.3,12,5,8,28,20,15,22,19
D.3,5,12,8,28,20,15,22,19
答:D
析:
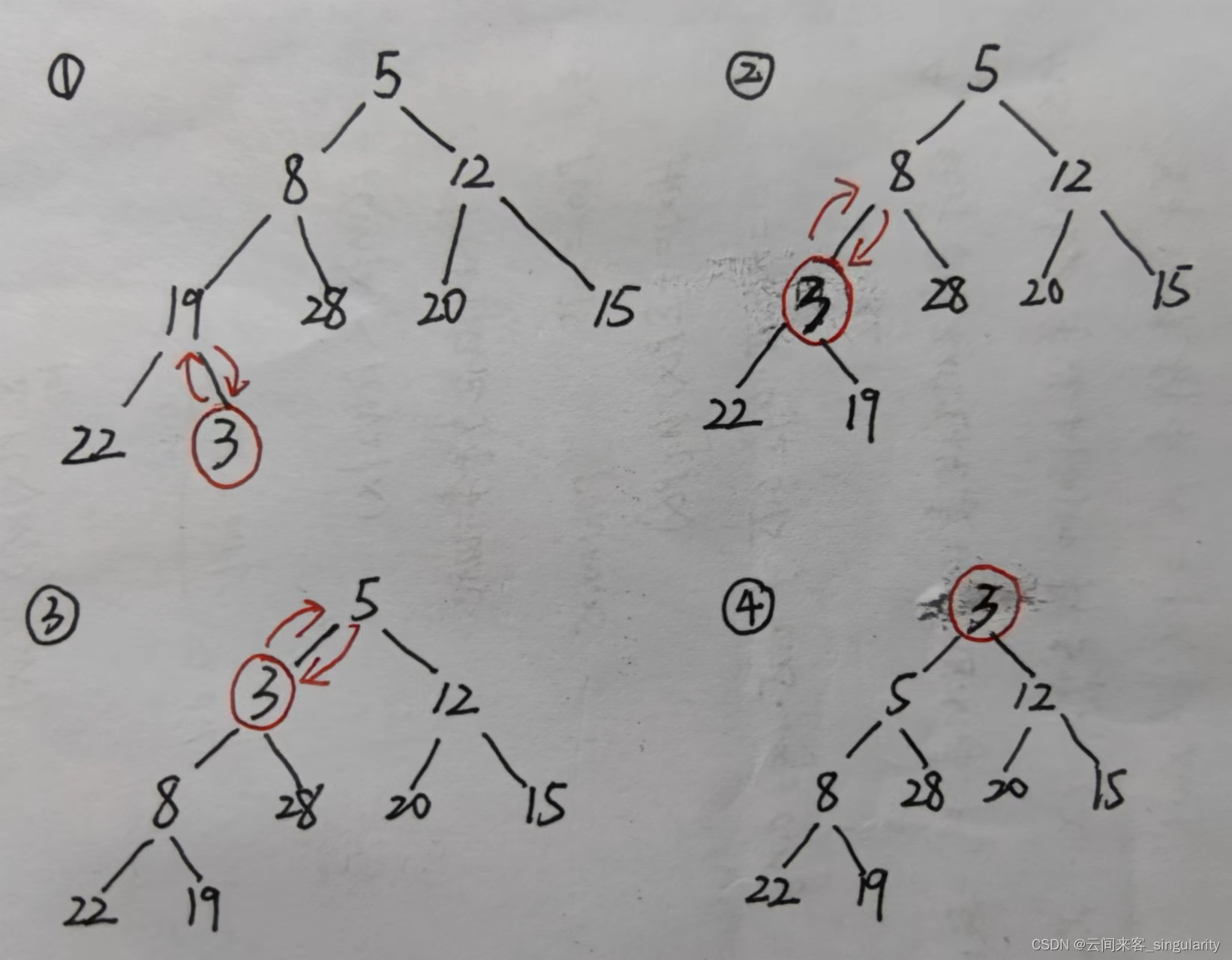
建堆,插入元素放在最后;将插入元素依次与父节点进行比较,若比父节点小,则与父节点替换进行堆调整,以此类推。
5.一棵二叉树的先序遍历为EFHIGJK,中序遍历为HFIEJKG,则后序遍历为
A.HIFJKGE
B.FHIJKGE
C.HIFGJKE
D.HIFKJGE
答:D
析:难点在右子树,多尝试。

6.对数组A[]={4,78,3,64,32,89,43,12}进行Hash存储时,选用H(K)=K%7作为Hash函数,则Hash地址为1的元素有几个
A.1
B.2
C.3
D.4
答:C
析:
H(k)=k%7;
H(78)=78%7=1
H(64)=64%7=1
H(43)=43%7=1
根据上述公式判断,这里只是问 Hash地址为1的元素,并没有涉及到实际存放的位置,而且冲突的处理方法也没有涉及,所以只要计算Hash后的值即可。
7.对于线性表(7,34,55,25,64,46,20,10)进行散列存储时,若使用H(K)=K%9作为散列函数,则散列地址为1的元素有几个
A.1
B.2
C.3
D.4
答:D
析:
55%9=1
64%9=1
46%9=1
10%9=1
8.已知一个线性表(38,25,74,63,52,48),假定采用散列函数h(key) = key%7 计算散列地址,并散列存储在散列表A[0....6]中,若采用线性探测方法解决冲突,则在该散列表上进行等概率成功查找的平均查找长度为
A.1.5
B.1.7
C.2.0
D.2.3
答:C
析:

平均查找长度 = 总的查找次数 / 元素数
总的查找次数: 38%7=3 (第1次出现3,无冲突,放在位置3,查找次数为1)
25%7=4(第1次出现4,无冲突,放在位置4,查找次数为1)
74%7=4(第2次出现4,有冲突,放在位置5,查找次数为2)
63%7=0(第1次出现0,无冲突,放在位置0,查找次数为1)
52%7=3(第2次出现3,有冲突,发现冲突3,4,5,故只能放到6,查找次数为4)
48%7=6 (第1次出现6,有冲突,发现冲突6,0,故只能放到1,查找次数为3)
1+1+2+1+4+3=12
元素数=6
所以:平均查找长度=12/6=2
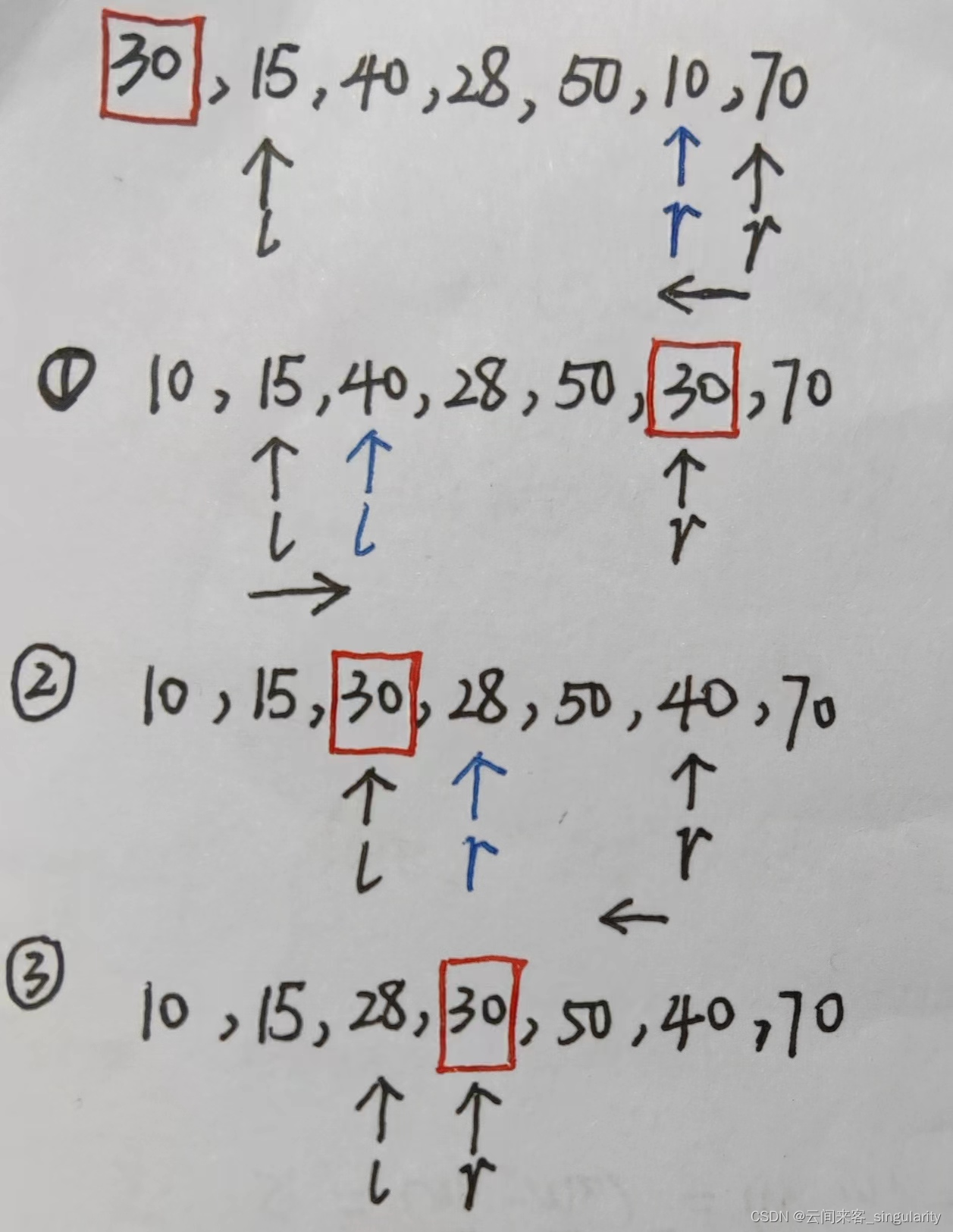
9.以30为基准,设一组初始记录关键字序列为 (30,15,40,28,50,10,70),则第一趟快速排序结果为
A 10,28,15,30,50,40,70
B 10,15,28,30,50,40,70
C 10,28,15,30,40,50,70
D 10,15,28,30,40,50,70
答:B
析:
初始化左指针为1,右指针为6
从右指针开始比较,右指针自减,到10的时候发现比30小,两者交换得到:10,15,40,28,50,30,70
从左指针开始比较,左指针自增,到40的时候发现比30大,两者交换得到:10,15,30,28,50,40,70
从右指针开始比较,右指针自减,到28的时候发现比30小,两者交换得到:10,15,28,30,50,40,70
此时完成第一趟排序,已经满足30的左边都比30小,右边都比30大
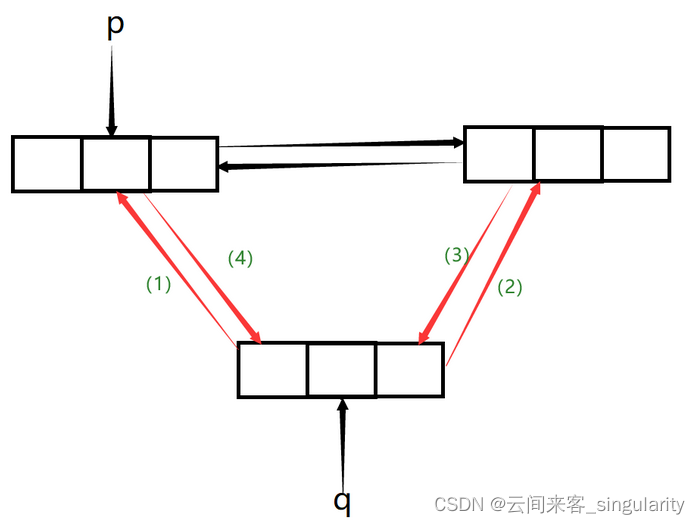
10.在双向循环链表中,在p指针所指的节点后插入一个指针q所指向的新节点,修改指针的操作是A.p->next=q;q->prior=p;p->next->prior=q;q->next=q;
B.p->next=q;p->next->prior=q;q->prior=p;q->next=p->next;
C.q->prior=p;q->next=p->next;p->next->prior=q;p->next=q;
D.q->next=p->next;q->prior=;p->next=q;p->next=q;
答:C
析:
- 双向链表插入首先将新加入的结点的两个指针指向正确位置即q->prior=p;q->next=p->next;
- 然后将原链表后面的那个结点前去指向新节点, p->next->prior=q;
- 将原链表前面的结点指向新节点 p->next=q;
最重要的顺序是:在q与原链表后面那个结点建立双向连接之前不可以改变p->next否则原链表断掉无法找到后面那个结点.