多元统计分析课程论文-聚类效果评价

news2024/11/28 10:38:37

数据集来源：Unsupervised Learning on Country Data (kaggle.com)

代码参考：Clustering: PCA| K-Means - DBSCAN - Hierarchical | | Kaggle

基于特征合成降维和主成分分析法降维的国家数据集聚类效果评价

目录

1.特征合成降维

2.PCA降维

3.K-Means聚类

3.1 对特征合成降维的数据聚类分析

3.2 对PCA降维的数据聚类分析

        摘要：本文主要探讨了特征合成降维和主成分分析法（PCA）降维在K-Means聚类中的效果评价。数据来源于HELP国际人道主义组织提供的168个国家的社会经济和健康领域的数据集，通过特征合成和PCA方法进行降维处理，再用K-Means聚类分析进行聚类，并使用轮廓系数对两种降维方法的数据集聚类效果进行评价。结果显示，特征合成降维的数据集的聚类效果优于PCA降维的数据集。尽管PCA降维保留了95.8%的原始信息，但其聚类效果较差，可能是由于数据失去原有结构等原因。

数据集变量及其解释

变量名

描述

country

国家名称

child_mort

每1000例活产婴儿中，5岁以下儿童死亡人数

exports

人均商品和服务出口。以占人均GDP的百分比给出

health

人均医疗总支出。以占人均GDP的百分比给出

imports

人均进口商品和服务。以占人均GDP的百分比给出

Income

人均净收入

Inflation

通货膨胀:衡量国内生产总值的年增长率

life_expec

寿命:按照目前的死亡率模式，新生儿的平均寿命

total_fer

按当前的年龄-生育率，每个妇女将生下的子女数量

gdpp

人均国内生产总值。以国内生产总值除以总人口计算

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
pd.options.display.float_format = '{:.2f}'.format
import warnings
warnings.filterwarnings('ignore')

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from mpl_toolkits.mplot3d import Axes3D

import plotly.express as px
import kaleido

data = pd.read_csv(r'F:\Jupyter Files\Practice\kaggle-聚类\Country-data.csv')
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
ut = np.triu(data.corr())
lt = np.tril(data.corr())
colors = ['#FF781F','#2D2926']
fig,ax = plt.subplots(nrows = 1, ncols = 2,figsize = (15,5))
plt.subplot(1,2,1)
sns.heatmap(data.corr(),cmap = colors,annot = True,cbar = 'True',mask = ut);
plt.title('相关系数矩阵:上三角格式');

plt.subplot(1,2,2)
sns.heatmap(data.corr(),cmap = colors,annot = True,cbar = 'True',mask = lt);
plt.title('相关矩阵:下三角格式');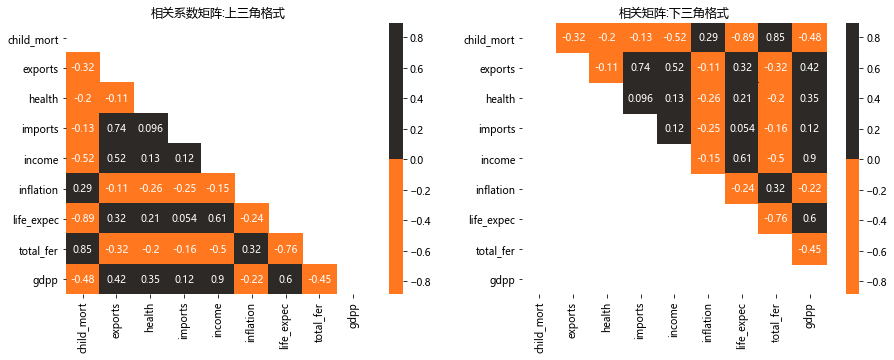

1.特征合成降维

变量合成规则表

类别

合并变量

健康类

child_mort,Health, life_expecc, total_fer

贸易类

exports, imports

金融类

Income, Inflation, gdpp

df1 = pd.DataFrame()
df1['健康类'] = (data['child_mort'] / data['child_mort'].mean()) + (data['health'] / data['health'].mean()) +(data['life_expec'] / data['life_expec'].mean()) + (data['total_fer'] / data['total_fer'].mean())
df1['贸易类'] = (data['imports'] / data['imports'].mean()) + (data['exports'] / data['exports'].mean())
df1['经济类'] = (data['income'] / data['income'].mean()) + (data['inflation'] / data['inflation'].mean()) + (data['gdpp'] / data['gdpp'].mean())
fig,ax = plt.subplots(nrows = 1,ncols = 1,figsize = (5,5))
plt.subplot(1,1,1)
sns.heatmap(df1.describe().T[['mean']],cmap = 'Oranges',annot = True,fmt = '.2f',linecolor = 'black',linewidths = 0.4,cbar = False);
plt.title('Mean Values');
fig.tight_layout(pad = 4)

col = list(df1.columns)
numerical_features = [*col]
fig, ax = plt.subplots(nrows = 1,ncols = 3,figsize = (12,4))
for i in range(len(numerical_features)):
    plt.subplot(1,3,i+1)
    sns.distplot(df1[numerical_features[i]],color = colors[0])
    title = '变量 : ' + numerical_features[i]
    plt.title(title)
plt.show()

#归一化处理
from sklearn.preprocessing import MinMaxScaler,StandardScaler
mms = MinMaxScaler() # Normalization
ss = StandardScaler() # Standardization
df1['健康类'] = mms.fit_transform(df1[['健康类']])
df1['贸易类'] = mms.fit_transform(df1[['贸易类']])
df1['经济类'] = mms.fit_transform(df1[['经济类']])
df1.insert(loc = 0, value = list(data['country']), column = 'Country')
df1.head()
Country健康类贸易类经济类
0Afghanistan0.630.140.08
1Albania0.130.200.09
2Algeria0.180.190.21
3Angola0.660.280.24
4Antigua and Barbuda0.120.280.15

2.PCA降维

col = list(data.columns)
col.remove('country')
categorical_features = ['country']
numerical_features = [*col]
print('Categorical Features :',*categorical_features)#分类型变量
print('Numerical Features :',*numerical_features)#数据型变量
Categorical Features : country
Numerical Features : child_mort exports health imports income inflation life_expec total_fer gdpp
fig, ax = plt.subplots(nrows = 3,ncols = 3,figsize = (15,15))
for i in range(len(numerical_features)):
    plt.subplot(3,3,i+1)
    sns.distplot(data[numerical_features[i]],color = colors[0])
    title =  numerical_features[i]
plt.show()

#对health变量做标准化处理，对其余变量进行归一化处理
df2 = data.copy(deep = True)
col = list(data.columns)
col.remove('health'); col.remove('country')
df2['health'] = ss.fit_transform(df2[['health']]) # Standardization
for i in col:
    df2[i] = mms.fit_transform(df2[[i]]) # Normalization
df2.drop(columns = 'country',inplace = True)

利用 SPSS 软件对处理后的数据进行检验，由表3得，KMO值为 0.678(>0.5)，达到主成分分析的标准，且 Bartlett检验显著性水平值为 0.000 小于 0.05，说明样本数据适宜做主成分分析。

from sklearn.decomposition import PCA
pca = PCA()
pca_df2 = pd.DataFrame(pca.fit_transform(df2))
pca.explained_variance_
array([1.01740511, 0.13090418, 0.03450018, 0.02679822, 0.00979752,
       0.00803398, 0.00307055, 0.00239976, 0.00179388])
fig,ax = plt.subplots(nrows = 1,ncols = 1,figsize = (10,5),dpi=80)
plt.step(list(range(1,10)), np.cumsum(pca.explained_variance_ratio_))
# plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('主成分个数')
plt.ylabel('主成分累计贡献率')
plt.show()

3.K-Means聚类

m1 = df1.drop(columns = ['Country']).values # Feature Combination : Health - Trade - Finance
m2 = pca_df2.values # PCA Data
3.1 对特征合成降维的数据聚类分析
sse = {};sil = [];kmax = 10
fig = plt.subplots(nrows = 1, ncols = 2, figsize = (20,5))

# Elbow Method 肘部法则:
plt.subplot(1,2,1)
for k in range(1, 10):
    kmeans = KMeans(n_clusters=k, max_iter=1000).fit(m1)
    sse[k] = kmeans.inertia_ # Inertia: Sum of distances of samples to their closest cluster center
sns.lineplot(x = list(sse.keys()), y = list(sse.values()));
plt.title('Elbow Method')
plt.xlabel("k : Number of cluster")
plt.ylabel("Sum of Squared Error")
plt.grid()

# Silhouette Score Method
plt.subplot(1,2,2)
for k in range(2, kmax + 1):
    kmeans = KMeans(n_clusters = k).fit(m1)
    labels = kmeans.labels_
    sil.append(silhouette_score(m1, labels, metric = 'euclidean'))
sns.lineplot(x = range(2,kmax + 1), y = sil);
plt.title('Silhouette Score Method')
plt.xlabel("k : Number of cluster")
plt.ylabel("Silhouette Score")
plt.grid()

plt.show()

model = KMeans(n_clusters = 3,max_iter = 1000,algorithm="elkan")
model.fit(m1)
cluster = model.cluster_centers_
centroids = np.array(cluster)
labels = model.labels_
data['Class'] = labels; df1['Class'] = labels

fig = plt.figure(dpi=100)
ax = Axes3D(fig)
x = np.array(df1['健康类'])
y = np.array(df1['贸易类'])
z = np.array(df1['经济类'])
ax.scatter(centroids[:,0],centroids[:,1],centroids[:,2],marker="X", color = 'b')
ax.scatter(x,y,z,c = y)
plt.title('健康类-贸易类-经济类数据聚类结果可视化')
ax.set_xlabel('健康类')
ax.set_ylabel('贸易类')
ax.set_zlabel('经济类')
plt.show();

fig, ax = plt.subplots(nrows = 1, ncols = 2, figsize = (15,5))
plt.subplot(1,2,1)
sns.boxplot(x = 'Class', y = 'child_mort', data  = data, color = '#FF781F');
plt.title('child_mort vs Class')
plt.subplot(1,2,2)
sns.boxplot(x = 'Class', y = 'income', data  = data, color = '#FF781F');
plt.title('income vs Class')
plt.show()

df1['Class'].loc[df1['Class'] == 0] =  'Might Need Help'
df1['Class'].loc[df1['Class'] == 1] ='No Help Needed'
df1['Class'].loc[df1['Class'] == 2] = 'Help Needed'

fig = px.choropleth(df1[['Country','Class']],
                    locationmode = 'country names',
                    locations = 'Country',
                    title = 'Needed Help Per Country (World)',
                    color = df1['Class'],  
                    color_discrete_map = {'Help Needed':'Red',
                                        'No Help Needed':'Green',
                                        'Might Need Help':'Yellow'}
                   )
fig.update_geos(fitbounds = "locations", visible = True)
fig.update_layout(legend_title_text = 'Labels',legend_title_side = 'top',title_pad_l = 260,title_y = 0.86)
fig.show(engine = 'kaleido')

3.2 对PCA降维的数据聚类分析
sse = {};sil = [];kmax = 10
fig = plt.subplots(nrows = 1, ncols = 2, figsize = (20,5))

# Elbow Method 肘部法则 :
plt.subplot(1,2,1)
for k in range(1, 10):
    kmeans = KMeans(n_clusters=k, max_iter=1000).fit(m2)
    sse[k] = kmeans.inertia_ # Inertia: Sum of distances of samples to their closest cluster center
sns.lineplot(x = list(sse.keys()), y = list(sse.values()));
plt.title('Elbow Method')
plt.xlabel("k : Number of cluster")
plt.ylabel("Sum of Squared Error")
plt.grid()

# Silhouette Score Method
plt.subplot(1,2,2)
for k in range(2, kmax + 1):
    kmeans = KMeans(n_clusters = k).fit(m2)
    labels = kmeans.labels_
    sil.append(silhouette_score(m2, labels, metric = 'euclidean'))
sns.lineplot(x = range(2,kmax + 1), y = sil);
plt.title('Silhouette Score Method')
plt.xlabel("k : Number of cluster")
plt.ylabel("Silhouette Score")
plt.grid()

plt.show()


model = KMeans(n_clusters = 3,max_iter = 1000,algorithm="elkan")
model.fit(m2)
cluster = model.cluster_centers_
centroids = np.array(cluster)
labels = model.labels_
data['Class'] = labels; pca_df2['Class'] = labels

fig = plt.figure(dpi=100)
ax = Axes3D(fig)
ax.scatter(centroids[:,0],centroids[:,1],centroids[:,2],marker="X", color = 'b')
plt.title('PCA降维数据聚类结果可视化')
ax.set_xlabel('第一主成分')
ax.set_ylabel('第二主成分')
ax.set_zlabel('第三主成分')
ax.scatter(x,y,z,c = y)
plt.show();

fig, ax = plt.subplots(nrows = 1, ncols = 2, figsize = (15,5))
plt.subplot(1,2,1)
sns.boxplot(x = 'Class', y = 'child_mort', data  = data, color = '#FF781F');
plt.title('child_mort vs Class')
plt.subplot(1,2,2)
sns.boxplot(x = 'Class', y = 'income', data  = data, color = '#FF781F');
plt.title('income vs Class')
plt.show()

pca_df2['Class'].loc[pca_df2['Class'] == 0] = 'Might Need Help'
pca_df2['Class'].loc[pca_df2['Class'] == 1] = 'No Help Needed'
pca_df2['Class'].loc[pca_df2['Class'] == 2] = 'Help Needed' 

fig = px.choropleth(pca_df2[['Country','Class']],
                    locationmode = 'country names',
                    locations = 'Country',
                    title = 'Needed Help Per Country (World)',
                    color = pca_df2['Class'],  
                    color_discrete_map = {'Help Needed':'Red',
                                          'Might Need Help':'Yellow',
                                          'No Help Needed': 'Green'})
fig.update_geos(fitbounds = "locations", visible = True)
fig.update_layout(legend_title_text = 'Labels',legend_title_side = 'top',title_pad_l = 260,title_y = 0.86)
fig.show(engine = 'kaleido')

3.3 轮廓系数效果评价

        轮廓系数是一种用于评估聚类效果的指标。它是对每个样本来定义的，它能够同时衡量样本与其自身所在的簇中的其他样本的相似度a和样本与其他簇中的样本的相似度b，其中，a等于样本与同一簇中所有其他点之间的平均距离；b等于样本与下一个最近的簇中得所有点之间的平均距离。单个样本的轮廓系数计算为：

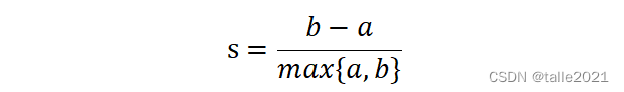
根据聚类的要求“簇内差异小，簇外差异大”，当轮廓系数越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似。如果一个簇中的大多数样本具有比较高的轮廓系数，则簇会有较高的总轮廓系数，即整个数据集的平均轮廓系数越高，则聚类效果是合适的。

#特征合成降维的数据集
cluster_1=KMeans(n_clusters=3,random_state=0).fit(m1)
silhouette_score(m1,cluster_1.labels_) #0.452
#PCA降维的数据集
cluster_2=KMeans(n_clusters=3,random_state=0).fit(m2)
silhouette_score(m2,cluster_2.labels_) #0.384
两种降维方法数据的轮廓系数

特征合成降维的数据集

PCA降维的数据集

轮廓系数

0.452

0.384

ps：低价出课程论文-多元统计分析论文、R语言论文、stata计量经济学课程论文（论文+源代码+数据集）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1456131.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Redis哨兵模式的搭建

Redis哨兵模式的搭建

文章目录 1、原理2、准备2.1、服务器准备2.2、资源准备 3、Redis 主从搭建3.1、Redis 安装3.2、redis.conf 配置3.2.1、Redis 主配置3.2.2、Redis 从配置 3.3、Redis 启动3.4、Redis 状态3.4.1、master 节点信息3.4.2、slave节点信息 4、哨兵配置4.1、sentinel.conf配置4.2、re…
阅读更多...
ChatGPT-用ChatGPT指令，自学任何领域的系统知识

ChatGPT-用ChatGPT指令，自学任何领域的系统知识

1. 指令位置 Github仓库：Mr Ranedeer AI Tutor 但是需要开通chatgtp plus版本，并且打开代码解释器 2 使用 学习内容 开始学习 AI甚至可以给你思考题，给出的答案还能进行评价 配置 通过配置表修改 深度 学习风格 沟通风格 语气风格 推…
阅读更多...
1Panel使用GMSSL+Openresty实现国密/RSA单向自适应

1Panel使用GMSSL+Openresty实现国密/RSA单向自适应

本文 首发于 Anyeの小站，转载请取得作者同意。 前言 国密算法是国家商用密码算法的简称。自2012年以来，国家密码管理局以《中华人民共和国密码行业标准》的方式，陆续公布了SM2/SM3/SM4等密码算法标准及其应用规范。其中“SM”代表“商密”&a…
阅读更多...
iOS如何一键清除剪贴板中的所有内容

iOS如何一键清除剪贴板中的所有内容

参考:https://www.jb51.net/shouji/746688.html 1.打开“快捷指令”应用，前往“快捷指令中心”，下拉找到“巧用剪贴板”并点击“查看全部”。 2.下拉到底部，点击“清除剪贴板中的所有内容”，然后选择“添加快捷指令”&#xff1a…
阅读更多...
sdxl-turbo、playground文生图模型使用案例

sdxl-turbo、playground文生图模型使用案例

1、sdxl-turbo SDXL-Turbo是一种快速生成的文本到图像模型，可以在单个网络评估中从文本提示合成逼真的图像。 参考：https://huggingface.co/stabilityai/sdxl-turbo 对比效果相比PixArt模型差很多，参考https://blog.csdn.net/weixin_42357472/article/details/135520142 …
阅读更多...
MySQL数据库基础（八）：DML数据操作语言

MySQL数据库基础（八）：DML数据操作语言

文章目录 DML数据操作语言 一、DML包括哪些SQL语句 二、数据的增删改（重点） 1、数据的增加操作 2、数据的修改操作 3、数据的删除操作 DML数据操作语言 一、DML包括哪些SQL语句 insert插入、update更新、delete删除 二、数据的增删改&#xff08…
阅读更多...
05.QT坐标系

05.QT坐标系

1. 坐标系原点 坐标系原点就是屏幕/窗口的左上角，X向右增长，Y向下增长。 2.设置控件位置 设置控件位置，就相当于是需要指定控件的坐标，对于该控件来说，其坐标原点是其父窗口/父控件的左上角。 设置方法就是通过控件的…
阅读更多...
认识ansible，了解常用的模块

认识ansible，了解常用的模块

ansible的概念 Ansible是一个基于Python开发的配置管理和应用部署工具，现在也在自动化管理领域大放异彩。它融合了众多老牌运维工具的优点，Pubbet和Saltstack能实现的功能，Ansible基本上都可以实现。 Ansible能批量配置、部署、管理上千台主…
阅读更多...
VS code常用插件

VS code常用插件

1.Auto Close Tag （自动闭合HTML/XML标签） 2.Auto Rename Tag （自动完成另一侧标签的同步修改） Beautify （格式化 html ,js,css） 4.Bracket Pair Colorizer（将匹配的括号染成相同的颜色&#xf…
阅读更多...
利用 pt-archiver 实现数据库归档功能

利用 pt-archiver 实现数据库归档功能

文章目录 一、前言关于Percona 二、Percona Toolkit安装 percona-toolkit：pt-archiver 归档命令的使用格式：示例： 三、归档步骤：1）、创建归档数据库和归档表方式一(推荐)：这种方式的优缺点： 方式…
阅读更多...
【软考问题】-- 13 - 知识精讲 - 项目绩效域管理

【软考问题】-- 13 - 知识精讲 - 项目绩效域管理

一、基本问题 问题1：干系人绩效域的预期目标主要包含什么？ ①与干系人建立高效的工作关系；②干系人认同项目目标；③支持项目的干系人提高了满意度，并从中收益；④反对项目的干系人没有对项目产生负面影响。问…
阅读更多...
黑莓加大裁员力度，目标年利润再增1亿美元

黑莓加大裁员力度，目标年利润再增1亿美元

近日，加拿大黑莓公司表示，今年的年利润再度增加 1 亿美元，为此将采取包括裁员在内的一系列降本措施。黑莓方面称，公司将在本季度进一步降低成本，并在网络安全业务上进行额外裁员，从而每年为公司节省约 2700…
阅读更多...
MyBatis终版

MyBatis终版

MyBatis常见面试题汇总（超详细回答） 1.什么是Mybatis？ Mybatis是一种流行的Java对象关系映射（ORM）框架，它将Java对象映射到关系型数据库中的表格。它提供了一种简单的方式来编写SQL语句并将其映射到Java对…
阅读更多...
加了AI的旗舰版，会用就是好工具！

加了AI的旗舰版，会用就是好工具！

软件简介： 软件【下载地址】获取方式见文末。注：推荐使用，更贴合此安装方法！ ACDSee Photo Studio Ultimate 2024是一款功能强大的数字图像预览和编辑软件，适用于专业的图像处理需求。它配备了高效的RAW编辑器&#…
阅读更多...
C++并发编程 -3.同步并发操作

C++并发编程 -3.同步并发操作

本文介绍如何使用条件变量控制并发的同步操作、C 并发三剑客，函数式编程 一.条件变量 1.概念 C条件变量（condition variable）是一种多线程编程中常用的同步机制，用于线程间的通信和协调。它允许一个或多个线程等待某个条件的发生…
阅读更多...
数据脱敏(四)脱敏算法-替换算法

数据脱敏(四)脱敏算法-替换算法

脱敏算法篇使用阿里云数据脱敏算法为模板,使用算子平台快速搭建流程来展示数据 "替换脱敏"是一种数据处理技术，主要用于保护个人隐私和数据安全。它通过将敏感信息（如姓名、身份证号、电话号码等）替换为无意义或随机的字符&#xf…
阅读更多...
hal/SurfaceFlinger/perfetto实战需求问题探讨作业-千里马framework开发

hal/SurfaceFlinger/perfetto实战需求问题探讨作业-千里马framework开发

背景 hi，粉丝朋友们： 在新课halperfettosurfaceflinger https://mp.weixin.qq.com/s/LbVLnu1udqExHVKxd74ILg 推出后，各位学员朋友们都积极响应，开始马不停蹄的学习，学员学习后希望有更多的实战案例或者项目拿来练手&…
阅读更多...
vue3中基于路由层面和组件层面进行用户角色及权限控制的方法解析

vue3中基于路由层面和组件层面进行用户角色及权限控制的方法解析

文章目录 一、权限控制二、路由层面控制三、组件层面控制1、使用自定义指令2、使用方法控制3、封装一个权限控制组件来实现组件层面控制权限3.1、组件页面 Authority.vue3.2、使用页面 app.vue3.3、效果预览 一、权限控制 随着前端技术的不断发展，越来越多的前端框…
阅读更多...
美食推荐|美食推荐小程序|基于微信小程序的美食推荐系统设计与实现(源码+数据库+文档)

美食推荐|美食推荐小程序|基于微信小程序的美食推荐系统设计与实现(源码+数据库+文档)

美食推荐小程序目录 目录 基于微信小程序的美食推荐系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、前台功能模块 2、后台功能模块 （1）用户信息管理 （2）水果信息管理 （3）水果类型管理…
阅读更多...
投票助力 | 第19届（2023）数智招标采购行业年度评选网络投票已开启！

投票助力 | 第19届（2023）数智招标采购行业年度评选网络投票已开启！

为展示招标采购领域业务发展的突出成绩和数智化应用创新成果，以优秀企业、个人和案例激励并引导更多的行业实践者们共同努力，推进招标采购行业数智化创新发展，必联网、机电产品招标投标电子交易平台、隆道平台、隆道研究院联合主办了“第19届…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023