目录
面试题 49 : 从根节点到叶节点的路径数字之和
面试题 50 : 向下的路径节点值之和
面试题 51 : 节点值之和最大的路径
面试题 49 : 从根节点到叶节点的路径数字之和
题目:
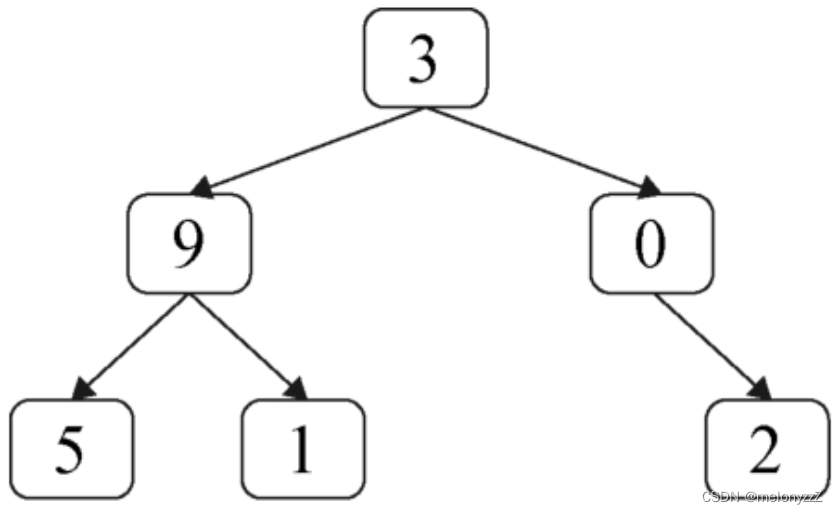
在一棵二叉树中所有节点都在 0~9 的范围之内,从根节点到叶节点的路径表示一个数字。求二叉树中所有路径表示的数字之和。例如,下图中的二叉树有 3 条从根节点到叶节点的路径,它们分别表示数字 395、391 和 302,这 3 个数字之和是 1088。
分析:
首先考虑如何计算路径表示的数字。顺着指向子节点的指针路径向下遍历二叉树,每到达一个节点,就相当于在路径表示的数字末尾添加一个数字。例如,在最开始到达根节点,此时路径表示数字 3(0 x 10 + 3 = 3)。然后到达节点 9,此时路径表示数字 39(3 x 10 + 9 = 39)。然后向下到达节点 5,此时路径表示数字 395(39 x 10 + 5 = 395)。
这就是说,每当遍历到一个节点时都计算从根节点到当前节点的路径表示的数字。如果这个节点还有子节点,就把这个值传下去继续遍历它的子节点。先计算到当前节点为止的路径表示的数字,再计算它的子节点的路径表示的数字,这实质上就是典型的二叉树前序遍历。
代码实现:
class Solution {
public:
int sumNumbers(TreeNode* root) {
if (root == nullptr)
return 0;
return dfs(root, 0);
}
private:
int dfs(TreeNode* root, int pathNum) {
pathNum = pathNum * 10 + root->val;
if (root->left == nullptr && root->right == nullptr)
return pathNum;
int sum = 0;
if (root->left)
sum += dfs(root->left, pathNum);
if (root->right)
sum += dfs(root->right, pathNum);
return sum;
}
};解题小经验:
与二叉树中路径相关的面试题很多,通常这些面试题都可以用深度优先搜索解决,很少采用广度优先搜索。这是因为路径通常顺着指向子节点的指针方向,也就是纵向方向,这更加符合深度优先搜索的特点。广度优先搜索是从左到右遍历每层的节点,是横向的遍历。因此深度优先搜索更加适合解决与路径相关的面试题。
面试题 50 : 向下的路径节点值之和
题目:
给定一棵二叉树和一个值 sum,求二叉树中节点值之和等于 sum 的路径的数目。路径的定义为二叉树中顺着指向子节点的指针向下移动所经过的节点,但不一定从根节点开始,也不一定到叶节点结束。例如,在下图所示的二叉树中有两条路径的节点值之和等于 8,其中第 1 条路径从节点 5 开始经过节点 2 到达节点 1,第 2 条从节点 2 开始到节点 6。
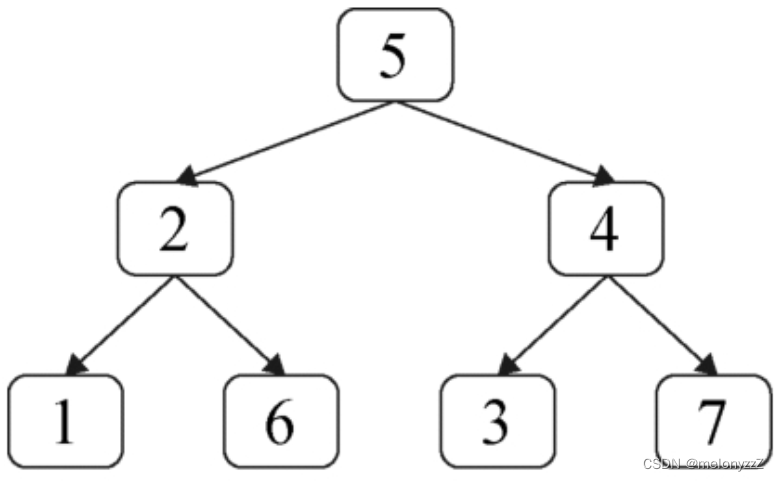
分析:
在这个题目中,二叉树的路径的定义发生了改变,它不一定从根节点开始,也不一定到叶节点结束。路径的起始节点的不确定性给计算路径经过的节点值之和带来了很大的困难。
虽然路径不一定从根节点开始,但仍然可以求得从根节点开始到达当前遍历节点的路径所经过的节点值之和。例如,从上图的二叉树的根节点 5 出发,一边顺着指向子节点的指针在路径上向下移动,一边累加当前已经经过的节点值之和。当到达节点 5 时,节点值之和为 5。假设先顺着指向左子节点的指针到达节点 2,此时路径经过的节点值之和为 7。如果再顺着指向右子节点的指针到达节点 6,此时路径经过的节点值之和为 15。
如果在路径上移动时把所有累加的节点值之和都保存下来,就容易知道是否存在从任意节点出发的值为给定 sum 的路径。
前缀和 + 哈希表。
例如,当到达上图中二叉树的根节点 5 时,从根节点开始的路径节点值之和是 5。当到达节点 2 时,从跟节点开始的路径经过的节点值之和是 7。当到节点 6 时,从根节点开始的路径经过的节点值之和为 13。由于要找出节点值之和为 8 的路径,而 13 与 5 的差值是 8,这就说明从节点 5 的下一个节点(即节点 2)开始到节点 6 结束的路径经过的节点值之和为 8。
有了前面的经验,就可以采用二叉树深度优先搜索来解决与路径相关的问题。当遍历到一个节点时,先累加从根节点开始的路径上的节点值之和,再计算它的左右子节点的路径的节点值之和。这就是典型的前序遍历的顺序。
代码实现:
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
if (root == nullptr)
return 0;
unordered_map<long, int> sumToCount;
sumToCount[0] = 1;
return dfs(root, targetSum, sumToCount, 0);
}
private:
int dfs(TreeNode* root, int targetSum,
unordered_map<long, int>& sumToCount, long sum)
{
sum += root->val;
int counts = sumToCount[sum - targetSum];
++sumToCount[sum];
if (root->left)
counts += dfs(root->left, targetSum, sumToCount, sum);
if (root->right)
counts += dfs(root->right, targetSum, sumToCount, sum);
--sumToCount[sum];
return counts;
}
};面试题 51 : 节点值之和最大的路径
题目:
在二叉树中将路径定义为顺着节点之间的连接从任意一个节点开始到达任意一个节点所经过的所有节点。路径中至少包含一个节点,不一定经过二叉树的根节点,也不一定经过叶节点。给定非空的一棵二叉树,请求出二叉树所有路径上节点值之和的最大值。例如,在下图所示的二叉树中,从节点 15 开始经过节点 20 到达节点 7 的路径的节点值之和为 42,是节点值之和最大的路径。

分析:
这个题目中二叉树路径的定义又和前面的不同。这里的路径最主要的特点是路径有可能同时经过一个节点的左右子节点。例如,在上图中,一条路径可以经过节点 15、节点 20 和节点 7,即节点 20 的左子节点 15 和右子节点 7 同时在一条路径上。当然,路径也可以不同时经过一个节点的左右子节点。例如,在上图中,一条路径可以经过节点 -9、节点 20、节点 15 和节点 -3。
值得注意的是,如果一条路径同时经过某个节点的左右子节点,那么该路径一定不能经过它的父节点。例如,在上图中,经过节点 20、节点 15、节点 7 的路径不能经过节点 -9。
也就是说,当路径到达某个节点时,该路径既可以前往它的左子树,也可以前往它的右子树。但如果路径同时经过它的左右子树,那么就不能经过它的父节点。
由于路径可能只经过左子树或右子树而不经过根节点,为了求得二叉树的路径上节点值之和的最大值,需要先求出左右子树中路径节点值之和的最大值(左右子树中的路径不经过当前节点),再求出经过根节点的路径节点值之和的最大值,最后对三者进行比较得到最大值。由于需要先求出左右子树的路径节点值之和的最大值,再求根节点,这看起来就是后序遍历。
基于二叉树的后序遍历的参考代码如下所示:
class Solution {
public:
int maxPathSum(TreeNode* root) {
maxSum = INT_MIN;
dfs(root);
return maxSum;
}
private:
int dfs(TreeNode* root) {
if (root == nullptr)
return 0;
int left = max(0, dfs(root->left));
int right = max(0, dfs(root->right));
maxSum = max(maxSum, root->val + left + right);
// 注意:如果一条路径同时经过某个节点的左右子节点,
// 那么该路径一定不能经过它的父节点
return root->val + max(left, right);
}
private:
int maxSum;
};二叉树的直径
题目:
给你一棵二叉树的根节点,返回该树的直径。
二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root。
两节点之间路径的长度由它们的边数表示。
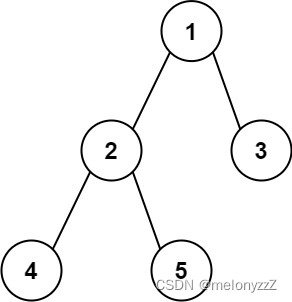
示例:
输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度代码实现:
class Solution { public: int diameterOfBinaryTree(TreeNode* root) { diameter = INT_MIN; dfs(root); return diameter; } private: int dfs(TreeNode* root) { if (root == nullptr) return -1; int left = dfs(root->left); int right = dfs(root->right); diameter = max(diameter, 2 + left + right); return 1 + max(left, right); } private: int diameter; };