1. 数值的整数次方

原题链接:

剑指 Offer 16. 数值的整数次方 - 力扣（LeetCode）https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/

我们都知道, 在C语言的一根库中有一个pow函数可以用来求一个数的乘方, 本题就是要求实现类似于pow的功能. 要求实现特定库函数(特别是处理数值和字符串的函数)的功能是一类常见的面试题。这就要求我们在平时编程的时候除了能熟练使用库函数,更重要的是要理解库函数的实现原理。

1.1 运行超时的思路

想必大家第一个想到的思路就是循环. 我们对输入的幂指数进行特殊处理: 使得幂指数大于0. 然后利用for循环将底数乘到最终结果上就可以了! 很遗憾Leetcode 并不想让你这么做, 面试官也不希望看到这种解法.

double myPow(double x, int n){
    //保存结果的变量
    double result = 1.0;
    //为啥用long int 后面讲
    long int a = n;
    //如果幂指数小于0, 取绝对值, 2的-1次方就等于二分之一的一次方嘛
    if(n < 0)
    {
        a = -a;
        x = 1 / x;
    }
    //循环将底数乘到结果上
    int i = 0;
    for(i = 0;i < a;i++)
    {
        result *= x;
    }
    return result;
}

1.2 思路一: 快速幂 (递归实现)

快速幂的本质就是分治, 大家细细品味哈.

以上方法不可行, 我们可以换一种思路考虑: 例如, 我们的目标是求出一个数字的32次方，如果我们已经知道了它的16次方，那么只要在16次方的基础上再平方一次就可以了。而16次方是8次方的平方。这样以此类推，我们求32次方只需要做5次乘法: 先求平方，在平方的基础上求4次方，在4次方的基础上求8次方，在8次方的基础上求16次方，最后在16次方的基础上求32次方。对于奇数次方, 我们只需要拿出一个底数出来即可.
也就是说，我们可以用如下公式求a 的n次方:

同上面一样我们需要对输入的幂指数进行处理:

将幂指数保存在一个变量, 例如 a 中, 当幂指数小于 0 时, 我们就令 a = -a, 底数x = 1 / x, 就相当于对幂指数取绝对值, 然后把幂指数的负号作用到底数上, 2 的 -1 次方就等于 1/2 的 1 次方嘛.

注意: 保存幂指数的变量必须选用存储范围更大的 long int, 我们都知道 int 的范围是

当我们输入的幂指数为 - (2的31次方时), 取绝对值后 int 类型是存不下这个数的.

解题的时间复杂度: O(logN), 因为是递归, 函数调用需要函数栈帧, 故空间复杂度: O(logN).


double recurison(double x, long int n)
{
    //递归的结束条件, 任何数的0次幂都等于1(0除外)
    if(n==0)
    {
        return 1;
    }
    // 将幂指数整除2, 但是我们选用位运算提高效率
    double result = recurison(x, n>>1);
    result *= result;
    //判断奇偶, 奇数就乘以一个底数, 同样使用位运算提高效率
    if((n&1)==1)
    {
        result*=x;
    }
    return result;
}

double myPow(double x, int n){
    double result;
    //对指数进行处理
    long int a = n;
    if(n < 0)
    {
        a = -a;
        x = 1 / x;
    }
    return recurison(x, a);
}

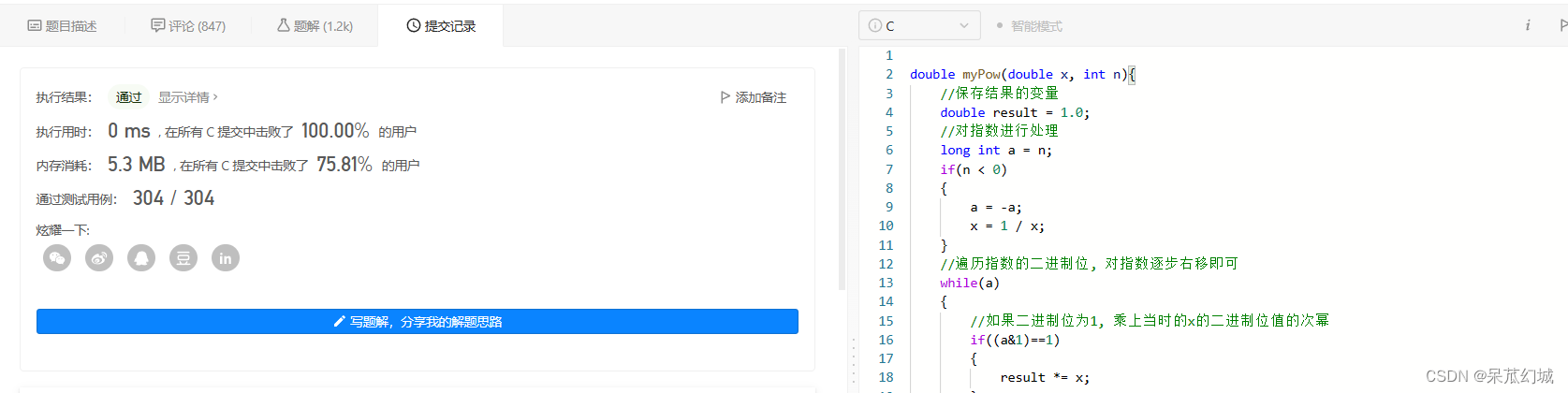
1.3 思路二: 快速幂 (迭代实现)

还是以具体的例子来看: 我们一开始还是对幂指数进行处理使它为整数哈, 当幂指数n为偶数, 例如x ^ 8 我们先算 x * x = x ^ 2, 再算x ^ 2 * x ^ 2 = x ^ 4, 最后算x ^ 4 * x ^ 4 = x ^ 8. 对于奇数呢, 我们将指数进行拆分, 例如 x ^ 10, 指数10 = 1 + 4 + 8 = 2 ^ 0 + 2 ^ 2 + 2 ^ 3, 即

x ^ 10 = x ^ 1 * x ^ 4 * x ^ 8

依次类推, 直到将幂指数的二进制遍历完毕, 显然result 乘上的值在每一遍历一个二进制位时都要逐步递增:

偶数自然不用说, 也是满足此规律的.


double myPow(double x, int n){
    //保存结果的变量
    double result = 1.0;
    //对指数进行处理
    long int a = n;
    if(n < 0)
    {
        a = -a;
        x = 1 / x;
    }
    //遍历指数的二进制位, 对指数逐步右移即可
    while(a)
    {
        //如果二进制位为1, 乘上当时的x的二进制位值的次幂
        if((a&1)==1)
        {
            result *= x;
        }
        //下一个二进制位的, x的二进制位值的次幂
        x = x * x;
        //将a右移
        a >>= 1;
    }
    return result;
}