【数据结构与算法】递归、回溯、八皇后 一文打尽！

news2025/1/21 18:44:20

 🎉🎉欢迎光临🎉🎉

🏅我是苏泽，一位对技术充满热情的探索者和分享者。🚀🚀

🌟特别推荐给大家我的最新专栏《数据结构与算法：初学者入门指南》📘📘

本专栏纯属为爱发电永久免费！！！

这是苏泽的个人主页可以看到我其他的内容哦👇👇

努力的苏泽icon-default.png?t=N7T8http://suzee.blog.csdn.net

目录

递归

引言：

第一部分：什么是递归算法？

第二部分：递归算法的基本原理

第三部分：递归算法的应用场景——一个小故事

第四部分：递归算法在开发中的应用和经典问题

在面试中，递归算法经常被用作考察候选人的问题解决能力和算法思维。以下是一些经典的使用递归的面试问题：

迷宫问题

代码的逻辑如下：

是否发现一个问题：

那就再进一步 到了回溯 最经典的八皇后问题

回溯：

思想：

方法：

八皇后：

优化思路：

我们可以用一维数组来表示这个皇后棋盘  arr[8]的八个值就是  八个皇后的横坐标 （因为我们已经知道他们不会同行，即纵坐标默认不相同）

具体步骤如下：

代码 实现：

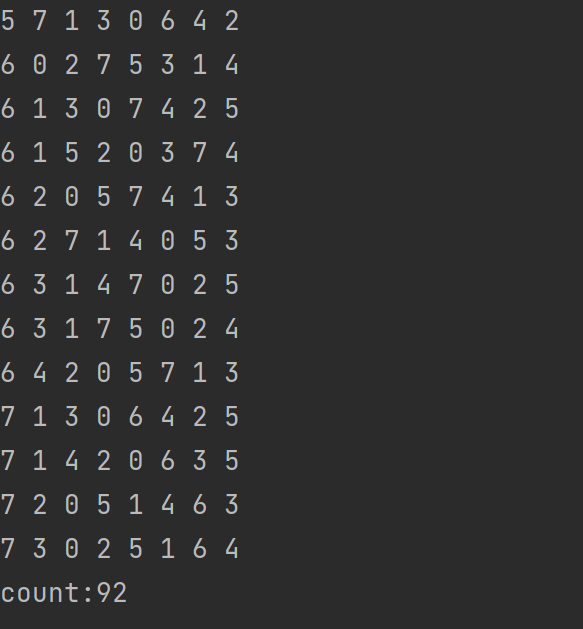
测试结果​

递归

引言：


递归算法是计算机科学中一种强大而又神秘的概念。它的简洁性和优雅性使得它在许多领域都得到广泛应用，例如数学、计算机科学和算法设计。本文将带你一起探索递归算法的精髓，解开其无限奥秘。

第一部分：什么是递归算法？


递归算法是一种自引用的算法，它通过将大问题分解为更小的相似子问题来解决复杂的计算任务。递归算法的核心思想在于将一个问题分解为一个或多个基本情况和一个或多个规模较小但同样结构的子问题。这些子问题将继续被分解，直到达到基本情况，然后逐层返回结果，最终解决原始问题。

第二部分：递归算法的基本原理

在使用递归算法时，我们需要明确两个关键要素：基本情况和递归关系。

  1. 基本情况：基本情况是指递归过程中的终止条件。当问题达到基本情况时，递归停止，直接返回结果。基本情况的定义必须确保问题规模足够小，可以直接求解。
  2. 递归关系：递归关系定义了如何将原始问题分解为规模较小但同样结构的子问题。通过递归关系，我们能够将问题逐步分解，并将子问题的解合并为原始问题的解。

第三部分：递归算法的应用场景——一个小故事

从前有座山山里有座庙，庙里有个小和尚。这个小和尚喜欢讲故事，有一天他开始讲了一个故事：“从前有座山山里有座庙，庙里有个小和尚，小和尚再说一个故事 故事的内容是...”

这个故事似乎永远没有结束的样子。听众们开始思考，这个故事是如何结束的呢？

递归的思想在这个故事中展现得淋漓尽致。小和尚讲的故事不断重复，每次故事的结尾都是开始的部分，形成了一个无限循环的过程。这种无限循环的特性正是递归的本质。

在这个故事中，小和尚讲的故事本身就是一个子问题，而每个子问题又以同样的方式继续展开，不断地迭代下去。

第四部分：递归算法在开发中的应用和经典问题

递归算法在开发中有广泛的应用。它可以用来解决各种问题，包括但不限于以下情况：

  • 树和图的遍历：递归算法可以应用于树和图的深度优先搜索（DFS）和广度优先搜索（BFS）等遍历算法。
  • 排列和组合：递归算法可以生成所有可能的排列和组合，如全排列、子集生成等。
  • 分治算法：递归算法可以将一个大问题分解为多个子问题，并将子问题的解合并为整体解，如归并排序、快速排序等。
  • 动态规划：递归算法可以用于解决动态规划问题，通过将问题分解为子问题，并保存子问题的解，避免重复计算，提高效率。

在面试中，递归算法经常被用作考察候选人的问题解决能力和算法思维。以下是一些经典的使用递归的面试问题：

  • 阶乘计算：使用递归算法计算给定数的阶乘。
  • 斐波那契数列：使用递归算法生成斐波那契数列的第n项。
  • 二叉树相关问题：如二叉树的遍历、判断是否为二叉搜索树等。
  • 字符串处理：如字符串反转、判断回文串等。

第五部分：用Java实现递归
下面是一个简单的Java代码示例，用于计算给定数的阶乘：

public class RecursionExample {
    public static int factorial(int n) {
        // 基本情况：当n为0或1时，直接返回1
        if (n == 0 || n == 1) {
            return 1;
        }
        // 递归关系：将问题分解为规模较小的子问题
        return n * factorial(n - 1);
    }

    public static void main(String[] args) {
        int number = 5;
        int result = factorial(number);
        System.out.println("Factorial of " + number + " is: " + result);
    }
}

这个比较简单 那我们就继续引入一个较为复杂一点的案例

迷宫问题

迷宫问题是一个经典的应用递归思想的例子。它通常描述为在一个二维的迷宫中，从起点到达终点的路径规划问题。现在我们来说明如何通过递归来分析和解决迷宫问题。

  1. 问题分析：

    • 首先，我们需要明确问题的输入和输出。在迷宫问题中，输入是一个迷宫地图，包含起点、终点以及障碍物的位置信息。输出是一条从起点到终点的路径，或者判断是否存在可行路径。
    • 其次，我们要考虑如何表示迷宫和路径。通常我们可以使用二维数组或矩阵表示迷宫，其中不可通过的区域可以用特定的符号或数字表示。路径可以用一个列表或栈来保存经过的位置。
    • 最后，我们需要定义问题的规模和边界条件。规模是指迷宫的大小，边界条件是指起点和终点的位置是否在合法范围内。

  2. 解决问题：

    • 首先，我们要确定递归函数的定义和结束条件。在迷宫问题中，可以定义一个递归函数来搜索路径，每次尝试从当前位置向上下左右四个方向移动，直到达到终点或无法继续移动为止。
    • 接下来，我们需要考虑递归函数的递归关系。在迷宫问题中，递归关系可以描述为：如果当前位置可通过且未被访问过，则将当前位置标记为已访问，并尝试向四个方向递归搜索路径。
    • 最后，我们要处理递归函数的返回值。如果找到一条路径，则返回该路径；如果无法找到路径，则返回空值或特定的标识。

我们先把这个迷宫用二维数组画出来：

// 先创建一个二维数组，模拟迷宫
		// 地图
		int[][] map = new int[8][7];
		// 使用1 表示墙
		// 上下全部置为1
		for (int i = 0; i < 7; i++) {
			map[0][i] = 1;
			map[7][i] = 1;
		}

		// 左右全部置为1
		for (int i = 0; i < 8; i++) {
			map[i][0] = 1;
			map[i][6] = 1;
		}
		//设置挡板, 1 表示
		map[3][1] = 1;
		map[3][2] = 1;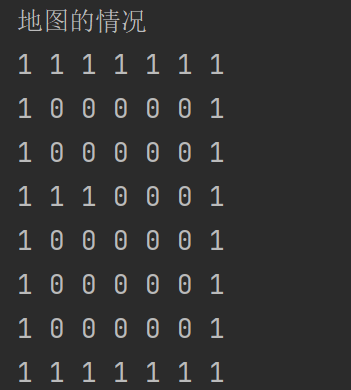

/**
	 * 
	 * @param map 表示地图
	 * @param i 从哪个位置开始找
	 * @param j 
	 * @return 如果找到通路，就返回true, 否则返回false
	 */
	public static boolean setWay(int[][] map, int i, int j) {
		if(map[6][5] == 2) { // 通路已经找到ok
			return true;
		} else {
			if(map[i][j] == 0) { //如果当前这个点还没有走过
				//按照策略 下->右->上->左  走
				map[i][j] = 2; // 假定该点是可以走通.
				if(setWay(map, i+1, j)) {//向下走
					return true;
				} else if (setWay(map, i, j+1)) { //向右走
					return true;
				} else if (setWay(map, i-1, j)) { //向上
					return true;
				} else if (setWay(map, i, j-1)){ // 向左走
					return true;
				} else {
					//说明该点是走不通，是死路
					map[i][j] = 3;
					return false;
				}
			} else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
				return false;
			}
		}
	}

代码的逻辑如下：

  1. 首先检查当前位置 (i, j) 是否为目标位置 (6, 5)，如果是，说明已经找到通路，返回 true。
  2. 如果当前位置不是目标位置，那么再判断当前位置是否可走（map[i][j] == 0）。如果是可走的，继续执行下面的步骤；否则返回 false。
  3. 将当前位置标记为已经走过（map[i][j] = 2）。
  4. 依据下、右、上、左的顺序，依次尝试向四个方向移动。
    • 如果向下移动 (setWay(map, i+1, j)) 返回 true，说明找到了通路，直接返回 true。
    • 如果向右移动 (setWay(map, i, j+1)) 返回 true，说明找到了通路，直接返回 true。
    • 如果向上移动 (setWay(map, i-1, j)) 返回 true，说明找到了通路，直接返回 true。
    • 如果向左移动 (setWay(map, i, j-1)) 返回 true，说明找到了通路，直接返回 true。
  5. 如果以上四个方向都没有找到通路，说明该点是走不通的，将该位置标记为死路（map[i][j] = 3），并返回 false。
  6. 如果当前位置不可走（map[i][j] != 0），直接返回 false。

整个算法通过递归的方式，在每个位置上尝试四个方向的移动，直到找到通路或者所有路径都被尝试完毕。如果找到通路，返回 true，否则返回 false。在每次递归调用时，都会改变地图的状态，标记已经走过的路径，以及死路。

是否发现一个问题：

这个代码只按照了其中一种策略（即下 右 上 左的策略）  这样出来的路径就不一定是最短的  如果需要优化就要用到后面的贪心算法 到时候会专门出一期贪心算法的讲解。

但是这里我们要讲解的是这个递归的思路 可以非常简洁的解决了问题

那就再进一步 到了回溯 最经典的八皇后问题

回溯：

思想：

回溯是一种经典的算法思想，常用于解决在给定的搜索空间中找到所有可能解的问题。它的基本思想是通过尝试不同的选择，当发现当前选择并不是有效的解决方案时，回溯到上一步并尝试其他选择，直到找到所有的解或者确定不存在解。

方法：

  1. 定义问题的解空间：确定问题的解可以表示为一棵树的结构，每个节点代表一个可能的解，通过在树上进行深度优先搜索来遍历所有可能的解。

  2. 定义候选集：确定每个节点的子节点是什么。候选集表示在当前节点上可以进行选择的所有可能选项。

  3. 编写递归函数：递归函数负责遍历解空间树。在每个节点上，递归函数检查当前节点是否是一个有效解决方案，如果是，则将其添加到结果集中。然后，递归地调用自身来继续探索下一个节点。

  4. 定义结束条件：在递归函数中，定义结束条件来判断是否到达了解空间的叶子节点或满足特定条件的节点。当满足结束条件时，递归函数停止递归，回溯到上一步进行其他选择。

  5. 回溯：在递归函数中，当发现当前选择不是有效解决方案时，需要回溯到上一步并尝试其他选择。回溯是通过撤销对当前节点的选择，恢复到上一步状态，并继续遍历其他可能的选择

八皇后：

八皇后问题是一个经典的组合问题，其目标是在一个8×8的棋盘上放置8个皇后，使得任意两个皇后都不能互相攻击，即不能在同一行、同一列或同一对角线上。

解决八皇后问题的思路如下：

  1. 定义问题的解空间：在每一行放置一个皇后，每个皇后的位置可以表示为一个二维坐标 (row, col)，其中 row 表示行数，col 表示列数。因为每一行只能放置一个皇后，所以解空间可以看作是一个排列问题。

  2. 定义候选集：候选集表示每个节点上可以进行选择的所有可能选项。对于每一行，皇后可以放置在该行的任意列上，所以候选集为 [0, 7]，表示列的范围。

  3. 编写递归函数：递归函数负责遍历解空间树。在每个节点上，递归函数检查当前节点的选择是否满足不攻击的条件，如果是，则将其添加到结果集中。然后，递归地调用自身来继续探索下一行的选择。

  4. 定义结束条件：在递归函数中，定义结束条件来判断是否已经放置了所有的皇后。当所有的皇后都被放置时，递归函数停止递归，回溯到上一行进行其他选择。

  5. 回溯：在递归函数中，当发现当前选择不满足不攻击的条件时，需要回溯到上一列并尝试其他选择。回溯是通过撤销对当前节点的选择，恢复到上一步状态，并继续遍历其他可能的选择。

优化思路：

我们可以用一维数组来表示这个皇后棋盘  arr[8]的八个值就是  八个皇后的横坐标 （因为我们已经知道他们不会同行，即纵坐标默认不相同）

  1. 定义问题的解空间：使用一个一维数组 arr，其中 arr[i] 表示第 i 行皇后的列位置。因为每一行只能放置一个皇后，所以解空间可以看作是一个排列问题。

  2. 定义候选集：候选集表示每个节点上可以进行选择的所有可能选项。对于每一行，皇后可以放置在该行的任意列上，所以候选集为 [0, 7]，表示列的范围。

  3. 编写递归函数：递归函数负责遍历解空间树。在每个节点上，递归函数检查当前节点的选择是否满足不攻击的条件，如果是，则将其添加到结果集中。然后，递归地调用自身来继续探索下一行的选择。

  4. 定义结束条件：在递归函数中，定义结束条件来判断是否已经放置了所有的皇后。当所有的皇后都被放置时，递归函数停止递归，回溯到上一行进行其他选择。

  5. 回溯：在递归函数中，当发现当前选择不满足不攻击的条件时，需要回溯到上一列并尝试其他选择。回溯是通过撤销对当前节点的选择，恢复到上一步状态，并继续遍历其他可能的选择。

具体步骤如下：

  1. 初始化一个长度为 8 的一维数组 arr，将其所有元素初始化为 0

  2. 从第一行开始逐行放置皇后，调用递归函数 backtrack(arr, 0)，其中第二个参数表示当前放置的行数。

  3. 在递归函数 backtrack 中，首先判断是否已经放置了所有的皇后（即当前行数等于总行数），如果是，则将 arr 添加到结果集中。

  4. 否则，遍历当前行的所有列，依次尝试放置皇后。对于每个位置，判断是否与已经放置的皇后冲突，如果不冲突，则将该位置记录到 arr 中，然后递归调用 backtrack(arr, row + 1) 进行下一行的放置。

  5. 在回溯过程中，要记得撤销对当前节点的选择，即将 arr[row] 的值恢复为 -1，以便尝试其他选择。

  6. 最终，返回结果集，即所有满足条件的皇后位置组合。

代码 实现：

public class Queue8 {
    static int MaxSize=8;
    static int[] arr=new int[MaxSize];
    static int count =0;
    public static void main(String[] args) {
        check(0);
        System.out.println("count:"+count);
    }

    /**
     *description<放置第n个皇后>

         * @param n 第n个皇后
         * @return void
         * @author SUZE
         * @time 2024/2/18-18:56
         */

    public static void check(int n){
        if (n==8){//每当n为8意味着已经放置了8个皇后了,因为其实0~7才是需要检验的
            printf();
            count++;
            return;
        }
        for (int i=0;i<MaxSize;i++){
            //先把第n个皇后 放在该行的第i列
            arr[n]=i;
            if (judge(arr,n)){
            check(n+1);//满足了则继续下一位
            }
        }

    }
/**
 *description<功能描述>
        [arr, i, n] 放置前n个皇后有无冲突
     * @return boolean
     * @author SUZE
     * @time 2024/2/18-18:57
     */

    public static boolean judge(int[] arr,int n) {
        for (int i=0;i<n;i++){
            // 同列皇后情况   两皇后处在斜线的情况 （即纵坐标之差等于横坐标之差 因为可能包含了四个象限所以用绝对值）
            if (arr[i]==arr[n]||Math.abs(arr[i]-arr[n])==Math.abs(i-n)){
                return false;
            }
        }
        return true;
    }

    public static void printf(){
        for (int i=0;i<MaxSize;i++){
            System.out.printf("%d ",arr[i]);
        }
        System.out.println();
    }

}

测试结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1454886.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

个性签名大全

个性签名大全

只许一生浮世清欢愿我以孤独作为铠甲&#xff0c;自此不再受伤愿我是阳光&#xff0c;明媚而不忧伤我不敢太勇敢太执着太骄傲&#xff0c;我怕失去开始你是我的天使&#xff0c;最后你是我的唯一姐的霸气&#xff0c;无人能比&#xff0c;哥的傲气&#xff0c;无人能朋唯有万事…
阅读更多...
03_uartLinux内核模块

03_uartLinux内核模块

01_basicLinux内核模块-CSDN博客文章浏览阅读23次。环境IDubuntuMakefilemodules:clean:basic.creturn 0;运行效果。https://blog.csdn.net/m0_37132481/article/details/136157384?csdn_share_tail%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%…
阅读更多...
技术再被认可，Smartbi荣获“2023大数据产业年度创新技术突破”奖

技术再被认可，Smartbi荣获“2023大数据产业年度创新技术突破”奖

近日&#xff0c;由金猿、数据猿、上海大数据联盟主办&#xff0c;上海市经济和信息化委员会、上海科学技术委员会指导的“第六届金猿季&魔方论坛——大数据产业发展论坛”在上海举行。 思迈特软件凭借“基于数据模型的自然语言数据查询系统“荣获“2023大数据产业年度创新…
阅读更多...
MATLAB | 绘图复刻(十五) | 环形聚类树状图

MATLAB | 绘图复刻(十五) | 环形聚类树状图

本期复刻效果&#xff1a; 感觉出的聚类分析树状图绘制工具也不少了&#xff0c;未来可能会统一整理为一个工具包&#xff1f;(任重道远&#xff0c;道阻且长)&#xff1a; 代码讲解 0 数据设置 写了比较多的注释应该比较易懂&#xff1a; clc; clear; close all% 样品起名s…
阅读更多...
2024年【安全员-C证】报名考试及安全员-C证考试资料

2024年【安全员-C证】报名考试及安全员-C证考试资料

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 安全员-C证报名考试参考答案及安全员-C证考试试题解析是安全生产模拟考试一点通题库老师及安全员-C证操作证已考过的学员汇总&#xff0c;相对有效帮助安全员-C证考试资料学员顺利通过考试。 1、【多选题】《工伤保险…
阅读更多...
吴恩达机器学习全课程笔记第二篇

吴恩达机器学习全课程笔记第二篇

目录 前言 P31-P33 logistics &#xff08;逻辑&#xff09;回归 决策边界 P34-P36 逻辑回归的代价函数 梯度下降的实现 P37-P41 过拟合问题 正则化代价函数 正则化线性回归 正则化logistics回归 前言 这是吴恩达机器学习笔记的第二篇&#xff0c;第一篇笔记请见&…
阅读更多...
SSH密钥认证登陆流程(Vscode连接到远程)

SSH密钥认证登陆流程(Vscode连接到远程)

目录 前言连接远程步骤1. 下载工具包wsCli到本地机器2. 本地机器上生成ssh密钥3. 在服务器上安装公钥4. vscode连接到远程 参考资料 前言 SSH&#xff08;Secure Shell&#xff09;是一种用于远程登录和安全传输数据的网络协议。它提供了两种主要的远程连接方式&#xff1a; 密…
阅读更多...
字符设备驱动分步注册实现LED驱动的编写

字符设备驱动分步注册实现LED驱动的编写

头文件 #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t;#define RCC 0x50000A28 #define LED1_ADDR 0x50006000 #defi…
阅读更多...
Unity求物体关于平面镜像对称后坐标以及旋转

Unity求物体关于平面镜像对称后坐标以及旋转

前言&#xff1a;如题&#xff0c;我在已知一个平面L和物体A&#xff0c;我希望得到镜像后的物体B的位置和旋转。 效果&#xff1a; 推导&#xff1a; 首先我们需要知道物体的对称坐标A&#xff0c;我们现在能已知A坐标以及平面L的法线&#xff0c;如果我们能得到B的坐标&…
阅读更多...
芯品荟｜吉他屏驱应用介绍

芯品荟｜吉他屏驱应用介绍

PART ONE 市场简介 - Market Profile - 古典吉他与小提琴、钢琴并列为世界著名三大乐器。 目前&#xff0c;带屏成为吉他产品的新发展趋势。 核心应用 调音器、节拍器、录音器、效果、练习、循环乐段。 特色应用 4.3寸以下TFT屏 分辨率800*480以下 不带音弦按键替代&…
阅读更多...
java项目的构建流程

java项目的构建流程

1.创建项目 2.创建模块 创建时要注意组ID的命名 通常包含以下模块: 项目的pom文件中,依赖如下(web模块不需要依赖,也不需要main文件夹): 3.配置pom文件 1),主pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://mav…
阅读更多...
2.18通过字符设备驱动分步注册过程实现LED驱动的编写，编写应用程序测试

2.18通过字符设备驱动分步注册过程实现LED驱动的编写，编写应用程序测试

应用程序&#xff1a; #include<stdlib.h> #include<stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include<unistd.h> #include<string.h> #include<sys/ioctl.h> #include"myled.h&quo…
阅读更多...
ubuntu22.04-磁盘管理-虚拟机动态扩容-系统monitor

ubuntu22.04-磁盘管理-虚拟机动态扩容-系统monitor

文章目录 1.虚拟机2.ubuntu设置3.命令查看4.系统资源管理器1.虚拟机 关闭ubuntu22.04，然后修改虚拟机设置，如下图所示： 修改容量 2.ubuntu设置 搜索打开disks，如下图所示： 选择目标磁盘，选择调整大小到目标大小即可。
阅读更多...
vmware-17虚拟机安装教程及版本密钥（保姆级，包含图文讲解，不需注册账户）

vmware-17虚拟机安装教程及版本密钥（保姆级，包含图文讲解，不需注册账户）

文章目录 vmware安装教程一、下载vmware二、安装三、破解密匙 vmware安装教程 一、下载vmware 1.进入VMware官网&#xff1a;https://www.vmware.com/sg/products/workstation-pro.html 2.向下翻找到&#xff0c;如下界面并点击“现在安装” 3.稍事等待以下直到出现以下界面…
阅读更多...
医疗器械企业融资排行榜，敷尔佳、心脉医疗、安杰思医学、西山科技、康诺思腾融资总额超70亿元！

医疗器械企业融资排行榜，敷尔佳、心脉医疗、安杰思医学、西山科技、康诺思腾融资总额超70亿元！

21世纪以来&#xff0c;中国医疗器械市场经历多年高速增长&#xff0c;产业集聚度、全球化发展进程不断提升&#xff0c;医疗器械行业竞争加剧。对于医疗器械新兴企业而言&#xff0c;获得融资不仅是支持其技术创新和产品研发生产的重要资金来源&#xff0c;更是推动企业扩张发…
阅读更多...
怎么恢复电脑重装前的数据？介绍几种有效的方法

怎么恢复电脑重装前的数据？介绍几种有效的方法

在日常生活和工作中&#xff0c;电脑已成为我们不可或缺的工具。然而&#xff0c;有时候我们会遇到一些突发情况&#xff0c;比如电脑系统崩溃需要重新安装系统。在这个过程中&#xff0c;我们可能会失去一些重要的数据&#xff0c;比如照片、文档、视频等。这些数据可能包含着…
阅读更多...
YOLOv8改进 | Conv篇 | 利用FasterBlock二次创新C2f提出一种全新的结构（全网独家首发，参数量下降70W）

YOLOv8改进 | Conv篇 | 利用FasterBlock二次创新C2f提出一种全新的结构（全网独家首发，参数量下降70W）

一、本文介绍 本文给大家带来的改进机制是利用FasterNet的FasterBlock改进特征提取网络，将其用来改进ResNet网络，其旨在提高计算速度而不牺牲准确性，特别是在视觉任务中。它通过一种称为部分卷积（PConv）的新技术来减少冗余计算和内存访问。这种方法使得FasterNet在多种设…
阅读更多...
速看！2024年泰国国际电力能源展10月16-18日

速看！2024年泰国国际电力能源展10月16-18日

2024年泰国&#xff08;亚洲&#xff09;国际电力能源展暨电工技术设备展 展会时间&#xff1a;2024年10月16-18日 展会地点&#xff1a;泰国.曼谷BITEC会展中心 主办单位&#xff1a;新加坡Fireworks展览集团 组织单位&#xff1a;武汉柏翰展览有限公司(Fireworks China) …
阅读更多...
vue框架-vue-cli

vue框架-vue-cli

vue-cli Vue CLI是一个官方的脚手架工具，用于快速搭建基于Vue.js的项目。Vue CLI提供了一整套可配置的脚手架，可以帮助开发人员快速构建现代化的Web应用程序。 Vue CLI通过提供预先配置好的Webpack模板和插件，使得开发人员可以在不需要手动编写Webpack配置的情况下快速创建…
阅读更多...
15.一种坍缩式的简单——组合模式详解

15.一种坍缩式的简单——组合模式详解

当曾经的孩子们慢慢步入社会才知道&#xff0c;那年味渐淡的春节就像是疾驰在人生路上的暂停键。 它允许你在隆隆的鞭炮声中静下心来&#xff0c;瞻前顾后&#xff0c;怅然若失。 也允许你在寂静的街道上屏气凝神&#xff0c;倾听自己胸腔里的那团人声鼎沸。 孩子们会明白的&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023