目录
前言
P31-P33
logistics (逻辑)回归
决策边界
P34-P36
逻辑回归的代价函数
梯度下降的实现
P37-P41
过拟合问题
正则化代价函数
正则化线性回归
正则化logistics回归
前言
这是吴恩达机器学习笔记的第二篇,第一篇笔记请见:
吴恩达机器学习全课程笔记第一篇
完整的课程链接如下:
吴恩达机器学习教程(bilibili)
推荐网站:
scikit-learn中文社区
吴恩达机器学习学习资料(github)
P31-P33
logistics (逻辑)回归
二进制分类问题

分类问题不适合使用线性回归算法,如下图所示,如果只有下面的四个良性和上面的四个恶性样本,那么画出的曲线可能是蓝色那条,此时可以设置一个阈值0.5,如果算出的值小于0.5,那么预测为良性,否则就为恶性
但是当右侧多了一个恶性样本之后,曲线可能就会变为绿色那条,此时选择0.5阈值就会导致大量的数据分类错误
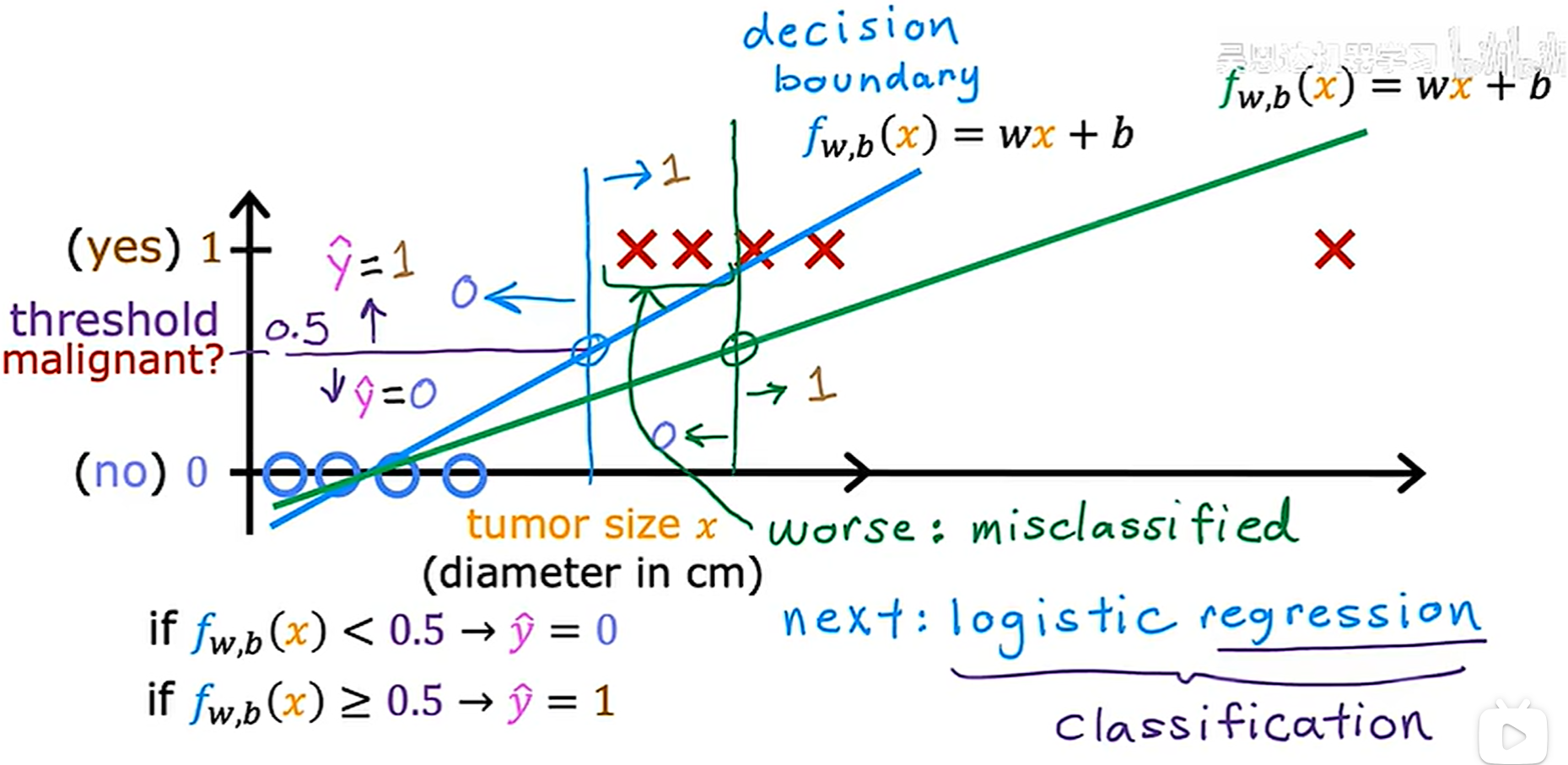
对于这种二进制分类问题,常用的是logistics回归,需要注意的是,虽然名称为“回归”,但这个算法是用于分类的
S型函数(英语:sigmoid function,或称乙状函数)是一种函数,因其函数图像形状像字母S得名。其形状曲线至少有2个焦点,也叫“二焦点曲线函数”。S型函数是有界、可微的实函数,在实数范围内均有取值,且导数恒为非负[1],有且只有一个拐点。S型函数和S型曲线指的是同一事物
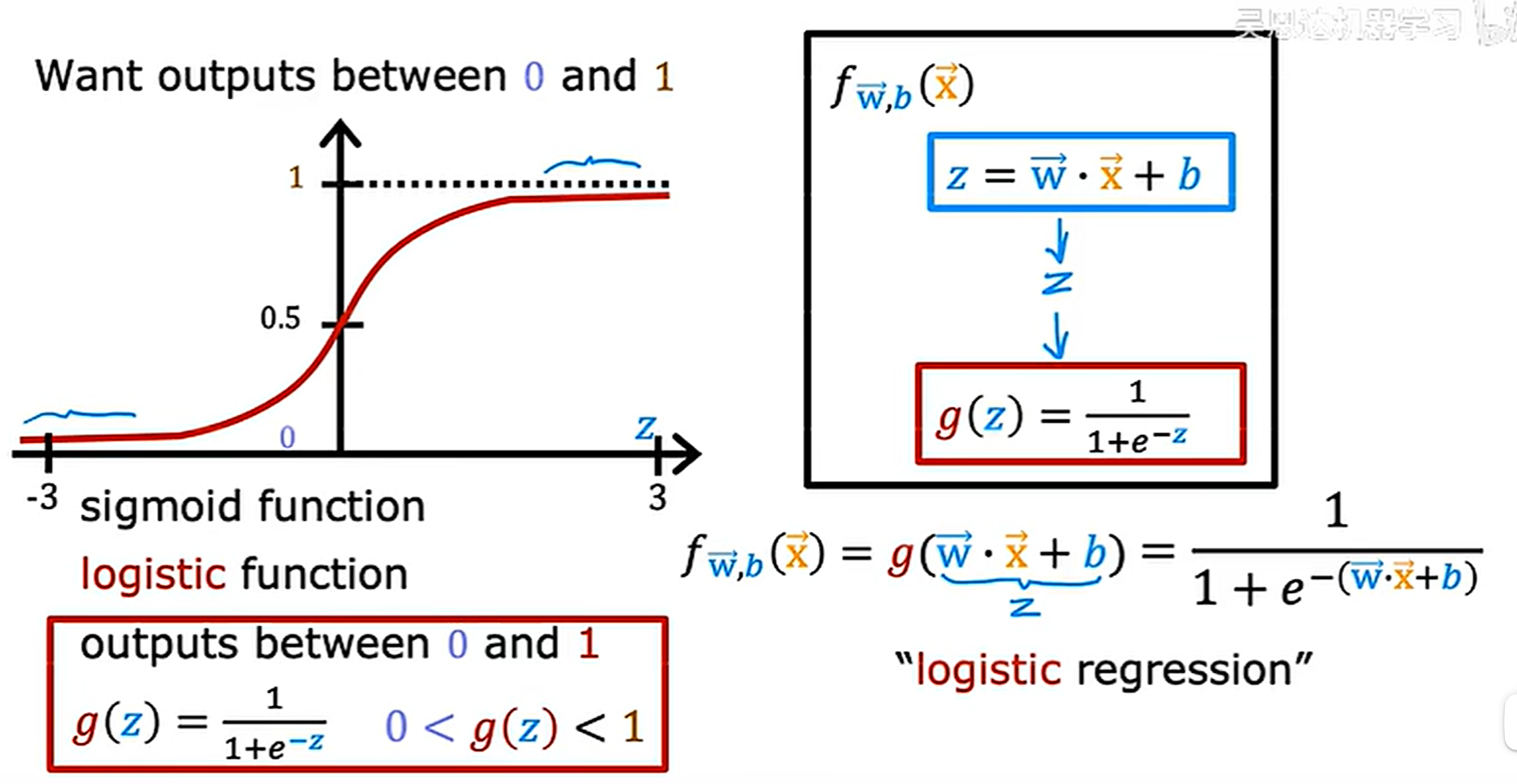
如上图所示,把sigmoid函数和原来的线性回归式子结合,使得最终结果永远落在0-1上,这样的话,最终预测的结果就可以被解释为被分类为1的概率

决策边界
二进制分类毕竟只有两种结果的可能性,要么是0,要么是1,即使logistics回归给出了为1的概率,也需要去设置一个阈值去决定最终的输出结果
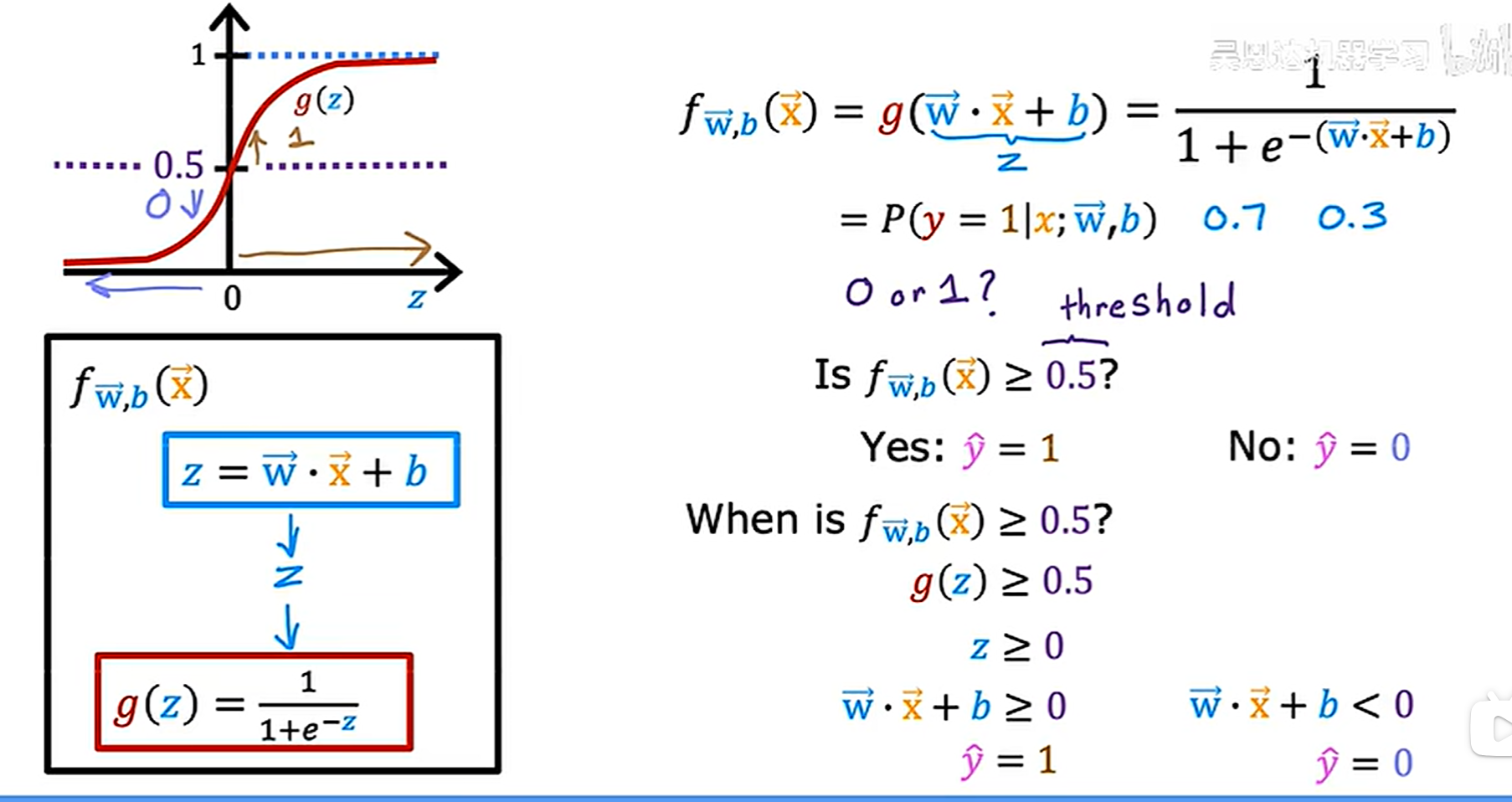
决策边界的可视化表示:
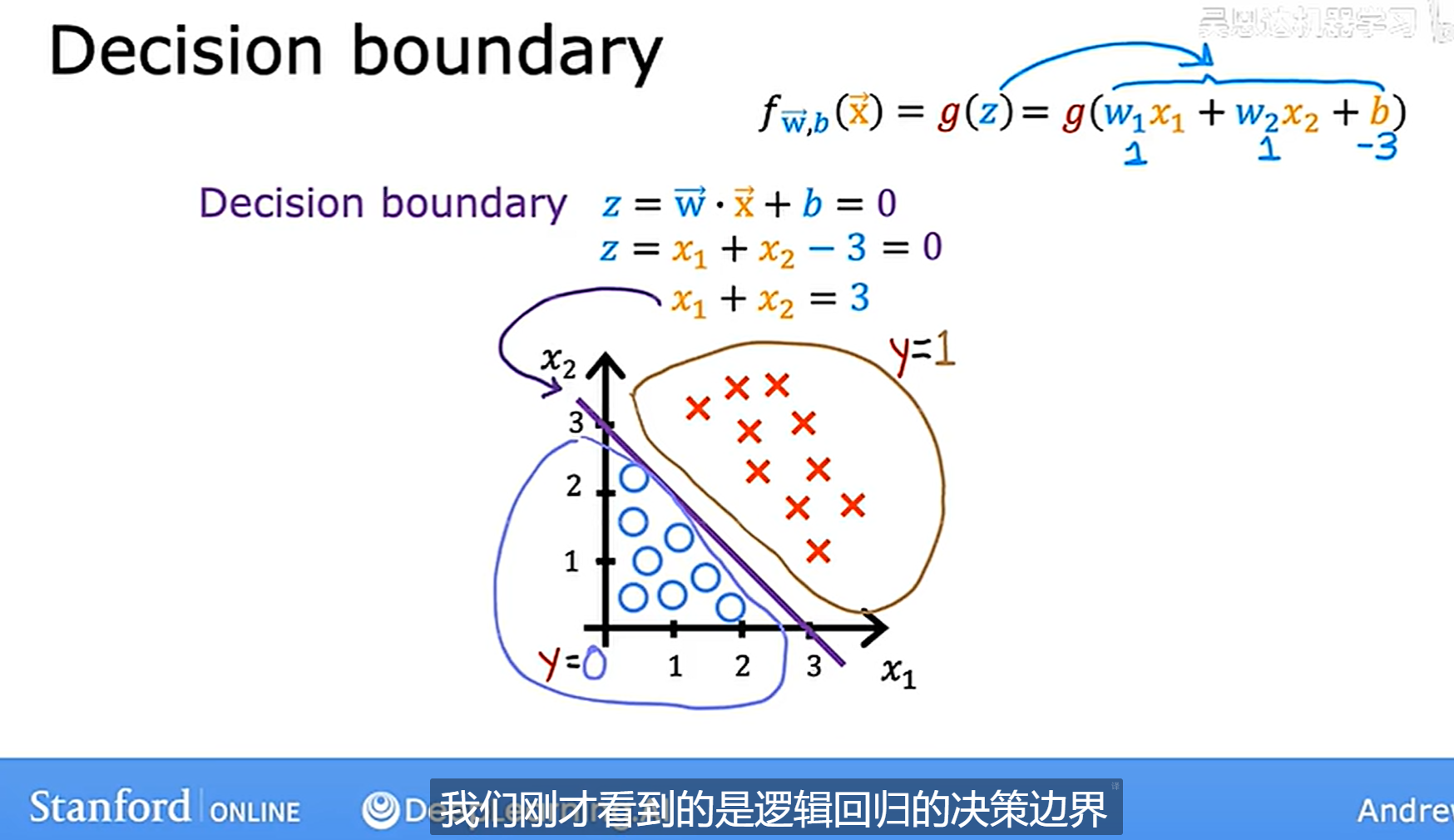
再看一种更复杂的情况,如果决策边界不是一条直线,可以使用之前学过的多项式回归去设置z的表达式,此时再令z值为0,得到决策边界如下:

P34-P36
逻辑回归的代价函数
对于平方误差成本函数,如果使用在线性回归上面,得到的曲线就是一个凸函数(convex),然而当使用在logistics回归上面,得到的就不是一个凸函数,此时运行梯度下降,就可能会陷入很多局部最小值
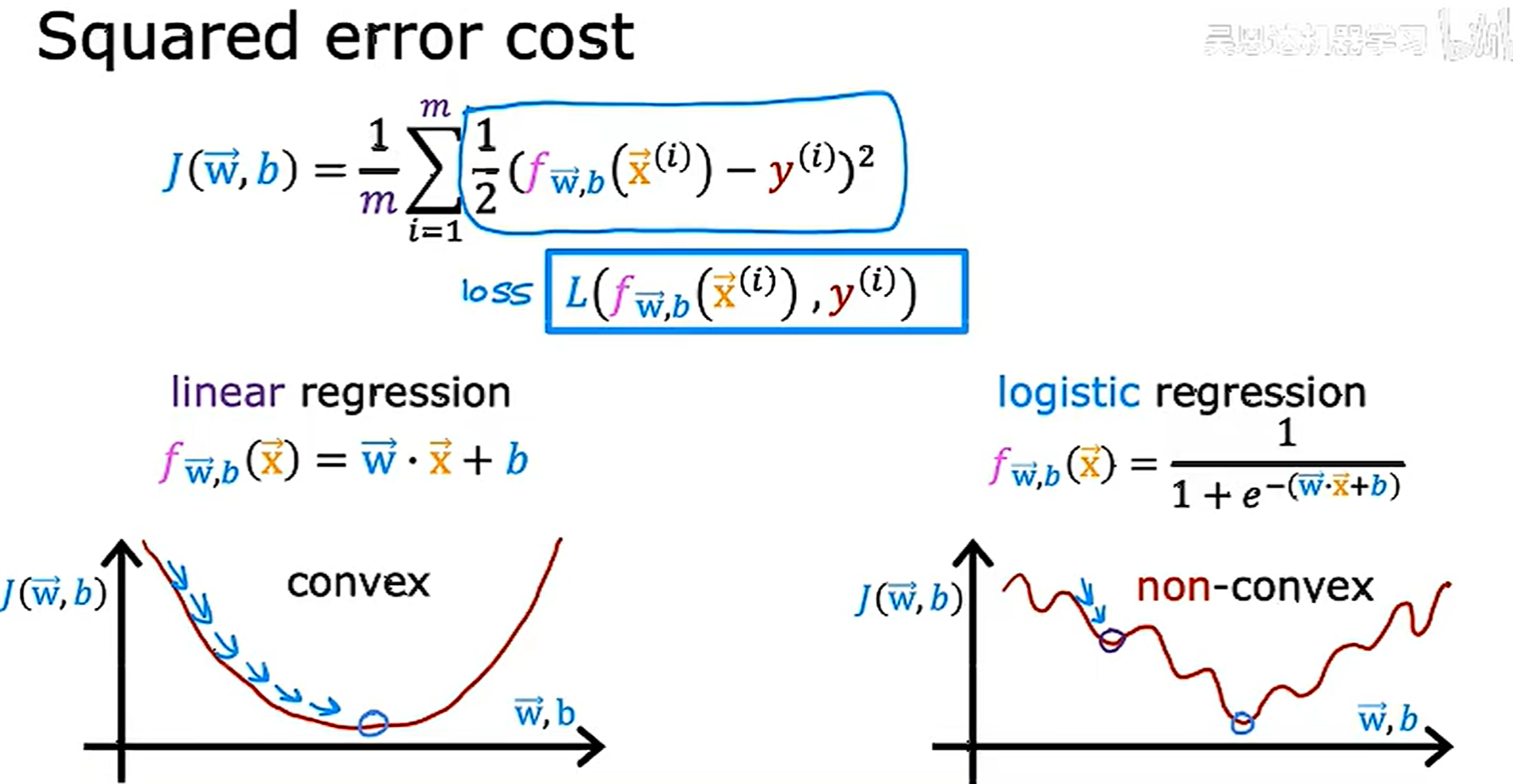
此时我们需要再找到一个新的代价函数,使得最后得到的结果是一个凸函数,如下图所示

如果真实的标签为1,那么图像如下,此时当预测值接近1,loss接近0,反之预测值接近0,loss接近无穷
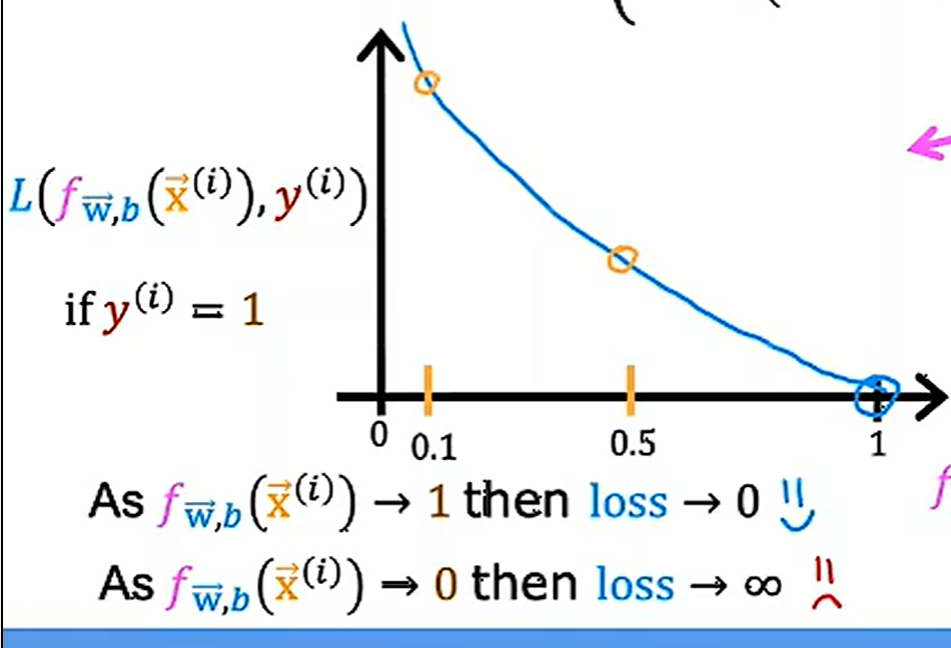
当真实标签为0时,同理
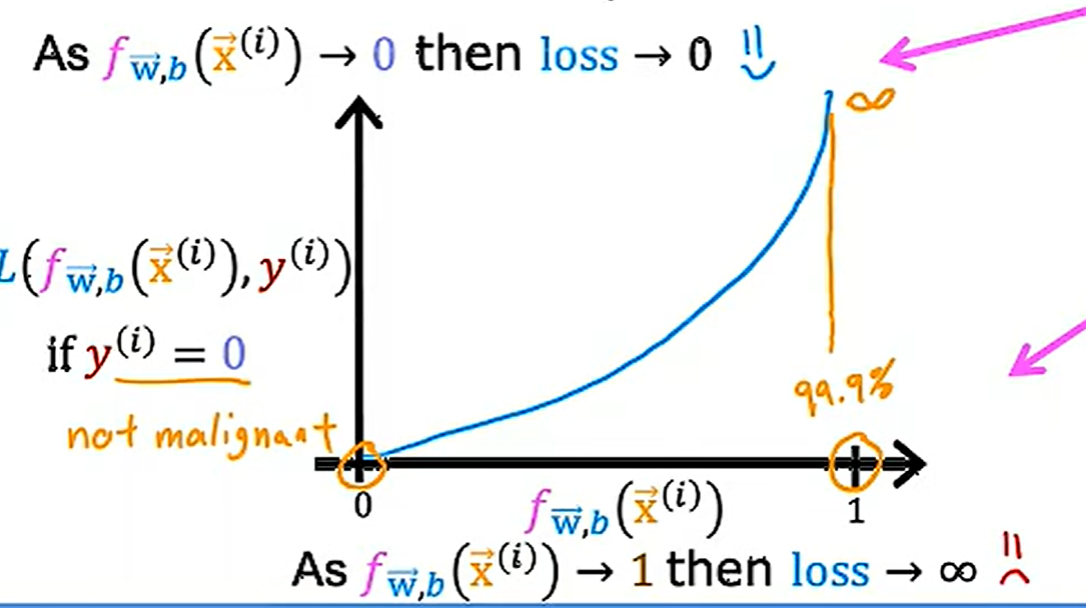
证明最后的代价函数时凸函数超出了本课程的范围
由于y的值只能是1或者0,所以可以把上面的loss function进行简化:
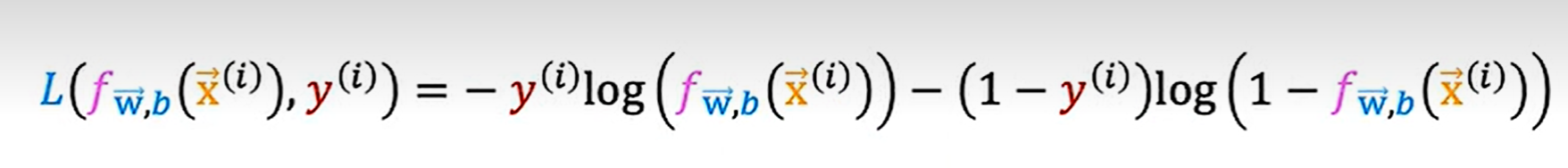
这个并不是完整的代价函数,我们对其进行进一步处理,最终得到:

梯度下降的实现
我们需要找到合适的w,b对logistics回归模型参数的拟合,我们依然使用梯度下降实现这一点
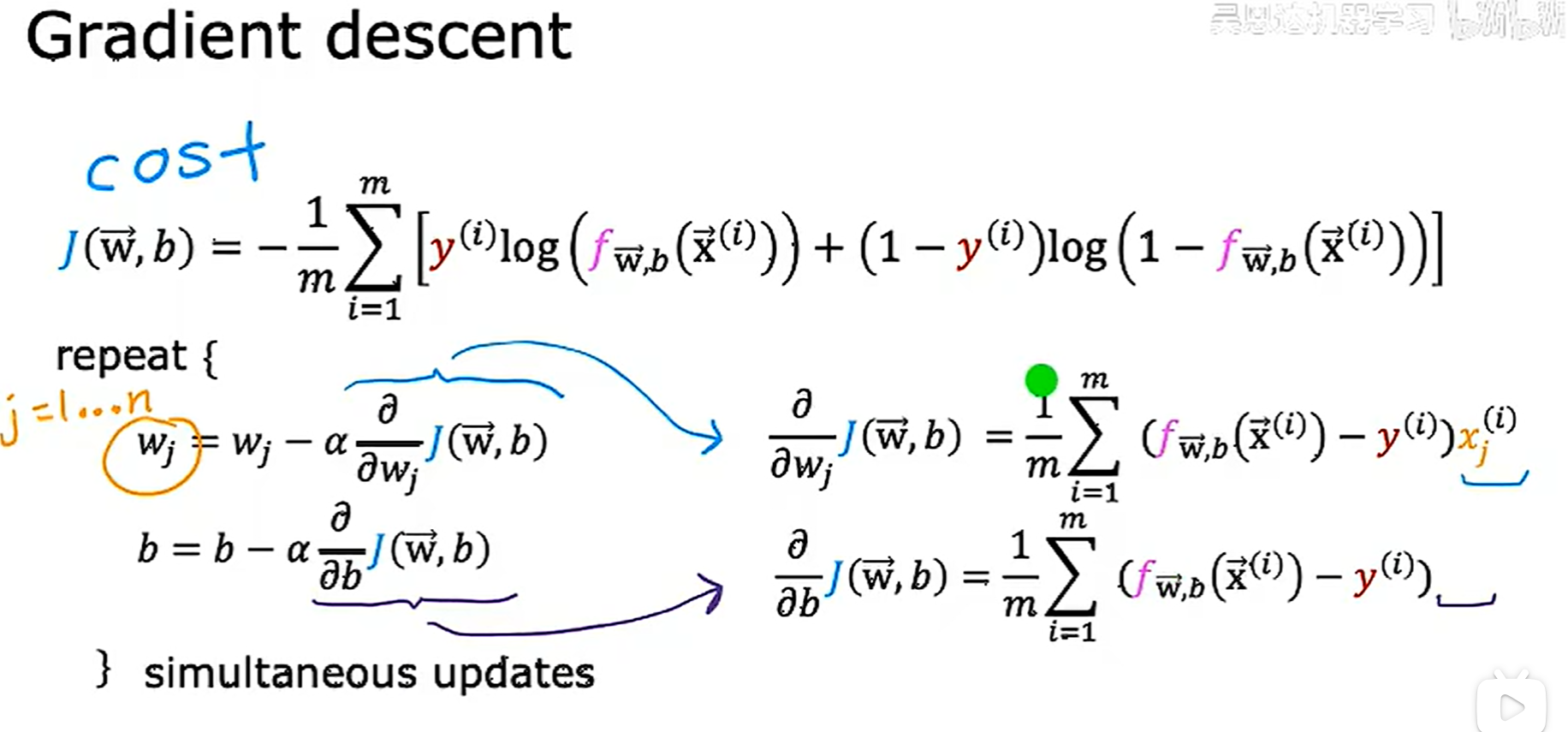
代入之后得到如下结果,可以发现似乎更新的算法和线性回归是相同的,但实际上f的定义发生了变化,最后,和线性回归一样,我们可以对logistics的梯度下降进行学习率的检测、向量化的实现以及进行特征缩放的处理

P37-P41
过拟合问题
在统计学中,过拟合(英语:overfitting,或称拟合过度)是指过于紧密或精确地匹配特定数据集,以致于无法良好地拟合其他数据或预测未来的观察结果的现象
回归过拟合的例子
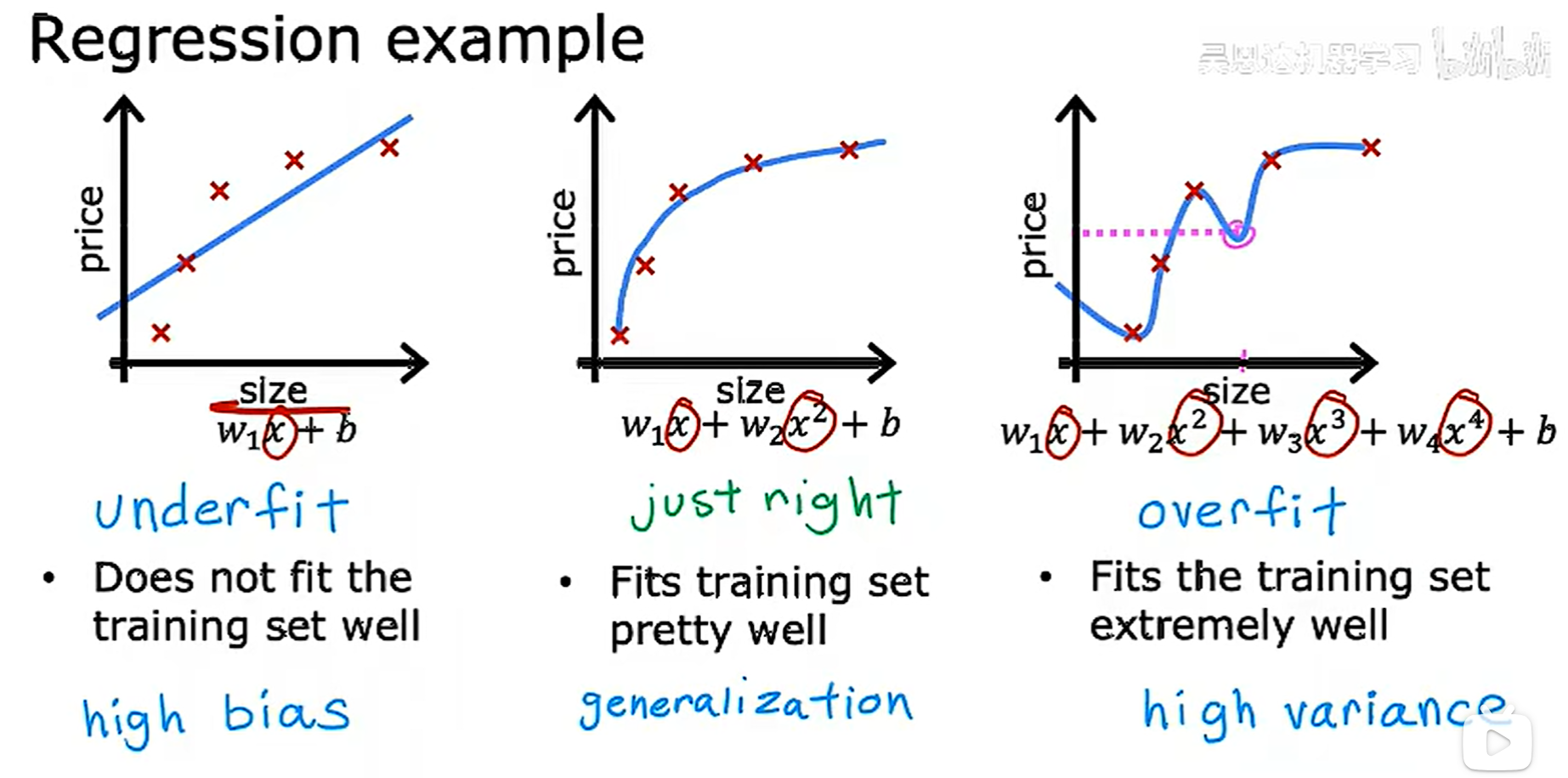
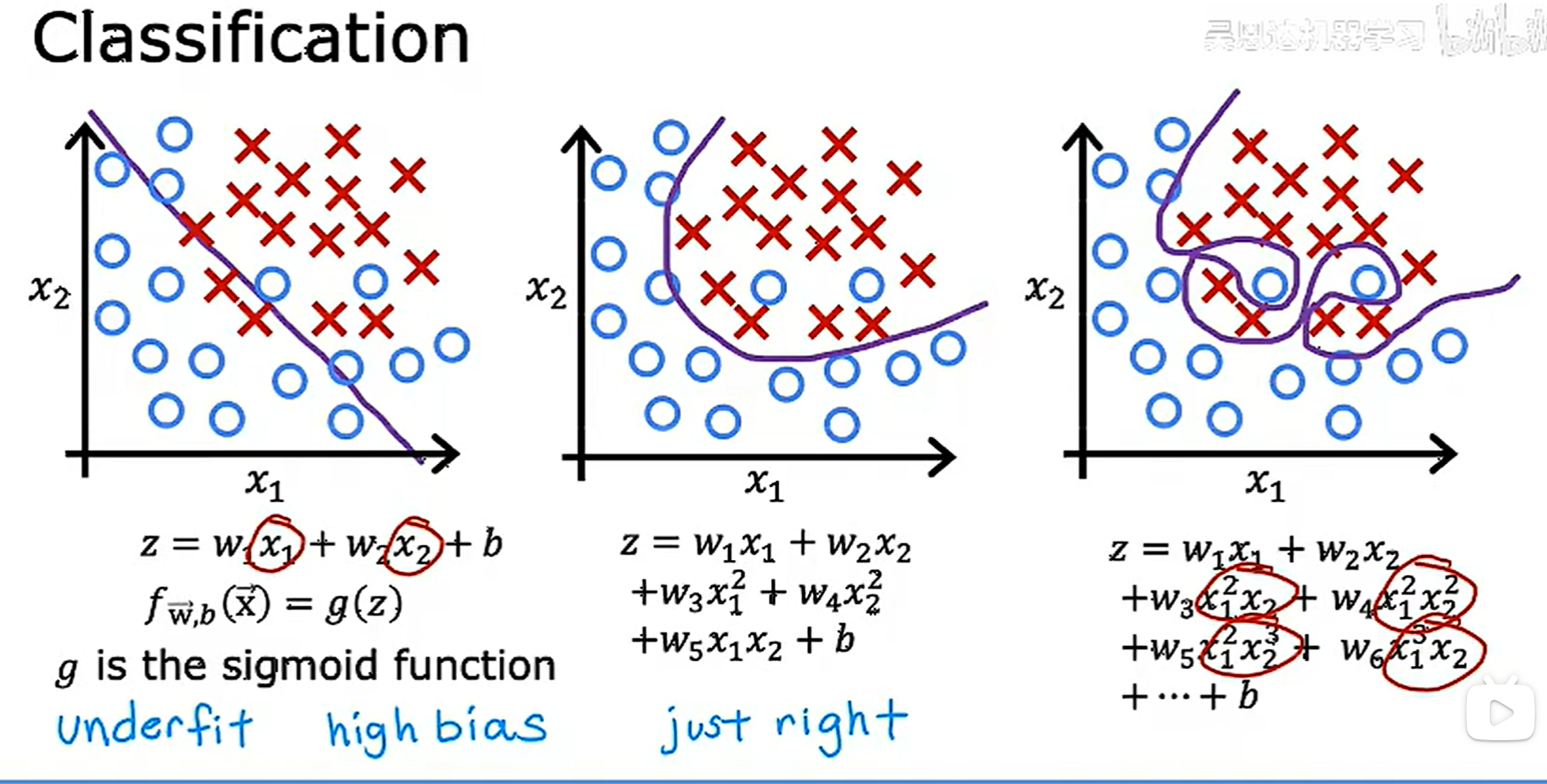
分类过拟合的例子
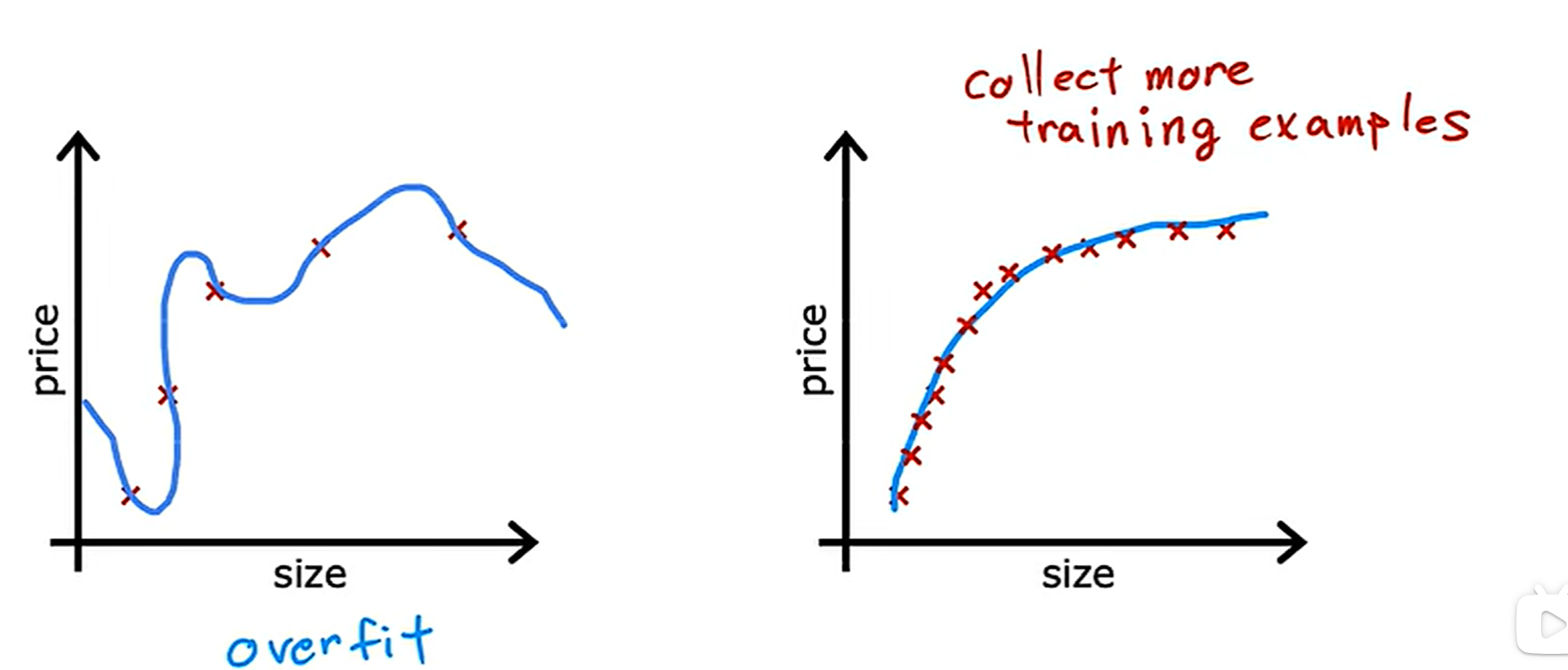
解决过拟合的第一个方法是去收集更多的数据
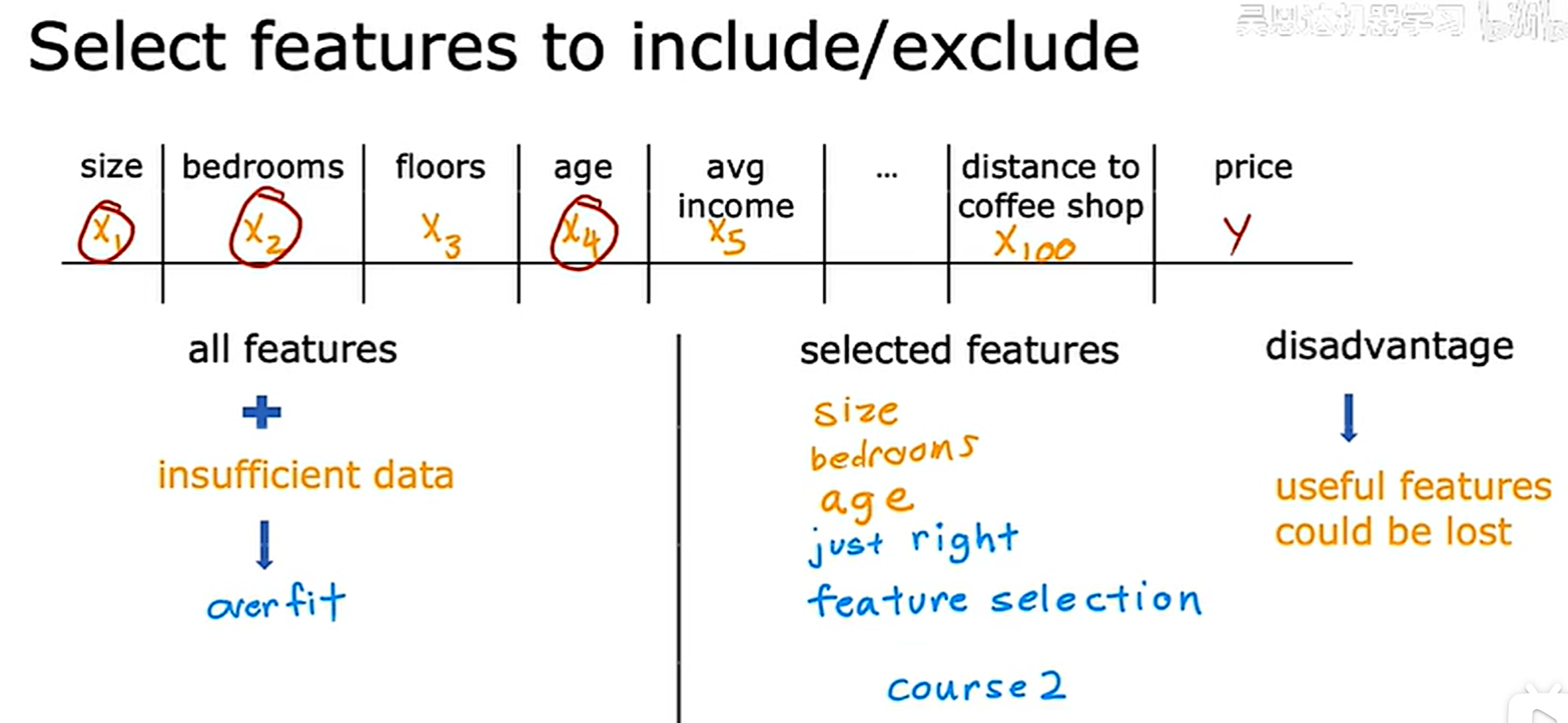
第二个方法是取选择合适的特征,而不是选择过多的特征,特别是当数据量不够时
当然这种方法的缺点就包括了可能会丢失一些对于预测数据很有用的信息
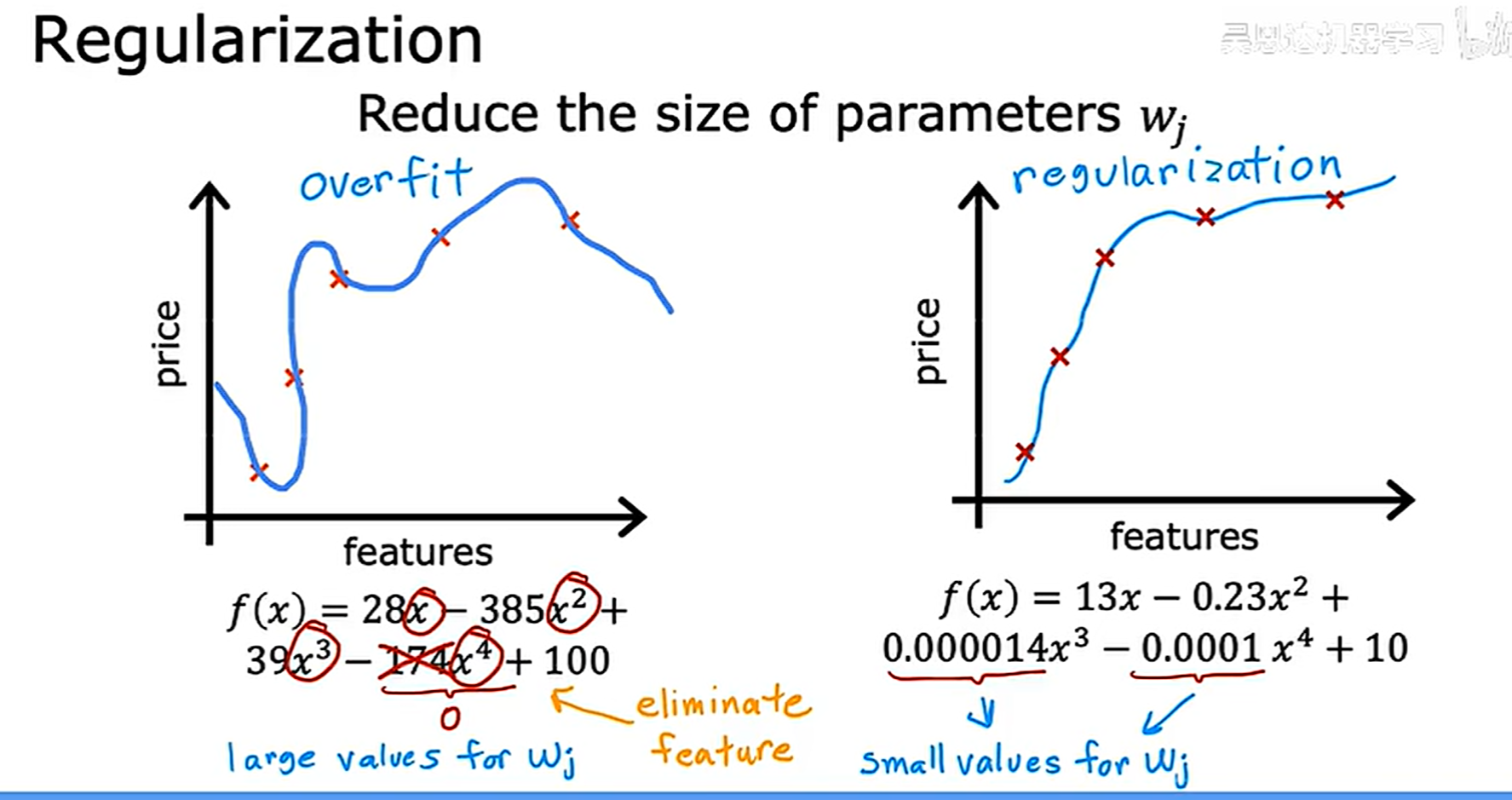
最后一种方法是正则化,这种方法可以减小一些参数的大小,这些参数对应的特征一般对整体影响较大,比如下面的右图,x的幂越高,就让其对应的参数变小
正则化代价函数
正则化的想法是,让参数有更小的值,使其不容易发生过拟合,但很多时候我们不知道应该减小哪些特征对应的参数,这时候就可以对所有的参数进行处理
一般只需要正则化参数而无需对b进行处理
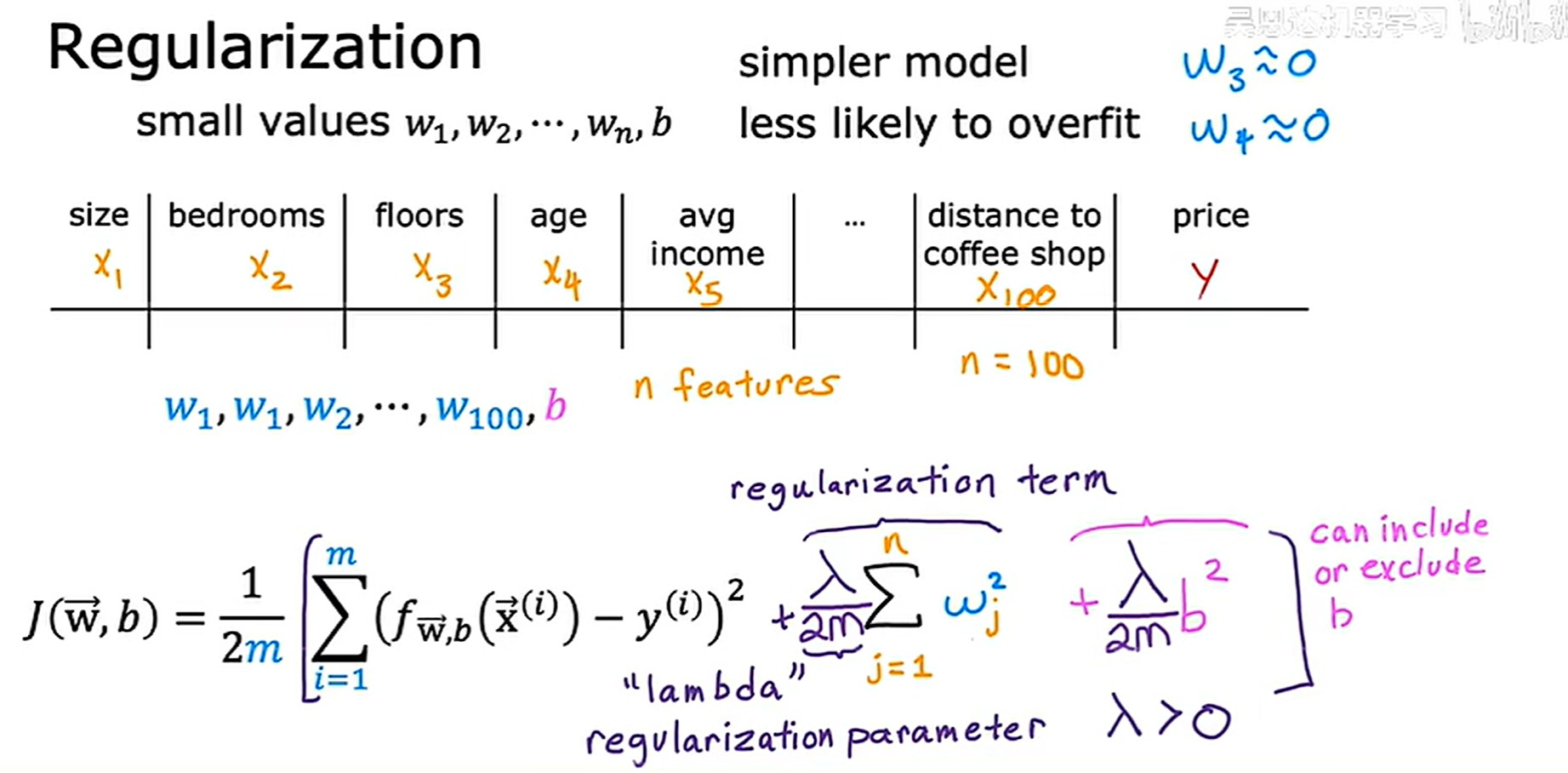
对于正则化参数的选择,一个极端是设置其值为0,此时就失去了意义,另一个极端是选择其值极大,此时,由于需要保证成本函数去最低值,就需要保证
的所有值都非常接近0

如上图所示,如果λ取0,就会发生过拟合,但若λ取很大,会使最后的曲线接近f(x)=b
正则化线性回归
实现正则化线性回归的梯度下降:


通过上图,可以发现正则化前后的梯度下降每一步的变化
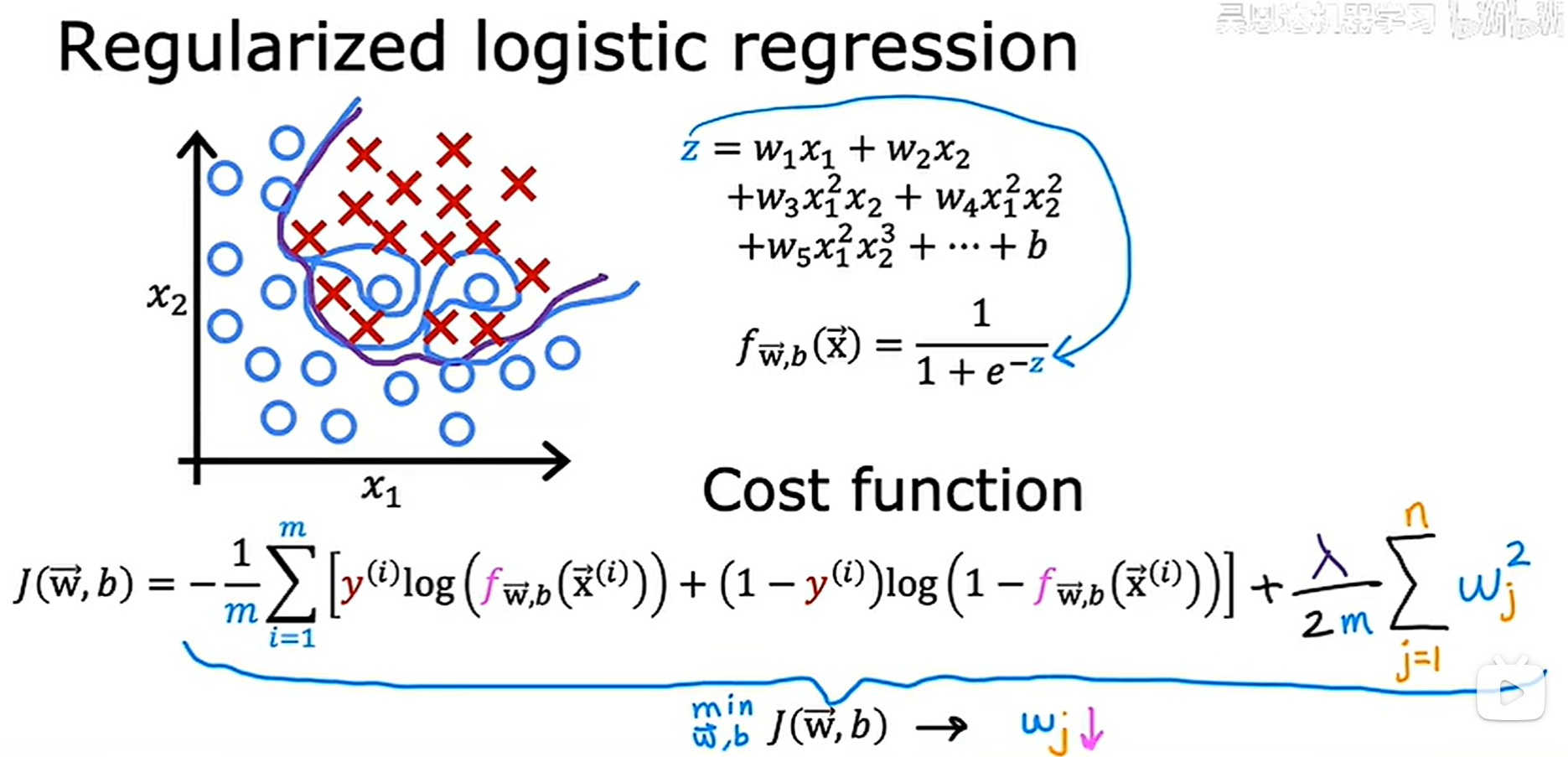
正则化logistics回归
如果使用多项式回归代入sigmoid函数可能会形成蓝色这条过拟合曲线,所以使用正则化去减小ω的值,从而让曲线变成紫色这条合适的曲线