1.题目

给定 $n$ 对正整数$ai$,$bi$，对于每对数，求出一组 $xi$,$yi$，使其满足 $ai\times xi+bi\times yi=gcd(ai,bi)$。

输入格式
第一行包含整数 $n$。

接下来 $n$ 行，每行包含两个整数 $ai$,$bi$。

输出格式
输出共 $n$ 行，对于每组 $ai$,$bi$，求出一组满足条件的 $xi$,$yi$，每组结果占一行。

本题答案不唯一，输出任意满足条件的 $xi$,$yi$ 均可。

数据范围
$1\le n\le 10^5,$

$1\le ai,bi\le 2\times 10^9$

输入样例：

2
4 6
8 18

输出样例：

-1 1
-2 1

2.基本思想

欧几里得算法

• 欧几里得算法（gcd）又称辗转相除法，是求最大公约数的一种方法。
• 代码实现：

public static long gcd(long m, long n) {//时间复杂度：O（log n）
        return n == 0 ? m : gcd(n, m % n);
    }

• lcm算法
  两个整数的最小公倍数与最大公因数之间有如下的关系：
  

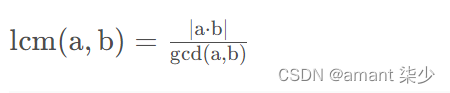
• 代码实现：

public static long lcm(long a, long b) {
        return a * b / gcd(a, b);
    }

裴蜀（贝祖）等式

• 对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）
  ax+by=m有整数解时当且仅当m是d的倍数。
  裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用扩展欧几里得算法（Extended Euclidean algorithm）求得。
• 方程12x+42y=6有解
• 特别地，方程 ax+by=1有整数解当且仅当整数a和b互素

扩展欧几里得算法
扩展欧几里得算法就是在求a，b的最大公约数d=gcd（a，b）的同时，求出贝祖等式ax+by=m的一个解（x0，y0）
如何递推？

x=y1
y=x1 - a / b * y1
通解：
x = x0 +（b / gcd ）* t       所有的x对b同模
y = y0 -（ a / gcd ）* t       所有的y对a同模

如果想要得到×大于0的第一个解？

b /= d；x =（x0 % b + b ）% b

---

gcd(a,b)
return b==0?a
我们观察到：欧几里德算法停止的状态是： a’= gcd ， b’ = 0 ，(a’,b’是递归最后一层时参数的值)那么，这是否能给我们求解 x y 提供一种思路呢？
a’x + b’y = gcd 此时x=1,y为任意数
因为，这时候，只要 a = gcd 的系数是 1 ，那么只要 b 的系数是 0 或者其他值
（无所谓是多少，反正任何数乘以 0 都等于 0 但是a 的系数一定要是 1），这时，我们就会有： a’*1 + b’*0 = gcd

当然这是最终状态，但是我们是否可以从最终状态反推到最初的状态呢？

假设当前我们要处理的是求出 a 和 b的最大公约数，并求出 x 和 y 使得
 a*x + b*y= gcd    ……(1)，--->要求的
而我们已经求出了下一个状态：b 和 a%b 的最大公约数，并且求出了一组x1 和y1 使得：
 b*x1 + (a%b)*y1 = gcd (2) ，-->下一个状态
那么这两个相邻的状态之间是否存在一种关系呢？

a%b = k  ==>  a = b*(a/b) +k  "/"舍掉余数的除法 ==> k=a-(a/b)*b
我们知道： a%b = a - (a/b)*b（这里的 “/” 指的是整除，例如 5/2=2 , 1/3=0），那么，我们可以进一步得到：

    gcd = b*x1 + (a-(a/b)*b)*y1

        = b*x1 + a*y1 – (a/b)*b*y1

        = a*y1 + b*(x1 – a/b*y1)        ……(3)

对比之前我们的状态,式(3)和式(1)：求一组 x 和 y 使得：a*x + b*y = gcd ，是否发现了什么？

这里：

    x = y1

    y = x1 – a/b*y1

这就是递推式,注意x,y是递归过程中的上一层,x1,y1是下一层(下一个状态)得到的值

3.代码实现

import java.util.Scanner;

public class Main {
    static int x, y;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        while (n-- > 0) {
            int a = sc.nextInt(), b = sc.nextInt();
            exgcd(a, b);
            System.out.println(x + " " + y);
        }
    }

    private static int exgcd(int a, int b) {
        if (b == 0) {//到达递归边界开始向上一层返回
            x = 1;
            y = 0;
            return a;
        }
        int d = exgcd(b, a % b);//保存最大公约数
        int x1 = x;//备份x1
        x = y;
        y = x1 - a / b * y;
        return d;
    }
}